【图像处理】快速傅里叶变换FFT MATLAB
FFT快速傅里叶变换介绍
当初学习FFT的时候就一直觉得这玩意真的是天才的创造。
我们知道DFT的公式:
X [ k ] = ∑ n = 0 N − 1 x [ n ] e − j 2 π N k n X[k]=\sum_{n=0}^{N-1}x[n]e^{-j\frac{2\pi}{N}kn} X[k]=n=0∑N−1x[n]e−jN2πkn
为了方便后续推到,我们一般假设 N = 2 μ N=2^{\mu } N=2μ
上述公式可以拆分成左边的奇数部分和右边的偶数部分.
X [ k ] = ∑ m = 0 N 2 − 1 x [ 2 m ] e − j 2 π N k 2 m + ∑ m = 0 N 2 − 1 x [ 2 m + 1 ] e − j 2 π N k ( 2 m + 1 ) = ∑ m = 0 N 2 − 1 x [ 2 m ] e − j 2 π k m N 2 + e − j 2 π k n N ∑ m = 0 N 2 − 1 x [ 2 m + 1 ] e − j 2 π k m N 2 X[k]=\sum_{m=0}^{\frac{N}{2}-1}x[2m]e^{-j\frac{2\pi}{N}k2m}+\sum_{m=0}^{\frac{N}{2}-1}x[2m+1]e^{-j\frac{2\pi}{N}k(2m+1)}\\ =\sum_{m=0}^{\frac{N}{2}-1}x[2m]e^{-j\frac{2\pi km}{\frac{N}2}}+e^{-j\frac{2\pi kn}{N}}\sum_{m=0}^{\frac{N}{2}-1}x[2m+1]e^{-j\frac{2\pi km}{\frac{N}2}}\\ X[k]=m=0∑2N−1x[2m]e−jN2πk2m+m=0∑2N−1x[2m+1]e−jN2πk(2m+1)=m=0∑2N−1x[2m]e−j2N2πkm+e−jN2πknm=0∑2N−1x[2m+1]e−j2N2πkm
将奇数部分和偶数部分分别记为 X e v e n [ k ] Xeven[k] Xeven[k]和 X o d d [ k ] Xodd[k] Xodd[k]得到
X [ k ] = X e [ k ] + e − j 2 π k n N X o [ k ] X e v e n [ k ] = ∑ m = 0 N 2 − 1 x [ 2 m ] e − j 2 π k m N 2 X o d d [ k ] = ∑ m = 0 N 2 − 1 x [ 2 m + 1 ] e − j 2 π k m N 2 k = 0 , 1 , . . . , N − 1 X[k]=Xe[k]+e^{-j\frac{2\pi kn}{N}}Xo[k]\\ Xeven[k]=\sum_{m=0}^{\frac{N}{2}-1}x[2m]e^{-j\frac{2\pi km}{\frac{N}2}}\\ Xodd[k]=\sum_{m=0}^{\frac{N}{2}-1}x[2m+1]e^{-j\frac{2\pi km}{\frac{N}2}}\\ k=0,1,...,N-1 X[k]=Xe[k]+e−jN2πknXo[k]Xeven[k]=m=0∑2N−1x[2m]e−j2N2πkmXodd[k]=m=0∑2N−1x[2m+1]e−j2N2πkmk=0,1,...,N−1
其中 k = 0 , 1 , . . . , N − 1 k=0,1,...,N-1 k=0,1,...,N−1对于每个k,有:
C ( k ) = C ( M u l t i f l i c a t i o n , A d d i t i o n ) = ( 1 , 1 ) C(k)=C(Multiflication,Addition)=(1,1) C(k)=C(Multiflication,Addition)=(1,1)
对于所有的k来说, C = ( N , N ) C=(N,N) C=(N,N)
那么接下来将 X e v e n [ k ] Xeven[k] Xeven[k]和 X o d d [ k ] Xodd[k] Xodd[k]再次分为奇数项和偶数项 X e e [ k ] Xee[k] Xee[k] X e o [ k ] Xeo[k] Xeo[k]和 X o e [ k ] Xoe[k] Xoe[k] X o o [ k ] Xoo[k] Xoo[k]
不断地向下分,直到不能分为止,我们就得到了下面的树状图:
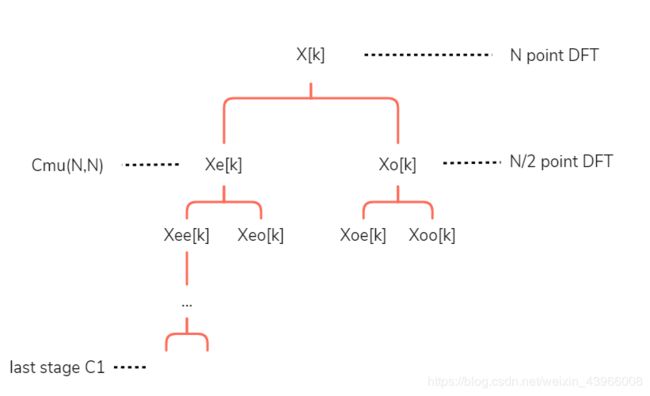
由于上述假设了 N = 2 μ N=2^{\mu } N=2μ,所以树状图共有 μ = log 2 N \mu=\log_2N μ=log2N级,我们定义最底层的算法复杂度为 C 1 C1 C1,则最顶端的算法复杂度为
C μ = ( N , N ) C\mu=(N,N) Cμ=(N,N)
则
C μ − 1 = 2 ( N 2 , N 2 ) = ( N , N ) 每 组 有 N 2 个 点 , 共 2 组 . . . . . . C μ − i = 2 i ( N 2 i , N 2 i ) = ( N , N ) 每 组 有 2 i 个 点 , 共 2 i 组 C\mu-1=2(\frac{N}2,\frac{N}2)=(N,N) 每组有\frac{N}2个点,共2组\\ ...\\ ...\\ C\mu-i=2^{i}(\frac{N}{2^{i}},\frac{N}{2^{i}})=(N,N)每组有{2^{i}}个点,共2^{i}组\\ Cμ−1=2(2N,2N)=(N,N)每组有2N个点,共2组......Cμ−i=2i(2iN,2iN)=(N,N)每组有2i个点,共2i组
所以每层向上一层的计算次数都是(N,N),求和得到总的蝶形运算次数:
C = ∑ i = 1 N C i = μ ( N , N ) = ( N log 2 N , N log 2 N ) = O ( N log 2 N ) C=\sum_{i=1}^{N}Ci=\mu(N,N)=(N\log_2N,N\log_2N)=O(N\log_2N) C=i=1∑NCi=μ(N,N)=(Nlog2N,Nlog2N)=O(Nlog2N)
而正常的傅里叶变换为 O ( N 2 ) O(N^2) O(N2)
举个例子说明这是多么大的飞跃:
假设计算机的单次计算速度为 T = 1 0 − 8 s e c T=10^{-8}sec T=10−8sec,共有 N = 2 20 N=2^{20} N=220个数据
T d f t = N 2 T = 1 0 4 s e c = 2.8 h T f f t = N log 2 N T = 0.2 s e c Tdft=N^2T=10^4sec=2.8h\\ Tfft=N\log_2NT=0.2sec Tdft=N2T=104sec=2.8hTfft=Nlog2NT=0.2sec
差了好多好多倍啊!!!
MATLAB代码
matlab有现成的fft2函数来做快速傅里叶变换。
%% Q3 2D-FFT
raw_image=imread('hh.jpg'); % read image
image=im2double(rgb2gray(raw_image));
tic % start counting
F=fft2(image); % 2D FFT
toc % stop counting
subplot(1,2,1),imshow(raw_image),title('raw');
subplot(1,2,2),imshow(F),title('2D-FFT');