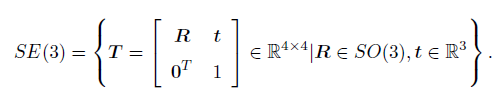《高翔SLAM十四讲》学习笔记ch1-ch3
路线总领
主线:《SLAM十四讲》书本+高翔的视频观看
辅助:《计算机视觉life》SLAM知识星球的资源,利用起来
书本的知识点分布
第一部分为数学基础篇,我们会以浅显易懂的方式,铺垫与视觉SLAM 相关的数学
知识,包括:
• 第一讲是前言,介绍这本书的基本信息,习题部分主要包括一些自测题。
• 第二讲为SLAM 系统概述,介绍一个SLAM 系统由哪些模块组成,各模块的具体工作是什么。实践部分介绍编程环境的搭建过程以及IDE 的使用。
• 第三讲介绍三维空间运动,你将接触旋转矩阵、四元数、欧拉角的相关知识,并且在Eigen 当中使用它们。
• 第四讲为李群和李代数。如果你现在不懂李代数为何物,也没有关系。你将学习李代数的定义和使用方式,然后通过Sophus 操作它们。
• 第五讲介绍针孔相机模型以及图像在计算机中的表达。你将用OpenCV 来调取相机的内外参数。
• 第六讲介绍非线性优化,包括状态估计理论基础、最小二乘问题、梯度下降方法。你会完成一个使用Ceres 和g2o 进行曲线拟合的实验。
这些就是我们所有的数学了,当然还有你以前学过的高等数学和线性代数。我保证它们看起来都不会很难——当然若你想进一步深入挖掘,我们会提供一些参考资料供你阅读,那些材料可能会比正文里讲的那些难一点。
第二部分为SLAM 技术篇。我们会使用第一部分所介绍的理论,讲述视觉SLAM中各个模块的工作原理。
• 第七讲为特征点法的视觉里程计。该讲内容比较多,包括特征点的提取与匹配、对极几何约束的计算、PnP 和ICP 等。在实践中,你将用这些方法去估计两个图像之间的运动。
• 第八讲为直接法的视觉里程计。你将学习光流和直接法的原理,然后利用g2o实现一个简单的RGB-D 直接法。
• 第九讲为视觉里程计的实践章,你将搭建一个视觉里程计框架,综合应用先前学过的知识,实现它的基本功能。从中你会碰到一些问题,例如优化的必要性、关键帧的选择等。
• 第十讲为后端优化,主要为Bundle Adjustment 的深入讨论,包括基本的BA以及如何利用稀疏性加速求解过程。你将用Ceres 和g2o 分别书写一个BA 程序。
• 第十一讲主要讲后端优化中的位姿图。位姿图是表达关键帧之间约束的一种更紧凑的形式。你将用g2o 和gtsam 对一个位姿球进行优化。
• 第十二讲为回环检测,我们主要介绍以词袋方法为主的回环检测。你将使用dbow3 书写字典训练程序和回环检测程序。
• 第十三讲为地图构建。我们会讨论如何使用单目进行稠密深度图的估计(以及这是多么不可靠),然后讨论RGB-D 的稠密地图构建过程。你会书写极线搜索与块匹配的程序,然后在RGB-D 中遇到点云地图和八叉树地图的构建问题。
• 第十四讲主要介绍当前的开源SLAM 项目以及未来的发展方向。相信阅读了前面的知识之后,你会更容易理解它们的原理,实现自己的新想法。最后,如果你完全看不懂上面在说什么,恭喜你!这本书很适合你!加油!
SLAM定义
SLAM是指当某种移动设备(如机器人、无人机、手机等)从一个未知环境里的未知地点出发,在运动过程中通过传感器(如激光雷达、摄像头等)观测定位自身位置、姿态、运动轨迹,再根据自身位置进行增量式的地图构建,从而达到同时定位和地图构建的目的。
SLAM框架
深度相机,又称RGB-D 相机
图像在计算机里只是一个数值矩阵。这个矩阵里表达着什么东西,计算机毫无概念(这也正是现在机器学习要解决的问题)。而视觉SLAM 中,我们只能看到一个个像素,知道它们是某些空间点在相机的成像平面上投影的结果。所以,为了定量地估计相机运动,必须在了解相机与空间点的几何关系之后进行。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传
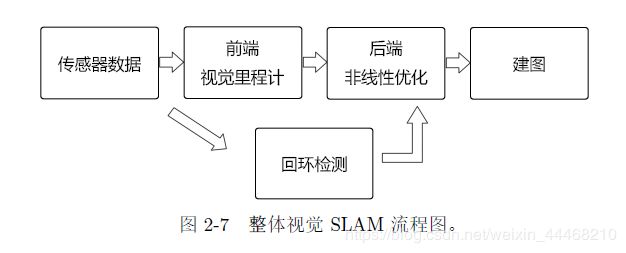
在视觉SLAM 中,前端和计算机视觉研究领域更为相关,比如图像的特征提取与匹配等,后端则主要是滤波与非线性优化算法
SLAM 问题的数学表述
运动方程和观测方程
首先,我们要说明机器人位置x 是什么。我们方才说位置是有些模糊的。也许读者能够理解在平面中运动的小萝卜,可以用两个坐标加一个转角的形式将位置参数化。然而,虽然我的漫画风格有些二次元,小萝卜更多时候是一个三维空间里的机器人。我们知道三维空间的运动由三个轴构成,所以小萝卜的运动要由三个轴上的平移,以及绕着三个轴的旋转来描述,这一共有六个自由度。那是否意味着我随便用一个R6 中的向量就能描述它了呢?我们将发现事情并没有那么简单。对六自由度的位姿¬,如何表达它,如何优化它,都需要一定篇幅来介绍,这将是第三讲和第四讲的主要内容。随后,我们要说明在视觉SLAM 中,观测方程如何参数化。换句话说,空间中的路标点是如何投影到一张照片上的。这需要解释相机的成像模型,我们将在第五章介绍。最后,当我们知道了这些信息,怎么求解上述方程?这需要非线性优化的知识,则是第六讲的内容。
LINUX下的cmake操作和库操作
头文件和库文件,见P34 ,需要再看cmake practice;
补充1:拷贝多个文件来到需要的位置
cp /home/usr/dir/{file1,file2,file3,file4} /home/usr/destination/
补充2:Clion的调用
cd clion-2016.2.2/bin/
./clion.sh
三维空间刚体运动
概念细核:旋转矩阵、旋转向量、四元数、欧拉角

机器人运动:世界坐标系和移动坐标系
旋转
旋转矩阵:自己的逆是自己的转置,同时它的行列式的值为1;旋转矩阵可以描述相机的旋转
理解旋转矩阵的下标:
平移
齐次坐标:将旋转和平移写在一个矩阵里;方式是给三维向量加一个维度
变换矩阵T ,它具有比较特别的结构:左上角为旋转矩阵,右侧为平移向量,左下角为0 向量,右下角为1。这种矩阵又称为特殊欧氏群
Eigen运算
没有自动类型提升,float类型的矩阵不能和int类型的矩阵相乘
Eigen特征值特征向量的计算是最重要的
旋转向量
这是更紧凑的描述旋转,因为旋转矩阵用了十六个量表达了六自由度的变换,不够紧凑;
任意旋转都可以用一个旋转轴和一个旋转角来刻画;
我们可以使用一个向量,其方向与旋转轴一致,而长度等于旋转角。这种向量,称为旋转向量(或轴角,Axis-
Angle)。这种表示法只需一个三维向量即可描述旋转。同样,对于变换矩阵,我们使用一个旋转向量和一个平移向量即可表达一次变换。这时的维数正好是六维。
欧拉角
常见的 rpy 角的旋转顺序是 ZYX
存在重大的问题是万向锁
四元数(听3BLUE的视频补课)
四元数可以优雅的描述并且计算三维旋转
代码中的四元数,初始化写的顺序是:W,X,Y,Z
如果题目中给的是X,Y,Z,W 需要转变一下
补充:OPENCV的编译使用
g++ -o main main.cpp `pkg-config opencv --cflags --libs` //main是可执行程序,main.cpp是代码,后面是编译选项