机器学习之集成学习(Ensemble Learning )③——AdaBoost

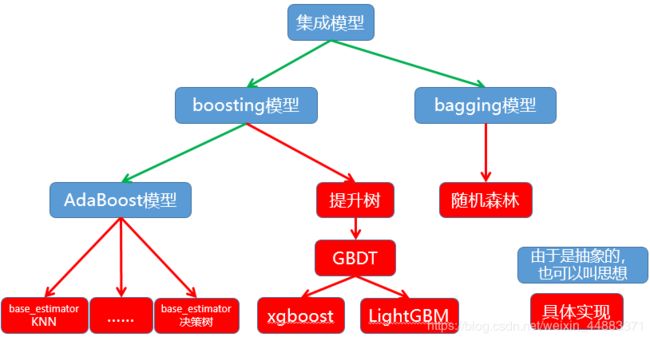
集成模型

Adaboost（1995）介绍及思想

该模块sklearn.ensemble包括由Freund和Schapire [FS1995]于1995年推出的流行的增强算法AdaBoost 。

AdaBoost的核心原则是在重复修改的数据版本上拟合一系列弱学习者（即，仅比随机猜测略好的模型，
例如小决策树）。然后通过加权多数投票（或总和）将来自所有这些预测的预测组合以产生最终预测。
每次所谓的增强迭代的数据修改包括应用权重， ，...，  每个训练样本。最初，这些权重都设置为 因
此，第一步只是训练一个弱学习者的原始数据。对于每次连续迭代，单独修改样本权重，并将学习算法
重新应用于重新加权数据。在给定步骤中，由前一步骤引起的增强模型错误预测的那些训练样本的权重
增加，而权重减少则正确预测的那些。随着迭代的进行，难以预测的示例会受到越来越大的影响。因
此，每个随后的弱学习者被迫集中于序列[HTF]中先前的错过的示例 。

定义

• Adaboost是一种迭代算法，其核心思想是针对同一个训练集训练不同的分类器(弱分类器)，然后把这些弱分类器集合起来，构成一个更强的最终分类器（强分类器）。
  介绍
• AdaBoost，是“Adaptive Boosting”（自适应增强）的缩写，是一种机器学习方法，由Yoav Freund和Robert Schapire于1995年提出。
  思想
• 前面的模型对训练集预测后，在每个样本上都会产生一个不同损失，AdaBoost会为每个样本更新权重，分类错误的样本要提高权重，分类正确的样本要降低权重，下一个学习器会更加“关注”权重大的样本；每一次得到一个模型后，根据模型在该轮数据上的表现给当前模型设置一个权重，表现好的权重大，最终带权叠加得到最终集成模型。

Adaboost思想的优缺点

优点：

• 可以使用各种回归分类模型来构建弱学习器，非常灵活
• Sklearn中对AdaBoost的实现是从带权学习视角出发的，思想朴素，易于理解
• 控制迭代次数可以一定程度防止发生过拟合

缺点：

• 对异常样本敏感，异常样本在迭代中可能会获得较高的权重，影响最终预测准确性。

Adaboost算法的基本思路

假设我们的训练集样本是

• T={(x,y1),(x2,y2),…(xm,ym)}

训练集的在第k个弱学习器的输出权重为

• $D(k)=(w_{k1},w_{k2},...w_{km});w_{1i}=\frac{1}{m};i=1,2...m$

首先我们看看Adaboost的分类问题。

分类问题的误差率很好理解和计算。由于多元分类是二元分类的推广，这里假设我们是二元分类问题，输出为{-1，1}，则第k个弱分类器$G_k(x)$在训练集上的加权误差率为

• $e_k=P(G_k(xi)$ ≠ $y_i)={\sum }_{i=1}^m{w}_{ki}I(G_k(x_i)$≠$y_i)$

---

接着我们看弱学习器权重系数,对于二元分类问题，第k个弱分类器$G_k(x)$的权重系数为

• ${\alpha }_k=\frac{1}{2}log\frac{1-e_k}{e_k}$

为什么这样计算弱学习器权重系数？从上式可以看出，如果分类误差率$e_k$越大，则对应的弱分类器权重系数${\alpha }_k$越小。也就是说，误差率小的弱分类器权重系数越大。

---

第三个问题，更新更新样本权重D。假设第k个弱分类器的样本集权重系数为D(k)=$(w_{k1},w_{k2},...w_{km})$，则对应的第k+1个弱分类器的样本集权重系数为

• $w_{k+1},i=\frac{w_{ki}}{Z_K}exp(-\alpha k{y}_i{G}_k(x_i))$

这里$Z_k$是规范化因子

• $Z_k={\sum }_{i=1}^{m}w{k}_{i}exp(-\alpha k{y}_i{G}_k(x_i))$

从$w_{k+1},i$计算公式可以看出，如果第i个样本分类错误，则$y_i{G}_k(xi)<0$，导致样本的权重在第k+1个弱分类器中增大，如果分类正确，则权重在第k+1个弱分类器中减少.

---

最后一个问题是集合策略。Adaboost分类采用的是加权表决法，最终的强分类器为

• $f(x)=sign({\sum }_{K=1}^K\alpha k{G}_k(x))$

---

小结

Adaboost底层代码实现(对应上述公式)

import pandas as pd
import numpy as np
from sklearn.tree import DecisionTreeClassifier
df = pd.DataFrame([[0,1],[1,1],[2,1],[3,-1],[4,-1],
                   [5,-1],[6,1],[7,1],[8,1],[9,-1]])

X = df.iloc[:,:-1]
Y = df.iloc[:,-1]

w = np.ones(len(df))/len(df)    #初始化权值分布
M = []                          #模型集合
A = []                          #学习器权重集合
n_trees = 3

for i in range(n_trees):
    model = DecisionTreeClassifier(max_depth=1)  ##训练第1个模型
    model.fit(X,Y,sample_weight=w)
    M.append(model)

    e = sum(w[model.predict(X)!=Y])         #误差率
    a =  0.5*np.log((1-e)/e)                #学习器系数
    A.append(a)

    z =  sum(w*np.exp(-a*Y*model.predict(X)))#规范因子
    #更新权值分布
    w = w/z*np.exp(-a*Y*model.predict(X)).values

res = 0
for i in range(n_trees):
    res += A[i] * M[i].predict(X)
np.sign(res)
print(res)

[ 0.32125172  0.32125172  0.32125172 -0.52604614 -0.52604614 -0.52604614
  0.97803126  0.97803126  0.97803126 -0.32125172]

---

Adaboost调库代码实现

一、

import pandas as pd
df = pd.DataFrame([[1,5.56],[2,5.7],[3,5.91],[4,6.4],[5,6.8],
                   [6,7.05],[7,8.9],[8,8.7111],[9,9.0],[10,9.05]])
X = df.iloc[:,[0]]
Y = df.iloc[:,-1]

from sklearn.ensemble import AdaBoostRegressor
from sklearn.tree import DecisionTreeRegressor

model = DecisionTreeRegressor(max_depth=3)
model = AdaBoostRegressor(n_estimators=5,base_estimator=model,learning_rate=0.01).fit(X,Y)
print(model.predict(X))

[5.56   5.7    5.91   6.4    6.8    7.05   7.05   8.7111 9.     9.05  ]

---

二、

import pandas as pd
df = pd.DataFrame([[0,1],[1,1],[2,1],[3,-1],[4,-1],
                   [5,-1],[6,1],[7,1],[8,1],[9,-1]])
X = df.iloc[:,[0]]
Y = df.iloc[:,-1]

from sklearn.ensemble import AdaBoostClassifier
model = AdaBoostClassifier(n_estimators=10,).fit(X,Y)
print(model.predict(X))

[ 1  1  1 -1 -1 -1  1  1  1 -1]

---

三、

import pandas as pd
df = pd.read_csv("../../datas/covtype.data",sep=",",header=None)
X = df.iloc[:,0:-1]
Y = df.iloc[:,-1]

from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size = 0.3)

from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier

myTree = DecisionTreeClassifier(max_depth=10)
model = AdaBoostClassifier(n_estimators=10,base_estimator=myTree)
model.fit(X_train,Y_train)

print(model.score(X_test,Y_test))
pd.crosstab(Y_test,model.predict(X_test),rownames=["label"],colnames=["predict"])

0.6839774187626216

---

Adaboost超参数

sklearn.ensemble.AdaBoostClassifier（base_estimator = None，n_estimators = 50，learning_rate = 1.0，algorithm =‘SAMME.R’，random_state = None ）
参数

• base_estimator ： object，optional（default = None）
  构建增强系综的基础估计器。需要支持样本加权，以及正确 classes_和n_classes_属性。如果None，则基本估算器是DecisionTreeClassifier(max_depth=1)
• n_estimators ： 整数，可选（default = 50）
  提升终止的最大估计数。在完美契合的情况下，学习过程提前停止。
• learning_rate ： float，optional（default = 1。）
  学习率会缩小每个分类器的贡献 learning_rate。在learning_rate和 之间需要权衡n_estimators。
• algorithm ： {‘SAMME’，‘SAMME.R’}，可选（default =‘SAMME.R’）
  如果’SAMME.R’则使用SAMME.R真正的增强算法。 base_estimator必须支持类概率的计算。如果’SAMME’则使用SAMME离散增强算法。SAMME.R算法通常比SAMME快收敛，通过较少的增强迭代实现较低的测试误差。
• random_state ： int，RandomState实例或None，可选（default =None）
  如果是int，则random_state是随机数生成器使用的种子; 如果是RandomState实例，则random_state是随机数生成器; 如果为None，则随机数生成器是由其使用的RandomState实例np.random。

属性

• estimators_ ： 分类器列表
  拟合子估算器的集合。
• classes_ ： shape数组= [n_classes]
  类标签。
• n_classes_ ： int
  班级数量。
• estimator_weights_ ： 浮点数组
  提升整体中每个估算器的权重。
• estimator_errors_ ： 浮点数组
  增强系综中每个估计器的分类误差。
• feature_importances_ ： shape数组= [n_features]
  返回要素重要性（越高，功能越重要）。

方法

• decision_function(self, X) -----------------------计算决策函数X。
• fit（self，X，y [，sample_weight]） ----------从训练集（X，y）构建增强分类器。
• get_params（self[，deep]） --------------------获取此估算工具的参数。
• predict（self，X） 预测X的类。
• predict_log_proba（self，X） ----------------预测X的类日志概率。
• predict_proba（self，X） -----------------------预测X的类概率。
• score（self，X，y [，sample_weight]） —返回给定测试数据和标签的平均精度。
• set_params（self，\ * \ * params） -------------设置此估算器的参数。
• staged_decision_function（self，X） -------计算X每次增强迭代的决策函数。
• staged_predict（self，X） ------------------------返回X的分阶段预测。
• staged_predict_proba（self，X） --------------预测X的类概率。
• staged_score（self，X，y [，sample_weight]） 返回X，y的分阶段分数。

---

参考文献：

• https://www.cnblogs.com/pinard/p/6133937.htmlutm_source=tuicool&utm_medium=referral
• https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.AdaBoostClassifier.html#sklearn.ensemble.AdaBoostClassifier

Adaboost面试

集成模型下有bagging和boosting思想，Adaboost是最初（1995年）的boosting思想下的模型。
最初是应用在二分类上，后面延伸到回归和多分类

• 第一步：为每个样本初始化权重，等权，总和为1
• 第二步：使用支持带权学习的学习器，带权训练模型，fit(X,Y,sample_weight=w)
• 第三步：计算当前轮模型的误差率，推导出学习器权重
• 第四步：更新样本权重，分对的样本降低权重，分错的样本提升权重。
• 第五步：重复2~4 步骤
• 第六步：预测其实就是带权投票

Gbdt、xgboost、lightGBM