数据结构(C语言版) 第 四 章 串、数组和广义表 知识梳理 + 作业习题详解
目录
- 一、串
- 二、KMP算法
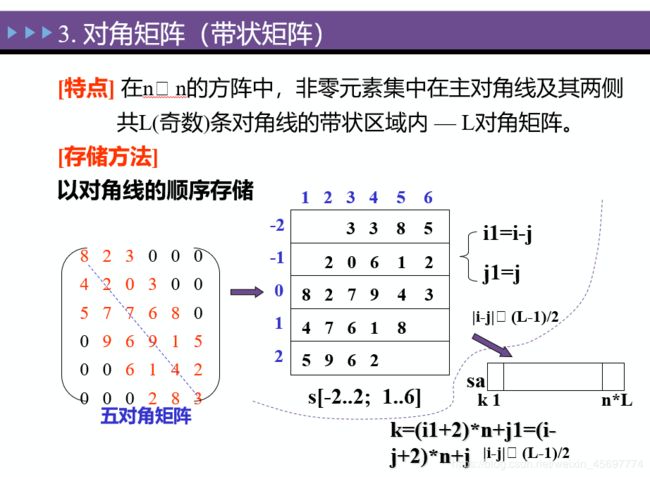
- 三、矩阵
- 四、广义表
- 五、作业习题
本系列博客为《数据结构》(C语言版)的学习笔记(上课笔记),仅用于学习交流和自我复习
数据结构合集链接: 《数据结构》C语言版(严蔚敏版) 全书知识梳理(超详细清晰易懂)
这一章实在没什么东西,我就放一些有点用的ppt和作业题吧(这一章的作业题写着是真的烦)
一、串
二、KMP算法
0x15.基本数据结构 — 字符串 (KMP算法(含详细证明)和最小表示法)
三、矩阵
四、广义表
五、作业习题
1.串是一种特殊的线性表,其特殊性体现在()
A.可以顺序存储
B.数组元素是一个字符
C.可以连续存储
D.数据元素可以是多个字符
答案:B
解析
串又称为字符串,是一种特殊的线性表,其特殊性体现在数据元素是一个字符,也就是说串是一种内容受限的线性表。(栈和队列是操作受限的线性表)
2.若串S=“software”,其子串的个数是( )。(2分)
A.8
B.37
C.36
D.9
答案:B
解析:
串中n个不同的字符,共有(n(n+1)) /2个真子串,空串也算的话再+1。
题中8个字符,(8x9)÷2=36,加上空串就是37。
3.假设以行序为主序存储二维数组A―array[1…100,1…100],设每个数据元素占2个存储单元,基地址为10,则LOC[5,5]=( )。
A.808
B.818
C.1010
D.1020
答案
B
解析
公式: L o c ( A i j ) = 10 ( 基 地 址 ) + [ ( 5 − 1 ) ∗ 100 + ( 5 − 1 ) ] ∗ 2 = 818 Loc(A_{ij})=10(基地址)+[(5-1)*100+(5-1)]*2=818 Loc(Aij)=10(基地址)+[(5−1)∗100+(5−1)]∗2=818。
4.数组A[0…4,-1…-3,5…7]中含有元素的个数()
A55
B45
C36
D16
答案:B
解析:三维数组:
长的边 个数:4-0+1=5
宽的 边 个数 :(-1)-(-3)+1=3
高的边个数 :7-5+1=3
总个数:533
5.设有一个10阶的对称矩阵A,采用压缩存储方式,以行序为主存储,a1,1为第一元素,其存储地址为1,每个元素占一个地址空间,则a8,5的地址是______。
A.13
B.33
C.18
D.40
答案
B
答案解析
这里数组下标从1开始,对称矩阵,只存储其下三角形元素,在a8,5的前面有7行,第1行有1个元素,第2行有2个元素,…,第7行有7个元素,这7行共有(1+7)×7/2=28个元素,在第8行中,a8,5的前面有4个元素,所以,a8,5前有28+4=32个元素,其地址为33。
6.数组A[0…5,0…6]的每个元素占5个字节,将其按列优先次序存储在起始地址为1000的内存单元中,则元素A[5,5]的地址是
答案:1175
这类题目分为两类:行优先和列优先(假设数组为A[n][m],数组下标从0开始)
1.行优先:基址+(行数)m+列数)×每个元素所占内存单位
2.列优先:基址+(列数n+行数)×每个元素所占内存单位,即1000+(5×6+5)×5=1175
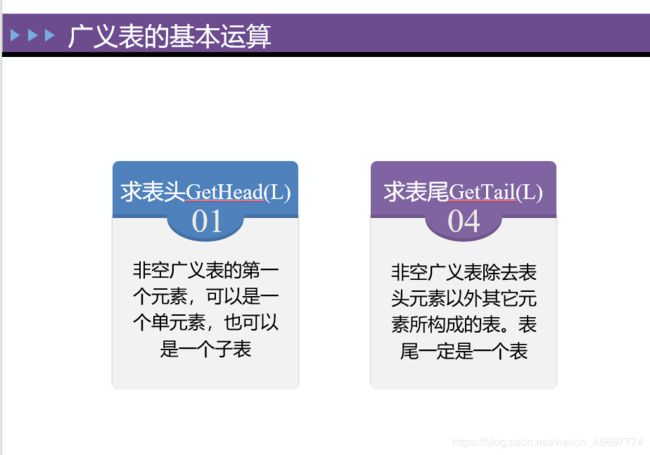
7.广义表((a,b,c,d))的表头和表尾分别是什么?
显然,广义表((a,b,c,d))中只有1个元素,
即(a,b,c,d)
表头是(a,b,c,d),一个子表
表尾是空表()长度为0
8.设广义表L= ((a, b,c)), 则L的长度和深度分别是()
A.1和1
B.1和3
C.1和2
D.2和3
答案:C
只有一个元素长度是1.唯一的元素里嵌套一层,所以深度是2
9.下面的说法不正确的是( )。
A.广义表的表头总是一个广义表
B.广义表的表尾总是一个广义表
C.广义表难以用顺序存储结构
D.广义表可以是一个多层次的结构
答案:A
10.已知广义表LS=((a,b,c),(d,e,f)),运用head和tail函数取出LS中原子e的运算是
tail操作是除掉头的所有,包含括号
LS= ((a,b,c),(d,f)故:
tail(LS)= ((d,e,f))
head(tail(LS))=(d,e,f)
tail(head(tail(Ls)))=(e,f)
head (tail(head(tail(ls))))=e
11.设有数组 A[i,j],数组的每个元素长度为 3 字节,i 的值为 1 到 8,j 的值为 1 到 10,数组从内存首地址 BA 开始顺序存放,当用以列为主存放时,元素 A[5,8] 的存储首地址为( )。(2分)
A.BA+141
B.BA+180
C.BA+222
D.BA+225
答案:B
这里是以列为主存放
本题A[5,8]以列为主,该元素处于第八列,前七列是满的每列8个元素,该元素处于第五行,他的前一个元素A[4,8]的结束地址就是所求的开始,最后,每个元素占3。所以有公式:(7*8+4)*3 = 180
12.若有 n 阶对称矩阵 A,以行序为主序方式,将其下三角形的元素(包括主对角线上所有元素)依次存放于一维数组B[1…(n(n+1))/2]中,则在 B 中确定 a[i, j](i
B.j*(j-1)/2+i
C.i*(i+1)/2+j
D.j*(j+1)/2+i
答案:B
n阶对称矩阵中的元素满足下述条件:aij=aji,(1<=i,j<=n)。对称矩阵中的每一对数据元素可以共用一个存储空间,因此可以将n2个元素压缩存储到n(n+1)/2个元的空间中,即可以一维数组保存。
假设用一维数组B[n(n+1)/2]作为对称矩阵A的存储结构,则B[k]和矩阵元素aij的下标i、j的对应关系为:
当i>-j时,k=i(i-1)/2+i;
当i<j时,k=j(j-1)/2+i;
(以上公式是针对aij和aji保存在同一个单元中的情况)
因为存储下三角元素,所以i<j,k=j(j-1)/2+i。
13.二维数组A的每个元素是由6个字符组成的串,其行下标i=0,1,…,8,列下标j=1,2,…,10。若A按行先存储,元素A[8,5]的起始地址与当A按列先存储时的元素( )的起始地址相同。设每个字符占一个字节。
A.A[8,5]
B.A[3,10]
C.A [5,8]
D.A[0,9]
正确答案
B
答案解析
二维数组A[0:8,1:10],设起始地址为0,数组元素A[i,j]按行存储公式为:Loc(A[i,j])=L1+(i-1)×U2×d+(j-1)×d,数组元素A[i,j]按列存储公式为:Loc(A[i,j])=L1+(j-1)×U2×d+(i-1)×d,可得i=3,j=10。
14.设二维数组 A [ 1.. m ] [ 1.. n ] A[1..m][1..n] A[1..m][1..n](即m行n列)按行存储在数组 B [ 1.. m ∗ n ] B[1..m*n] B[1..m∗n]中,则二维数组元素 A [ i ] [ j ] A[i][j] A[i][j]在一维数组B中的下标为()
A. ( i − 1 ) ∗ n + j (i-1)*n+j (i−1)∗n+j
B. ( i − 1 ) ∗ n + j − 1 (i-1)*n+j-1 (i−1)∗n+j−1
C . i ∗ ( j − 1 ) .i*(j-1) .i∗(j−1)
D. j ∗ m + i − 1 j*m+i-1 j∗m+i−1
A[ i, j ]在i 行前有 i - 1 行,就有(i - 1) * n 个元素,再加上它是在 j 列,所以就是 (i - 1) * n + j,注意这里数组下标是从1开始的,所以不需要减1