【LeetCode 004】各种分类讨论,已更新AC
【写不出来不肯睡觉系列。。。。。。】
成败 <=== 细节 <=== 清晰头脑 <=== 冷静
======================================================================================================
思想小总结:
昨晚睡觉前突然想着写道算法题,打开LeetCode选了个Hard的就开始了。
题目很清楚,给定两个有序数组,求出在两个有序数组结合起来后的中位数,其实就是求在整体中第K小数,要求时间复杂度是log级别。
题目的本质就成了找第K小数。
log级的算法,那么思路很清楚,就是分治法,且原数组已经有序,那么基本肯定就是二分法了。
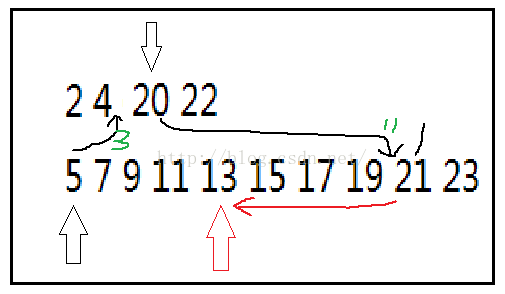
已经有序了,那就是定需要查找的值key,很自然想到了拿一个数组的第一个值去另一个数组搜索。
搜索后,可以确定,两个数组综合后的,前cur个的整体顺序,拿很自然在拿另一个数组的下一个元素在之前那个数组搜索,一直迭代即可。
看图后思路变很清楚。
实质就是第k小数
其实就是找在num1数组 + num2数组中的,第k = (len1 + len2) / 2小的数
很快写好了,结果懵逼了。因为长度奇数,偶数,下标-1,有可能跳到另一个数组,等等分类讨论情况。
结果,因为没有仔细想清楚,想到什么情况就分什么情况了,结果越分越多,越分越乱,结果就是写了狗屎一样的代码,一般写到这种情况,基本95%都是错的了,由于比较困了,思路也变得不是很清晰,但是写不出来又觉得很不爽,
接着就想啊改啊,测啊,改啊,调啊,试啊,。。。。恶性傻逼循环。。。。一般不可能在这种情况下解决问题的。
就有了。。。。。。。。。。。。。。。。。。。。。。。。。。简直让我在凌晨,舍友们都已经关灯睡觉了,抓狂啊,这一大排的Wrong Answer,我内心是崩溃的
就这样苦苦挣扎到了凌晨三点,真是不应该。。。。。。
誓不罢休的精神倒是一直没变,虽然是件好事,不过应该注意一下身体比较好。
直到今天有时间了,好好重新分析了一下,仔细分类讨论一下,冷静。
思路一下变得很清晰,很快重新实现了,而且代码明显短了,明显漂亮了。的确,一般正确的代码都应该是比较短,比较漂亮的。
写完,提交,一次AC,哈哈,简直太开心了!
不管写算法,还是做事情,冷静的分析,清晰的逻辑真的很重要。
即使你再想,再着急,如果不能好好冷静下来,那基本上就是前面提到的傻逼恶性循环,然后得到一大排惨不忍睹的WA。
还是让自己冷静下来,思路变得清晰的时候,才有可能漂亮的解决问题。
这样的经历其实每个人都有,而且是经常有,经常因为太想着结果,而变得着急,不冷静,就方了,这种时候往往结果都比较糟糕。
作为一个小总结,希望以后可以有更好的意识。
end of 思想总结
======================================================================================================
问题链接:
https://leetcode.com/problems/median-of-two-sorted-arrays/
问题描述:
给定有序数组nums1, nums2, 找出在num1和nums2综合后的中位数,要求时间复杂度log级别
问题本质,相当于找出num1+nums2的第k小数。
解题思路:
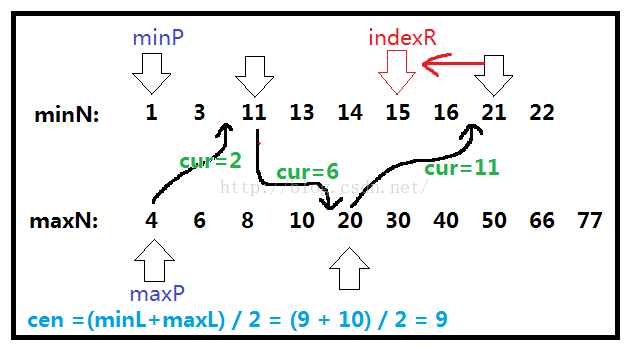
核心思路如图:
图1. cur >= cen后回退,目标indexR = minP - (cur - cen)
1. cur < cen 的时候一直重复交叉二分搜素
2. 两种情况停止搜索,minN用光了,cur >= cen
3. 停止搜索后可以分3种情况
1) minN用光了,又分两种情况
1> cur < cen, 还没找到,所以得往没用光的maxN后面继续扩展
2> cur >= cen,意味着已经找到,往前回退cur - cen 格即可
2) 最后一次在minN二分搜索,且此时满足,cur >= cen,意味着已经找到,往前回退cur - cen 格即可
3) 最后一次在maxN二分搜索,且此时满足,cur >= cen,意味着已经找到,往前回退cur - cen 格即可
通过分析,可以把上面4个情况合并成两个情况:
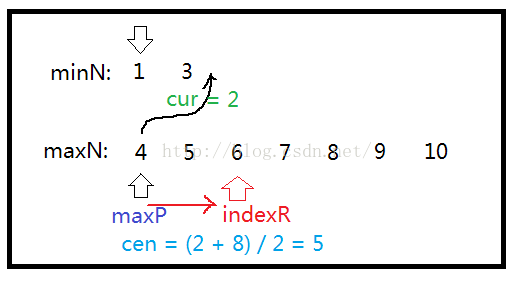
1) 第一种情况:(图2情况)
minN用光了,且 cur < cen, 还没找到,所以得往没用光的maxN后面继续扩展
2) 如果最后一次在maxN里二分搜索,则将minN和maxN两个数组的所有数据交换一下,则变成最后一次在minN二分搜素了,所以
第二种情况:(图1情况)
最后一次在minN二分搜索,且此时满足,cur >= cen,意味着已经找到,往前回退cur - cen 格即可
图2. minN用光且cur
总结:
1.
小心分类讨论,数组总长度,奇偶情况
2.
二分搜索里,注意lower和upper的区别
1, 1, 1, 2, 2, 2, 3, 3, 3 查找2
lower:
a[mid - 1] < key <= a[mid]
返回的是第一个2的下标
upper:
a[mid - 1] <= key < a[mid]
返回的是最后一个2的下标 + 1
此处,找到是目前《=key的所有值,故应该用upper
实现:
(头脑混乱时写的代码:),
分类讨论的时候简直是又臭又长,这种情况基本不可能写对
#include
#include
#include
using namespace std;
class Solution {
public:
int upper(vector a, int l, int r, int key){
if(a.size() == 0) return -1;
if (key <= a[l]) {
while(key == a[l]) l++;
return l;
}
int mid;
while (l <= r) {
mid = (l + r) >> 1;
if (a[mid - 1] <= key && key <=a[mid]) return mid;
if (a[mid - 1] >= key) {
r = mid - 1;
} else {
l = mid + 1;
}
}
return r + 1;
}
double findMedianSortedArrays(vector& nums1, vector& nums2) {
int minL = nums1.size();
int maxL = nums2.size();
vector minN;
vector maxN;
if (minL <= maxL) {
minN = nums1;
maxN = nums2;
} else {
minL = nums2.size();
maxL = nums1.size();
minN = nums2;
maxN = nums1;
}
int oneDone = -1;
if (minL == 0) {
oneDone = 0;
} else if(maxL == 0){
oneDone = 1;
}
int curL = 0;
int cen = (minL + maxL) / 2;
//printf("%d\n", cen);
int minP = 0;
int maxP = 0;
int index;
int minMax = 0;
while (curL < cen) {
if(oneDone != -1) break;
if(maxP + 1 < maxL && maxN[maxP] == maxN[maxP + 1]) {
maxP++;
curL++;
}
index = upper(minN, minP, minL - 1, maxN[maxP]);
// while(index < minL && maxN[maxP] == minN[index]) index++;
curL += index - minP;
minP = index;
minMax = 0;
//printf("cen = %d, curL = %d, minP = %d, maxP = %d, index = %d\n", cen, curL, minP, maxP, index);
if (minP >= minL){
oneDone = 0;
break;
}
if (curL >= cen) break;
if(minP + 1 < minL && minN[minP] == minN[minP + 1]) {
minP++;
curL++;
}
index = upper(maxN, maxP, maxL - 1, minN[minP]);
//while(index < maxL && minN[minP] == maxN[index]) index++;
curL += index - maxP;
maxP = index;
minMax = 1;
//printf("cen = %d, curL = %d, minP = %d, maxP = %d, index = %d\n", cen, curL, minP, maxP, index);
if (maxP >= maxL){
oneDone = 1;
break;
}
if (curL >= cen) break;
//int haha;
//scanf("%d",&haha);
}
double ans = 0;
if (oneDone == 0) {
if (curL > cen) {
int indexR = index - (curL - cen);
if ((minL + maxL) % 2 == 1) {
ans = minN[indexR];
} else {
int indexL = indexR - 1;
double cenR = minN[indexR];
double cenL = minN[indexL];
if (maxN[maxP] > minN[indexL]) {
cenL = maxN[maxP];
}
ans = (cenR + cenL) / 2.0;
}
} else {
int indexR = maxP + cen - curL;
if ((minL + maxL) % 2 == 1) {
ans = maxN[indexR];
} else {
int indexL = indexR - 1;
if (indexL >= 0) {
ans = (maxN[indexL] + maxN[indexR]) / 2.0;
}
if (minN[minL - 1] > maxN[indexL]) {
ans = (minN[minL - 1] + maxN[indexR]) / 2.0;
}
}
}
} else if (oneDone == 1) {
if (curL > cen) {
int indexR = index - (curL - cen);
if ((minL + maxL) % 2 == 1) {
ans = maxN[indexR];
} else {
int indexL = indexR - 1;
double cenR = maxN[indexR];
double cenL = maxN[indexL];
if (minN[minP] > maxN[indexL]) {
cenL = minN[minP];
}
//printf("%f %f\n", cenR, cenL);
ans = (cenR + cenL) / 2.0;
}
} else {
int indexR = minP + cen - curL;
if ((minL + maxL) % 2 == 1) {
ans = minN[indexR];
} else {
int indexL = indexR - 1;
if (indexL >= 0) {
ans = (minN[indexL] + minN[indexR]) / 2.0;
}
if(maxN[maxL - 1] > minN[indexL]){
ans = (maxN[indexL] + minN[indexR]) / 2.0;
}
}
}
} else {
if (curL == cen) {
if (minMax == 0) {//
if ((minL + maxL) % 2 == 1) {
ans = maxN[maxP];
} else {
double cenR = maxN[maxP];
double cenL = minN[index - 1];
if(maxP >= 0 && maxN[maxP - 1] > cenL) {
cenL = maxN[maxP - 1];
}
ans = (cenR + cenL) / 2.0;
}
} else {//
if ((minL + maxL) % 2 == 1) {
ans = minN[minP];
} else {
double cenR = minN[minP];
double cenL = maxN[index - 1];
if(minP >= 0 && minN[minP - 1] > cenL) {
cenL = minN[minP - 1];
}
ans = (cenR + cenL) / 2.0;
}
}
} else {
int indexR = index - (curL - cen);
if (minMax == 0) {
if ((minL + maxL) % 2 == 1) {
ans = minN[indexR];
} else {
double cenR = minN[indexR];
double cenL = minN[indexR - 1];
if (maxN[maxP] > minN[indexR - 1]) {
cenL = maxN[maxP];
}
ans = (cenR + cenL) / 2.0;
}
} else {
if ((minL + maxL) % 2 == 1) {
ans = maxN[indexR];
} else {
double cenR = maxN[indexR];
double cenL = maxN[indexR - 1];
if (minN[minP] > maxN[indexR - 1]) {
cenL = maxN[maxP];
}
ans = (cenR + cenL) / 2.0;
}
}
}
}
return ans;
}
};
int main() {
vector num1;
num1.push_back(2);
//num1.push_back(2);
// num1.push_back(3);
vector num2;
num2.push_back(1);
num2.push_back(3);
num2.push_back(4);
// num2.push_back(10);
// num2.push_back(11);
// num2.push_back(13);
// num2.push_back(15);
// num2.push_back(21);
// num2.push_back(22);
// num2.push_back(23);
// num2.push_back(24);
// num2.push_back(25);
// num2.push_back(26);
//
Solution s;
double ans = s.findMedianSortedArrays(num1, num2);
cout << ans << endl;
//cout << s.upper(num1, 0, 3, 4) << endl;
return 0;
} AC代码:
#include
#include
#include
using namespace std;
class Solution {
public:
int upper(vector a, int l, int r, int key){ // <= key <, 例如1,1,1,2里找1,返回2的下标3
if(a.size() == 0) return 0;
int mid;
while (l <= r) {
mid = (l + r) >> 1;
if (a[mid - 1] <= key && key < a[mid]) return mid;
if (a[mid - 1] > key) {
r = mid - 1;
} else {
l = mid + 1;
}
}
return l;
}
double findMedianSortedArrays(vector& nums1, vector& nums2) {
int minL = nums1.size();
int maxL = nums2.size();
vector minN; // 存储最大元素较小的数组
vector maxN; // 存储最大元素较大的数组
if (minL == 0 || ((maxL != 0) && nums1[minL - 1] <= nums2[maxL - 1])) {
minN = nums1;
maxN = nums2;
} else {
minN = nums2;
maxN = nums1;
}
minL = minN.size();
maxL = maxN.size();
int minNDone = minL == 0 ? 1 : 0;
int isOdd = (minL + maxL) % 2 == 1 ? 1 : 0;
int cur = 0; // 已确定第cur小数字,从0开始
int cen = (minL + maxL) / 2; // 目标下标 = 当(minL+maxL)%2,==1时cen一个点,==0时,cen和cen-1两个点之和/2
int minP = 0; // 数组的当前‘头’
int maxP = 0;
int index = 0;
int minMax; // = 0,表示在minN刚刚二分搜索。= 1表示刚刚在maxN二分搜索
while (cur < cen) {
if(minNDone == 1) break;
// maxN的'头'在minN里二分搜索 ======================================================
index = upper(minN, minP, minL - 1, maxN[maxP]);
cur += index - minP;
minP = index;
minMax = 0;
//printf("cen = %d, cur = %d, minP = %d, maxP = %d, index = %d\n", cen, cur, minP, maxP, index);
if (minP >= minL){
minNDone = 1;
break;
}
if (cur >= cen) break;
//minN的'头'在maxN里二分搜索 ======================================================
index = upper(maxN, maxP, maxL - 1, minN[minP]);
cur += index - maxP;
maxP = index;
minMax = 1;
//printf("cen = %d, cur = %d, minP = %d, maxP = %d, index = %d\n", cen, cur, minP, maxP, index);
if (cur >= cen) break;
}
double ans = 0;
int indexR;
// 小的数组用完了,且已经确定大小的下标 < 目标下标, 在maxN往后找,目标indexR = maxP + cen - cur;
if (cur < cen) {
indexR = maxP + cen - cur;
if (isOdd == 1) {
ans = maxN[indexR];
} else {
ans = (maxN[indexR] + maxN[indexR - 1]) / 2.0;
}
return ans;
}
// 最后一次二分搜索在maxN里结束,则minN和maxN交换身份,统一为最后一次在minN里二分搜索结束
if (minMax == 1) {
vector tmp = maxN;
maxN = minN;
minN = tmp;
int tmpP = maxP;
maxP = minP;
minP = tmpP;
}
if (cur == cen) {
// 正好命中
if (isOdd == 1) {
ans = maxN[maxP];
} else {
ans = (maxN[maxP] + minN[minP - 1]) / 2.0;
}
} else {
// 在这次二分搜索的那小段里,已经超过,所以要在minN回退,目标indexR = minP - (cur - cen);
indexR = minP - (cur - cen);
if (isOdd == 1) {
ans = minN[indexR];
} else {
ans = (minN[indexR] + minN[indexR - 1]) / 2.0;
}
}
return ans;
}
};
int main() {
vector num1;
num1.push_back(1);
num1.push_back(2);
vector num2;
num2.push_back(1);
num2.push_back(2);
Solution s;
double ans = s.findMedianSortedArrays(num1, num2);
cout << ans << endl;
return 0;
}