Kmeans、Kmeans++、Birch和KNN四种聚类算法对二维坐标点的聚类分析对比实验

0 写在前面（数据集和源代码）

本文章涉及到的数据集合所有代码均上传在此处：https://download.csdn.net/download/zhouzhuo_csuft/10494273；点击此处直接打开链接；一共有四个代码文件，分别是Kmeans、Kmeans++、Birch和KNN算法，四个算法对同一个数据集聚类分析进行对比试验。（本代码是本人自己书写，全部可用！）

1 引言

近年来，机器学习已成为计算机前沿中火热的研究点之一。我国政府也将机器学习纳入了国家级战略。目前，机器学习已广泛用于各种数据挖掘、模式识别、语音识别及图像处理等各领域。本文以机器学习中四个经典的聚类算法进行对比介绍和对比实验，得出四个算法对相同实验数据集的聚类效果。

2聚类算法

聚类在学术界并没有一个确切的定义，此处给出1974年Everitt对聚类的定义：一个类簇内的实体是相似的,不同类簇的实体是不相似的;一个类簇是测试空间中点的会聚,同一类簇的任意两个点间的距离小于不同类簇的任意两个点间的距离^[1];类簇可以描述为一个包含密度相对较高的点集的多维空间中的连通区域,它们借助包含密度相对较低的点集的区域与其他区域(类簇)相分离。

简单地说，聚类是根据其自身特征将数据集进行划分成若干类的过程，划分的结果是相同类哈哈内数据相似度尽可能大、不同类间数据相似度尽可能小，从而发现数据集的内在结构。

聚类在不同应用领域有不同的特殊要求，聚类算法的典型性能要求有以下几个方面：

（1）伸缩性

（2）兼容性

（3）有效处理噪声数据

（4）能处理基于约束的聚类

（5）可解释性和可用性

典型的聚类过程主要包括数据（样本）准备、特征选择和特征提取、相似度计算、聚类、对聚类结果进行有效性评估^[1]。

聚类过程：

（1）数据准备：包括特征标准化和降维。

（2）特征选择，从最初的特征中选取最有效的特征，并将其存储于向量中。

（3）特征提取：通过对所选择的特征进行转换形成新的突出特征。

（4）聚类：首先选择合适特征类型的某种离函数 ( 或构造新的距离函数 ) 进行接近程度的度量，而后执行聚类或分组。 .

（5）聚类结果评估 : 是指对聚类结果进行评估 . 评估主要有 3 种 : 外部有效性评估、内部有效性评估和相关性测试评估。

3 典型聚类及其变种算法介绍

3.1 K-Means聚类

3.2.1 K-Means聚类介绍

1967 年 ,MacQueen 首次提出了 K 均值聚类算法 (K-Means 算法 )。 迄今为止 , 很多聚类任务都选择该经典算法^[2]。该算法的核心思想是找出 k个聚类中心c₁ ,c₂ ,…,c_k使得每一个数据点 x_i 和与其最近的聚类中心 c_v 的平方距离和被最小化 ( 该平方距离和被称为偏差 D)。

3.1.2 K-means聚类算法步骤

（1）初始化，随机指定 K 个聚类中心 (c₁ ,c₂ ,…,c_k );

（2）分配 x_i, 对每一个样本 x_i，找到离它最近的聚类中心 c_v，并将其分配到 c_v 所标明类;

（3）修正 c _w，将每一个 c_w 移动到其标明的类的中心；

（4）计算偏差 ；

（5）判断D是否收敛，如果D收敛，则return(c₁,c₂,……,c_k)，并终止本算法；否则返回步骤2。

3.1.3 K-means 算法的优点与不足

优点: 能对大型数据集进行高效分类, 其计算复杂性为 O(tkmn), 其中 ,t 为迭代次数，k为聚类数，m 为特征属性数，n 为待分类的对象数，通常k,m,t<[3]. 在对大型数据集聚类时，K-means 算法比层次聚类算法快得多。

不足: 通常会在获得一个局部最优值时终止；仅适合对数值型数据聚类；只适用于聚类。

3.2 K-Means++算法

3.2.1 K-Means++简介

由于 K-means 算法的分类结果会受到初始点的选取而有所区别，因此后来有人针对这个问题对K-Means算法进行改进，于是产生了 K-means++算法 。K-Means++算法只是对初始点的选择有改进而已，其他步骤都一样。初始质心选取的基本思路就是，初始的聚类中心之间的相互距离要尽可能的远。

3.2.2  K-Means++算法步骤^[4]

（1）从数据集中随机选取一个样本作为初始聚类中心c1;

（2）首先计算每个样本与当前已有聚类中心之间的最短距离（即最近的一个聚类中心的距离），用D(x)表示；接着计算每个样本被选为下一个聚类中心的概率  。按照轮盘法选出下一个聚类中心;

（3）重复第2步，直到选择出共K个聚类中心；

（4）后面与K-Means聚类算法的2-4步相同。

3.3 BIRCH聚类算法

3.3.1 BIRCH聚类简介

　BIRCH的全称是利用层次方法的平衡迭代规约和聚类（Balanced Iterative Reducing and Clustering UsingHierarchies），它利用了一个类似于B+树的聚类特征树(ClusteringFeature Tree，简称CF Tree)快速的聚类。如图1所示，这颗树的每一个节点是由若干个聚类特征(Clustering Feature，简称CF)组成。每个节点包括叶子节点都有若干个CF，而内部节点的CF有指向孩子节点的指针，所有的叶子节点用一个双向链表链接起来。

不同于K-Means算法，BIRCH算法可以不用输入类别数K值。如果不输入K值，则最后的CF元组的组数即为最终的K，否则会按照输入的K值对CF元组按距离大小进行合并。一般来说，BIRCH算法适用于样本量较大的情况，除了聚类还可以额外做一些异常点检测和数据初步按类别规约的预处理。

 

图 1 CF Tree模型

3.3.2 BIRCH聚类算法步骤^[5]

（1）扫描所有数据，建立初始化的CF树，把稠密数据分成簇，稀疏数据作为孤立点对待；

（2）这个阶段是可选的，阶段（3）的全局或半全局聚类算法有着输入范围的要求，以达到速度与质量的要求，所以此阶段在阶段步骤（1）的基础上，建立一个更小的CF树；

（3）补救由于输入顺序和页面大小带来的分裂，使用全局/半全局算法对全部叶节点进行聚类

（4）这个阶段也是可选的，把阶段（3）的中心点作为种子，将数据点重新分配到最近的种子上，保证重复数据分到同一个簇中，同时添加簇标签。

3.3.4 BIRCH聚类的优缺点

主要优点有：

（1）节约内存，所有的样本都在磁盘上，CF Tree仅仅存了CF节点和对应的指针。

（2）聚类速度快，只需要一遍扫描训练集就可以建立CF Tree，CF Tree的增删改都很快。

（3）可以识别噪音点，还可以对数据集进行初步分类的预处理

主要缺点有：

（1）由于CF Tree对每个节点的CF个数有限制，导致聚类的结果可能和真实的类别分布不同.

（2）对高维特征的数据聚类效果不好。此时可以选择Mini Batch K-Means

（3）如果数据集的分布簇不是类似于超球体，或者说不是凸的，则聚类效果不好。

3.4 KNN聚类算法

3.4.1 KNN聚类简介

KNN（K-Nearest Neighbor），代表 k 个最近邻分类法，通过k个与之最相近的历史记录的组合来辨别新的记录。KNN 是一个众所周知的统计方法，在过去的 40 年里在模式识别中集中地被研究。KNN 在早期的研究策略中已被应用于文本分类^[6]，是基准 Reuters 主体的高操作性的方法之一。其它方法，如 LLSF、决策树和神经网络等。

3.4.2 KNN聚类算法步骤^[7]

（1）准备数据，对数据进行预处理；

（2） 选用合适的数据结构存储训练数据和测试元组；

（3）设定参数，如元组数目k；

（4）维护一个大小为k的按距离由大到小的优先级队列，用于存储最近邻训练元组。随机从训练元组中选取k个元组作为初始的最近邻元组，分别计算测试元组到这k个元组的距离，将训练元组标号和距离存入优先级队列；

（5）遍历训练元组集，计算当前训练元组与测试元组的距离，将所得距离L 与优先级队列中的最大距离Lmax；

（6）进行比较。若L>=Lmax，则舍弃该元组，遍历下一个元组。若L < Lmax，删除优先级队列中最大距离的元组，将当前训练元组存入优先级队列；

（7）遍历完毕，计算优先级队列中k 个元组的多数类，并将其作为测试元组的类别；

（8） 测试元组集测试完毕后计算误差率，继续设定不同的k值重新进行训练，最后取误差率最小的k 值。

3.4.3KNN聚类的优缺点

主要优点有

（1）简单，易于理解，无需建模与训练，易于实现；

（2）适合对稀有事件进行分类；

（3）适合与多分类问题，例如根据基因特征来判断其功能分类，KNN比SVM的表现要好。

主要缺点有：

（1）惰性算法，内存开销大，对测试样本分类时计算量大，性能较低；

（2）可解释性差，无法给出决策树那样的规则。

4 实验

4.1 实验环境

本实验拟将对第二节中的4个算法进行测试，实验系统采用Ubuntu16.04TLS版本（也可以用windows下pycharm等IDE），内存8G，CPU为4核心AMD芯片（两个），主频2.4GHZ。实验代码使用Python2.7.2版本。

4.2实验测试

      为测试4个算法的聚类效果，实验将使用4个算法对同一个数据集进行聚类测试。该数据集是一个存放80个二维坐标点的文本文件，文件每行有两个数据，以制表符分割，分别表示二维坐标的X轴数据和Y轴数据。

      经测试，4个算法对数据集聚类的结果图示如图2、图3、图4、图5所示：

                                      

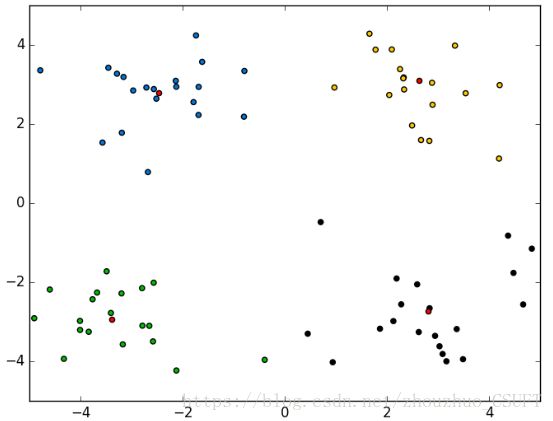
                                                                      图 2 K-Means聚类结果

                                 

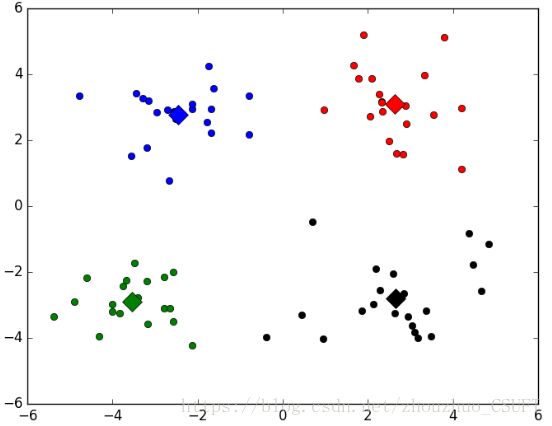
图 3 K-Means++聚类结果

                                            

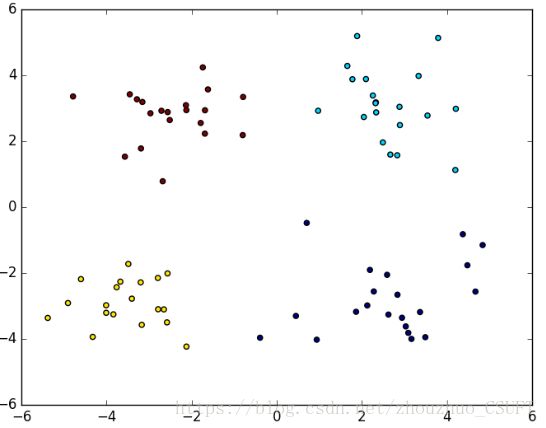
图 4 BIRCH聚类结果

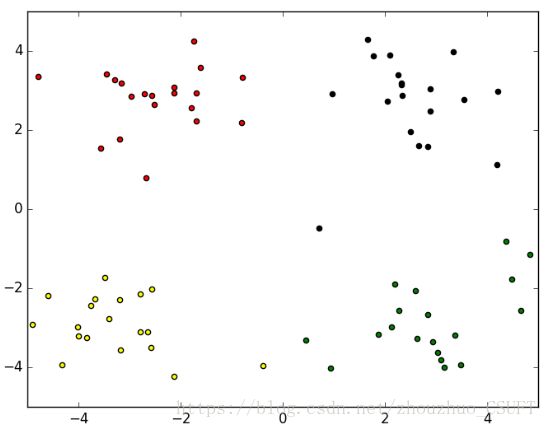
图 5 KNN聚类结果

4.3 对比结论

上述四组图为实验对比，可以看出，四种算法对数据集的分类效果相当，只有在个别点的划分有所不同，即数据集中的(-0.392370  -3.963704)坐标点，在K-Means聚类和KNN聚类中，该点被聚类到左下方簇中，而在K-Means++聚类和BIRCH聚类中，该点被划分到了右下方簇中。

5总结

      本文首先介绍了聚类算法定义和聚类算法的基本步骤，然后分别对K-Means、K-Means++、BIRCH和KNN四个经典的聚类算法作了详细介绍，最后通过对同一个数据集进行对比实验，得出四个聚类效果。从实验中反映了四个聚类算法对数据集的聚类效果较好。四种聚类算法在本实验中达到了的聚类效果几乎一样，但四类聚类算法在实际生活中仍将有其不同的使用背景，故在实际生活中需要结合特定的实际环境采用不同聚类算法，以达到最好的效果^[8]。

6参考文献

[1] 孙吉贵，刘杰，赵连宇.聚类算法研究[J].软件学报,2008

[2] 张建萍,刘希玉.基于聚类分析的 K-means算法研究及应用[J].计算机应用研究,2007,5

[3] 杨善林,李永森,胡笑旋,潘若愚.K-means 算法中的 k 值优化问题研究[J].系统工程理论与实践，2006,2

[4] David Arthur and Sergei Vassilvitskii.k-means++:[J].TheAdvantages of Careful Seeding，2007

[5] BIRCH:An Efficient Data 3Clustering Method forVery Large Databases[J].1996

[6]张宁,贾自艳,史忠植.使用 KNN算法的文本分类[J].计算机工程，2005.4

[7]KNN算法综述,https://wenku.baidu.com/view/d84cf670a5e9856a561260ce.html,2018.5.10

 [8]贺玲,吴玲达,蔡益朝.数据挖掘中的聚类算法综述[J].计算机应用研究,2007