简单易懂的人工智能系列：KNN算法（K近邻）

KNN算法原理

KNN概念

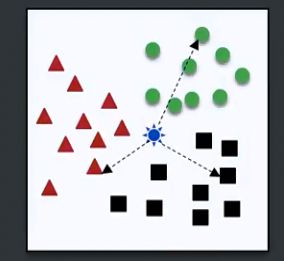
KNN：K-Nearest Neighbour，分类算法中最简单的算法之一，其核心思想是如果离某一个样本最近的k个样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性。KNN不但可以预测分类，含可以做回归分析（预测具体的值）。

有已知N个分类结果的样本点，对新纪录 r 使用KNN将其分类的步骤：

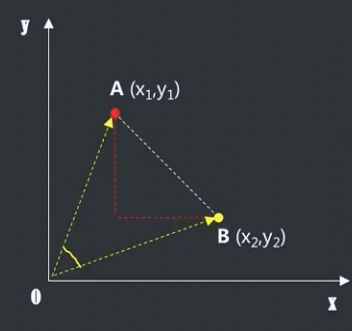
• step1：确定 k 值，确定计算距离的公式，比如欧式距离
• step2：计算 r 和其他样本点之间的距离 dir,其中i属于（1，N）
• step3：得到目前和 r 最接近的 k 个样本，作为 KNN 距离的样本
• step4：将k 个样本中最多归属类别的分类标签赋予新纪录 r，分类结束

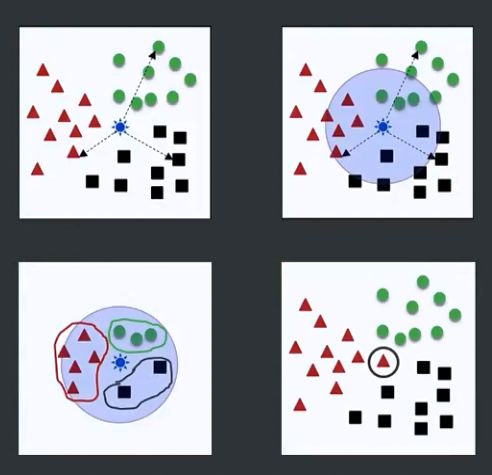
实施步骤图示

第一步，确定 K 值，确定距离公式

常见距离计算公式：

对于K 的取值不宜过大，一般使用交叉验证确定，本例中选择k = 10，距离公式选择欧氏距离（两点距离）。

第二步，计算r 和 所有样本点的距离

第三步，圈定符合条件的k个记录

将距离按升序排序，得到TOP k 小的值，选入KNN 样本。

第四步，统计样本分类，确定新记录 r 的分类

实现伪码

repeat

      计算已知类别数据集中的点与当前点之间的距离

      按照距离递增次序排序

until 样本点遍历完成

返回前k个样本点

统计k个样本点出现频率最高的类别标签

KNN算法优缺点

优点：

• 原理简单，容易理解，容易实现
• 重新训练代价较低
• 时间、空间复杂度取决于训练集（一般不算太大）

缺点

• KNN属于 lazy-learning 算法，得到 结果的及时性差
• k 值对结果影响大（试想一下，k = 1 和k =N 的极端情况）
• 不同累记录相差较大时容易误判
• 样本点较多时，计算量较大
• 相对于决策树，结果可解释性不强

kNN实战之约会网站配对效果判定

通过对KNN算法的详解，我们已经明白了算法的核心实现，但是这并不是完整的KNN算法进行分类的流程，KNN算法的一般流程：

 

• 收集数据：可以使用爬虫进行数据的收集，也可以使用第三方提供的免费或收费的数据。一般来讲，数据放在文件中，按照一定的格式进行存储，便于解析及处理
• 准备数据：使用Python解析、预处理数据
• 分析数据：可以使用很多方法对数据进行分析，例如使用Matplotlib将数据可视化
• 测试算法：计算错误率
• 使用算法：错误率在可接受范围内，就可以运行KNN进行分类

实战数据背景

海伦女士一直使用在线约会网站寻找适合自己的约会对象。尽管约会网站会推荐不同的任选，但她并不是喜欢每一个人。经过一番总结，她发现自己交往过的人可以进行如下分类：

• 不喜欢的人
• 魅力一般的人
• 极具魅力的人

约会数据存放在文本文件datingTestSet.txt中，每个样本数据占据一行，总共有1000行。

海伦收集的样本数据主要包含以下3种特征：

• 每年获得的飞行常客里程数
• 玩视频游戏所消耗时间百分比
• 每周消费的冰淇淋公升数

打开txt文本文件，数据格式如下图所示：

准备数据：数据解析

将待处理的数据的格式改变为分类器可以接收的格式。

分类器接收的数据是什么格式的？从上小结已经知道，要将数据分类两部分，即特征矩阵和对应的分类标签向量。

得到的数据解析结果如下：

然后就可以通过友好、直观的图形化的方式观察数据

分析数据：数据可视化

导入matplotlib， 编写名为showDatas的函数，用来将数据可视化：

"""
Parameters:
    datingDataMat - 特征矩阵
    datingLabels - 分类Label
Returns:
    无
"""
def showDatas(datingDataMat, datingLabels):
    #设置汉字格式
    font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
    #将fig画布分隔成1行1列,不共享x轴和y轴,fig画布的大小为(13,8)
    #当nrow=2,nclos=2时,代表fig画布被分为四个区域,axs[0][0]表示第一行第一个区域
    fig, axs = plt.subplots(nrows=2, ncols=2,sharex=False, sharey=False, figsize=(13,8))
    numberOfLabels = len(datingLabels)
    LabelsColors = []
    for i in datingLabels:
        if i == 1:
            LabelsColors.append('black')
        if i == 2:
            LabelsColors.append('orange')
        if i == 3:
            LabelsColors.append('red')
    #画出散点图,以datingDataMat矩阵的第一(飞行常客例程)、第二列(玩游戏)数据画散点数据,散点大小为15,透明度为0.5
    axs[0][0].scatter(x=datingDataMat[:,0], y=datingDataMat[:,1], color=LabelsColors,s=15, alpha=.5)
    #设置标题,x轴label,y轴label
    axs0_title_text = axs[0][0].set_title(u'每年获得的飞行常客里程数与玩视频游戏所消耗时间占比',FontProperties=font)
    axs0_xlabel_text = axs[0][0].set_xlabel(u'每年获得的飞行常客里程数',FontProperties=font)
    axs0_ylabel_text = axs[0][0].set_ylabel(u'玩视频游戏所消耗时间占',FontProperties=font)
    plt.setp(axs0_title_text, size=9, weight='bold', color='red') 
    plt.setp(axs0_xlabel_text, size=7, weight='bold', color='black') 
    plt.setp(axs0_ylabel_text, size=7, weight='bold', color='black')
 
    #画出散点图,以datingDataMat矩阵的第一(飞行常客例程)、第三列(冰激凌)数据画散点数据,散点大小为15,透明度为0.5
    axs[0][1].scatter(x=datingDataMat[:,0], y=datingDataMat[:,2], color=LabelsColors,s=15, alpha=.5)
    #设置标题,x轴label,y轴label
    axs1_title_text = axs[0][1].set_title(u'每年获得的飞行常客里程数与每周消费的冰激淋公升数',FontProperties=font)
    axs1_xlabel_text = axs[0][1].set_xlabel(u'每年获得的飞行常客里程数',FontProperties=font)
    axs1_ylabel_text = axs[0][1].set_ylabel(u'每周消费的冰激淋公升数',FontProperties=font)
    plt.setp(axs1_title_text, size=9, weight='bold', color='red') 
    plt.setp(axs1_xlabel_text, size=7, weight='bold', color='black') 
    plt.setp(axs1_ylabel_text, size=7, weight='bold', color='black')
 
    #画出散点图,以datingDataMat矩阵的第二(玩游戏)、第三列(冰激凌)数据画散点数据,散点大小为15,透明度为0.5
    axs[1][0].scatter(x=datingDataMat[:,1], y=datingDataMat[:,2], color=LabelsColors,s=15, alpha=.5)
    #设置标题,x轴label,y轴label
    axs2_title_text = axs[1][0].set_title(u'玩视频游戏所消耗时间占比与每周消费的冰激淋公升数',FontProperties=font)
    axs2_xlabel_text = axs[1][0].set_xlabel(u'玩视频游戏所消耗时间占比',FontProperties=font)
    axs2_ylabel_text = axs[1][0].set_ylabel(u'每周消费的冰激淋公升数',FontProperties=font)
    plt.setp(axs2_title_text, size=9, weight='bold', color='red') 
    plt.setp(axs2_xlabel_text, size=7, weight='bold', color='black') 
    plt.setp(axs2_ylabel_text, size=7, weight='bold', color='black')
    #设置图例
    didntLike = mlines.Line2D([], [], color='black', marker='.',
                      markersize=6, label='didntLike')
    smallDoses = mlines.Line2D([], [], color='orange', marker='.',
                      markersize=6, label='smallDoses')
    largeDoses = mlines.Line2D([], [], color='red', marker='.',
                      markersize=6, label='largeDoses')
    #添加图例
    axs[0][0].legend(handles=[didntLike,smallDoses,largeDoses])
    axs[0][1].legend(handles=[didntLike,smallDoses,largeDoses])
    axs[1][0].legend(handles=[didntLike,smallDoses,largeDoses])
    #显示图片
    plt.show()

可视化结果如下所示：

通过数据可以很直观的发现数据的规律，比如以玩游戏所消耗时间占比与每年获得的飞行常客里程数，只考虑这二维的特征信息，给我的感觉就是海伦喜欢有生活质量的男人。为什么这么说呢？每年获得的飞行常客里程数表明，海伦喜欢能享受飞行常客奖励计划的男人，但是不能经常坐飞机，疲于奔波，满世界飞。同时，这个男人也要玩视频游戏，并且占一定时间比例。能到处飞，又能经常玩游戏的男人是什么样的男人？很显然，有生活质量，并且生活悠闲的人。我的分析，仅仅是通过可视化的数据总结的个人看法。我想，每个人的感受应该也是不尽相同。

准备数据：数据归一化

我们很容易发现，每年获取的飞行常客里程数对于计算结果的影响将远远大于表2.1中其他两个特征-玩视频游戏所耗时间占比和每周消费冰淇淋公斤数的影响。而产生这种现象的唯一原因，仅仅是因为飞行常客里程数远大于其他特征值。但海伦认为这三种特征是同等重要的，因此作为三个等权重的特征之一，飞行常客里程数并不应该如此严重地影响到计算结果。

在处理这种不同取值范围的特征值时，我们通常采用的方法是将数值归一化，如将取值范围处理为０到１或者-１到１之间。比如，下面的公式可以将任意取值范围的特征值转化为０到１区间内的值，消除量纲影响：

newValue = (oldValue - min) / (max - min)

其中min和max分别是数据集中的最小特征值和最大特征值。虽然改变数值取值范围增加了分类器的复杂度，但为了得到准确结果，我们必须这样做。编写名为autoNorm的函数，用该函数自动将数据归一化。代码如下：

"""
Parameters:
    dataSet - 特征矩阵
Returns:
    normDataSet - 归一化后的特征矩阵
    ranges - 数据范围
    minVals - 数据最小值
"""
def autoNorm(dataSet):
    #获得数据的最小值
    minVals = dataSet.min(0)
    maxVals = dataSet.max(0)
    #最大值和最小值的范围
    ranges = maxVals - minVals
    #shape(dataSet)返回dataSet的矩阵行列数
    normDataSet = np.zeros(np.shape(dataSet))
    #返回dataSet的行数
    m = dataSet.shape[0]
    #原始值减去最小值
    normDataSet = dataSet - np.tile(minVals, (m, 1))
    #除以最大和最小值的差,得到归一化数据
    normDataSet = normDataSet / np.tile(ranges, (m, 1))
    #返回归一化数据结果,数据范围,最小值
    return normDataSet, ranges, minVals

normDataSet, ranges, minVals = autoNorm(datingDataMat)

行上述代码，得到结果如下：

我们已经顺利将数据归一化了，并且求出了数据的取值范围和数据的最小值，这两个值是在分类的时候需要用到的，直接先求解出来，也算是对数据预处理了

测试算法：验证分类器

评估算法的正确率，通常我们只提供已有数据的90%作为训练样本来训练分类器，而使用其余的10%数据去测试分类器，检测分类器的正确率。需要注意的是，10%的测试数据应该是随机选择的，由于海伦提供的数据并没有按照特定目的来排序，所以我们可以随意选择10%数据而不影响其随机性。KNN分类器：

"""
Parameters:
    inX - 用于分类的数据(测试集)
    dataSet - 用于训练的数据(训练集)
    labes - 分类标签
    k - kNN算法参数,选择距离最小的k个点
Returns:
    sortedClassCount[0][0] - 分类结果
"""
def classify0(inX, dataSet, labels, k):
    #numpy函数shape[0]返回dataSet的行数
    dataSetSize = dataSet.shape[0]
    #在列向量方向上重复inX共1次(横向),行向量方向上重复inX共dataSetSize次(纵向)
    diffMat = np.tile(inX, (dataSetSize, 1)) - dataSet
    #二维特征相减后平方
    sqDiffMat = diffMat**2
    #sum()所有元素相加,sum(0)列相加,sum(1)行相加
    sqDistances = sqDiffMat.sum(axis=1)
    #开方,计算出距离
    distances = sqDistances**0.5
    #返回distances中元素从小到大排序后的索引值
    sortedDistIndices = distances.argsort()
    #定一个记录类别次数的字典
    classCount = {}
    for i in range(k):
        #取出前k个元素的类别
        voteIlabel = labels[sortedDistIndices[i]]
        #dict.get(key,default=None),字典的get()方法,返回指定键的值,如果值不在字典中返回默认值。
        #计算类别次数
        classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
    #python3中用items()替换python2中的iteritems()
    #key=operator.itemgetter(1)根据字典的值进行排序
    #key=operator.itemgetter(0)根据字典的键进行排序
    #reverse降序排序字典
    sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
    #返回次数最多的类别,即所要分类的类别
    return sortedClassCount[0][0]

分类器测试函数：

""" 
Parameters:
    datingLabels：真实分类
    normMat：归一化后数据
    ranges：数据范围
    minVals：数据最小值
Returns:
    无 
"""
def datingClassTest(datingLabels,normMat, ranges, minVals):
    #取所有数据的百分之十
    hoRatio = 0.10
    #获得normMat的行数
    m = normMat.shape[0]
    #百分之十的测试数据的个数
    numTestVecs = int(m * hoRatio)
    #分类错误计数
    errorCount = 0.0
    
    for i in range(numTestVecs):
        #前numTestVecs个数据作为测试集,后m-numTestVecs个数据作为训练集
        classifierResult = classify0(normMat[i,:], normMat[numTestVecs:m,:],
            datingLabels[numTestVecs:m], 4)
        print("分类结果:%d\t真实类别:%d" % (classifierResult, datingLabels[i]))
        if classifierResult != datingLabels[i]:
            errorCount += 1.0
    print("错误率:%f%%" %(errorCount/float(numTestVecs)*100))

运行代码，测试结果如下：

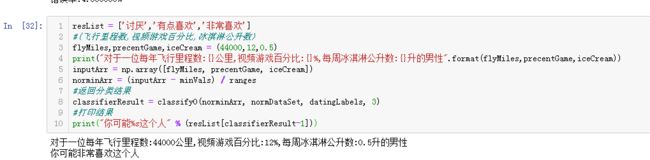
验证分类器结果中可以看出，错误率是4%，这是一个想当不错的结果。我们可以改变函数datingClassTest内变量hoRatio和分类器k的值，检测错误率是否随着变量值的变化而增加。依赖于分类算法、数据集和程序设置，分类器的输出结果可能有很大的不同。

​

并输入数据(44000,12,0.5)，预测结果是"你可能非常喜欢这个人"，也就是这个人魅力一般。一共有三个档次：讨厌、有些喜欢、非常喜欢，对应着不喜欢的人、魅力一般的人、极具魅力的人