唠唠(信息熵)一大家子的事
唠唠(信息熵)一大家子的事
- 话说林舒是《信道编码》的大牛,最近在看大牛著作《信道编码:经典与现代》,同时也在《模式识别与机器学习》课堂,碰到了同一个理解不好的概念,那就是【熵】,真伤啊!
- 在码农界里,很多人在做自然语言处理NLP,这块也避免不了被【熵】一下。
- 来吧,哥们儿姐妹儿们,今天一起用人话,唠唠这烦人的【熵】。
本文参考于多位网上作者的文章总结整合而成,为尊重各位作者特此把参考地址列在文章结尾。
1. 用人话讲讲,何为“熵”?
你身边有没有废话特别多的人,有啊。有个奇葩室友每天都会告诉我:“明天太阳从东边升起来”。正常人一听,这不是废话呢嘛!说的这话一点信息量都没有,为什么呢,你不告诉我,太阳也是从东边升起,这事一点也不刺激。
1.1 信息量有多大?
那就要说道说道了,传递到的信息可以量化吗?
比如我们的学习成绩就可以量化,0-100分看你怎么考。那么信息的多少用什么量化呢,我们经常开玩笑说,这个人说的这句话信息量比较大。
信息的多少就叫做信息量。
那为什么有的信息量比较大,有的信息量就小呢。室友今天对着我发疯似的说了100遍:明天太阳从东边升起。我们会觉得这是废话,传递给我们的没有任何信息量。为什么呢,他传递来的消息事件在我们看来是确定的啊!
室友今天突然一反常态地告诉我:明天我们这儿要地震!正常人的第一反应是,我靠!真的假的?!要不要先做好预防措施。这句话比上面那句东方升起的太阳可太有信息量了。为什么呢,明天当地是否地震,谁也说不准,这个事件本身就是不确定的。
事件的不确定性决定了信息量的大小。
我们已经知道,信息量是由事件发生的不确定性决定的,不确定性越大,信息量越大。 但是不确定性又有什么衡量标准呢,换句话说,什么样的事件不确定性更大呢?
实验室几个朋友约好这个周末去看电影,到了那天,实验室的小王先到了电影院,已知电影院有 10 ∗ 10 = 100 10*10=100 10∗10=100 个位子,实验室小王的朋友也将过去,但他想知道小王坐在哪,这个时候小王的位置是有100种可能的,即可能性的结果是非常的多,不确定性也就越大。偏偏这个时候小王的朋友很了解小王的习惯,小王很喜欢在中间第三排的最左边位子看电影,一般情况下小王 99% 是要坐在那个位置的,这就意味着小王坐在其他位置的可能性微乎其微,这个时候可能性的结果受到概率的影响,使得别人传递再多小王相关的信息,我们也会觉得基本上用处不大,因为我们几乎确定小王的位置了。
不确定性的变化大小和两个因素相关:1. 可能的结果数目;2. 可能结果的概率。
那我们这个时候可以用数学公式来定义信息量了,信息量化的特点:
1。 非负数:信息量最多是没有,不可能对你说句话还能让你少知道点什么。
2。 可加性
3。 考虑两个因素
终于可以讨论信息熵了,信息熵是跟所有的可能性,以及每个可能事件的发生的概率有关的。
信息熵就是发生一个事件平均下来我们可以得到的信息量大小。所以数学上,信息熵其实是信息量的期望。
(1) H ( X ) = − ∑ i p ( x i ) ∗ l o g p ( x i ) H(X)=-\sum_{i}p(x_i)*log {p(x_i)}\tag1 H(X)=−i∑p(xi)∗logp(xi)(1)
这就是信息熵的定义,是我们本文的第一个公式。公式的函数设计都是满足了我们之前讨论的 信息量化的特点 的。公式里面的对数底数为什么是2?这是因为,我们只需要信息量满足低概率事件 X X X 对应于高的信息量,所以对数的选择是任意的。一般遵循信息论的普遍传统使用2作为底,这时信息量用 b i t bit bit 做单位。
1.2 联合熵/条件熵/互信息
- 联合熵
信息熵在联合概率分布的自然推广,就得到了联合熵。想一下,之前的信息熵只讨论一个事件 X X X ,联合熵针对的就是两个事件 X 1 X_1 X1 、 X 2 X_2 X2 的可能性分布。不再过多赘述。
KaTeX parse error: \tag works only in display equations
- 条件熵
条件熵是另一个变量 Y Y Y 的信息熵对 X X X(条件)的期望。假设 X X X有两种可能:我很帅;我不帅。对于 X = 我 很 帅 X = 我很帅 X=我很帅 下面 Y Y Y 的可能分布对应一种信息熵;对于 X = 我 不 帅 X = 我不帅 X=我不帅 下面 Y Y Y 的可能分布对应另一种信息熵。信息熵按照 X X X(条件)概率求期望。
KaTeX parse error: \tag works only in display equations
- 互信息(mutual information,MI)
原来我对 X X X 有些不确定(不确定性为 H ( X ) H(X) H(X) ),告诉我 Y Y Y 后我对 X X X 的不确定性变为 H ( X ∣ Y ) H(X|Y) H(X∣Y) ,这个 不确定性的减少量就是 X X X, Y Y Y之 间的互信息 。
(4) I ( X ; Y ) = H ( X ) − H ( X ∣ Y ) I(X;Y)=H(X)-H(X|Y) \tag4 I(X;Y)=H(X)−H(X∣Y)(4)
我们熟悉的香农公式,求信道容量的公式如下:
(5) C = max p ( x i ) I ( X ; Y ) C=\max_{p(x_i)}I(X;Y)\tag{5} C=p(xi)maxI(X;Y)(5)
信道输入是 X X X,输出接收是 Y Y Y,将输出接收译为 X ^ \hat{X} X^。信道容量是在对应的输入 X X X 分布下最大的互信息。
2. 交叉熵
2.1 信息熵的作用
比如唐僧四师徒(**唐僧、孙悟空、猪八戒、沙僧**)西天取到真经,回到东土大唐。唐王李世民想尽快看看佛经,但是唐僧师徒有个条件,就是唐僧四师徒进行一场赛跑;唐王最早猜出谁会跑第一名胜出,就可以尽早得到佛经。我们把这**四位师徒**记作 { A, B, C, D }。**谁会跑第一名胜出这个事件**记为随机变量 $X$ 属于 { A, B, C, D } 。 这个问题实质上就转化为:我们需要用**尽可能少的猜测策略**来确定随机变量 $X$ 的取值,这里的猜测形式可以是**任意的二元问题**(是/不是)来得到真实的回馈。 如果你现在是唐王,你对四位的**任何关于实力的信息都不知道**。 你肯定先假设的是四位 A、B、C、D 胜出的概率相当,获胜概率分别为 { 1/4, 1/4, 1/4, 1/4 }。 最后我们可以预期通过以下的**直线(傻瓜)式策略**来确定取值: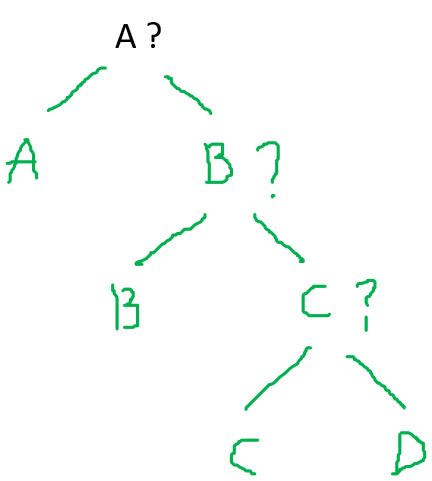
假设我们一共猜测了 N N N 次猜对的。这个策略下我们猜的次数的期望是多少呢?
(6) E ( N ) = 1 4 ⋅ ( 1 + 2 + 3 + 3 ) = 9 4 \mathbb{E}(N)=\frac{1}{4}\cdot (1+2+3+3)=\frac{9}{4}\tag{6} E(N)=41⋅(1+2+3+3)=49(6)
显然,根据我们的概率论基础知识,最好的策略一定 对应于 最小的期望。这其实就是我们熟知的哈夫曼编码的目的。
其实,上面的公式类似于信息熵公式,但不是信息熵!在这里 次 数 = − l o g 2 ( p i ) 次数=-log_2(p_i) 次数=−log2(pi)并不成立,原因是上述策略并不是哈夫曼编码结构。
首先我们在这里要明确一个问题,我们的猜测其实含有推理的成分,也就是说我们是可以提问推理的!二元问题可以进行有技巧的改进。让我们用哈夫曼编码的思想改动一下上面的策略来确定取值:
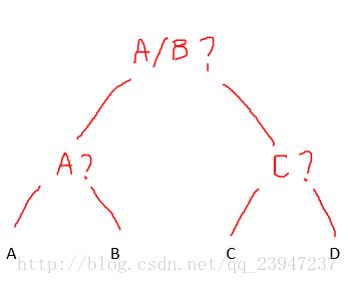
这个改进策略下我们猜的次数的期望是多少呢?
(7) E ( N ) = 1 4 ⋅ ( 2 + 2 + 2 + 2 ) = 8 4 \mathbb{E}(N)=\frac{1}{4}\cdot (2+2+2+2)=\frac{8}{4}\tag{7} E(N)=41⋅(2+2+2+2)=48(7)
显然按照这种二元问题步骤,只需要两步就可以完全确定A/B/C/D,该策略的期望优于直线式策略。
上面的公式就是信息熵公式。在这里 次 数 = − l o g 2 ( p i ) = l o g 2 ( 4 ) = 2 次数=-log_2(p_i)=log_2(4)=2 次数=−log2(pi)=log2(4)=2成立。这是基于假设等概情况下的信息熵。
2.2 从信息熵到交叉熵
如果你现在是唐王,其实你对四位高僧的实力信息是了解的。 毕竟西天取经九九八十一难后如来佛祖已经给他们师徒册封转正了,按照佛教地位的高低首先可以肯定他们的法力高低,法力高的自然胜出概率大。四位 A、B、C、D 获胜的概率分别为 { 1/2, 1/4, 1/8, 1/8 }。
让我们用哈夫曼编码的思想设计以下策略来确定取值:
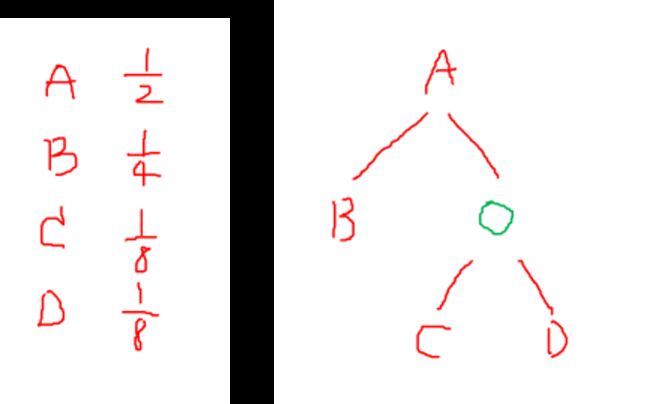
这个策略下我们猜的次数的期望是多少呢?
(8) E ( N ) = 1 2 ⋅ 1 + 1 4 ⋅ 2 + 1 8 ⋅ 3 ⋅ 2 = 7 4 \mathbb{E}(N)=\frac{1}{2}\cdot 1+\frac{1}{4}\cdot 2+\frac{1}{8}\cdot 3\cdot2=\frac{7}{4}\tag{8} E(N)=21⋅1+41⋅2+81⋅3⋅2=47(8)
这时我们知道了各种概率,由于A占比1/2,如果先猜A,很大可能第一次就猜对了。所以,1/2的概率是A需要猜一次,1/4的概率是B需要猜两次,1/8的概率是C需要猜三次,1/8的概率是D需要猜三次。
由于我们举得例子不太好,这个策略和直线式策略看起来结构是一样的,但是注意我们的最佳策略是根据概率和哈夫曼原理生成的。所以说大家不需要多想,因为接下来我们关注的是怎么理解交叉熵。
式(7)和(8)作比较。
我们知道了 A、B、C、D 的真实概率分布是 { 1/2, 1/4, 1/8, 1/8 }。
式(7)计算的熵代表了我们在完全不了解真实概率分布策略下的猜测次数的期望,相当于我们为消除不确定性而付出的代价,这个时候代价为 8/4 次。而根据真实分布,我们要付出式(8)所示的 7/4 次的代价来确定。显然对于分布 { 1/2, 1/4, 1/8, 1/8 } 来说,式(7)的哈夫曼结构是忽略了真实分布的信息而认为分布是先验等概的,自然不如式(8)的哈夫曼结构。
可见,基于真实分布的信息熵的结构策略是最优的。
但是,实际中很多时候我们对待测的事件的真实分布总是知之有限,所以实际中大多数情况下都是在用(非真实分布的)非最优策略去消除系统的不确定性。
那么当我们使用非最优策略消除系统的不确定性,所需要付出的代价如何去衡量呢?
这就需要引入交叉熵,用来衡量在给定的真实分布下,使用非真实分布所指定的策略消除系统的不确定性所需要付出的代价。
如例子中事件 X X X 的分布如下
真实分布 p k p_k pk ={ 1/2, 1/4, 1/8, 1/8 }
非真实分布 q k q_k qk ={ 1/4, 1/4, 1/4, 1/4 }
交叉熵定义:
(9) H ( p , q ) = − ∑ k p k log 2 q k H(p,q)=-\sum\limits_{k} p_k\log_2 q_k\tag{9} H(p,q)=−k∑pklog2qk(9)
在例子中的交叉熵有多大呢?
(10) H ( p , q ) = 1 2 ⋅ 2 + 1 4 ⋅ 2 + 1 8 ⋅ 2 + 1 8 ⋅ 2 = 8 4 H(p,q)=\frac{1}{2}\cdot 2+\frac{1}{4}\cdot 2+\frac{1}{8}\cdot 2+\frac{1}{8}\cdot 2=\frac{8}{4}\tag{10} H(p,q)=21⋅2+41⋅2+81⋅2+81⋅2=48(10)
交叉熵算出的代价为 8/4,已知最优策略如式(8)的代价为7/4,可见 8 4 > 7 4 \frac{8}{4}>\frac{7}{4} 48>47。
因此交叉熵越低,策略就越好,最低的交叉熵也就是使用了真实分布所计算出来的信息熵。
在Machine Learning的分类算法中,我们总是最小化交叉熵代价的原因就是交叉熵越低,就证明由算法所产生的策略最接近最优策略,也间接证明我们算法所算出的非真实分布越接近真实分布。
3. 相对熵
- 如果你已经很好掌握了信息熵和交叉熵的概念,相对熵的理解自然就水到渠成了。
- 上面我们分析到了概率分布下的不同策略,这些策略放到具体领域比如就是一些编码算法。我们在上文分析的是非最优策略和真实分布下的最优策略之间的关系。
- 最后,我们不妨分析的再彻底一点!去衡量不同策略之间的差异。这就需要用到相对熵,用来衡量两个取值为正的函数(或概率分布)之间的差异。
相对熵 定义:
(11) K L ( p ∣ ∣ q ) = ∑ k p k log 2 p k q k KL(p||q)=\sum\limits_{k} p_k\log_2 \frac{p_k}{q_k}\tag{11} KL(p∣∣q)=k∑pklog2qkpk(11)
- 现在,我们就计算一下式(7)、式(8)之间的差异,相对熵 闪亮登场!
K L ( p ∣ ∣ q ) = ∑ k p k log 2 p k q k KL(p||q)=\sum\limits_{k} p_k\log_2 \frac{p_k}{q_k} KL(p∣∣q)=k∑pklog2qkpk
(12) = ∑ k p k log 1 q k − ∑ k p k log 1 p k =\sum\limits_{k} p_k\log \frac{1}{q_k}-\sum\limits_{k} p_k\log \frac{1}{p_k}\tag{12} =k∑pklogqk1−k∑pklogpk1(12)
(13) = H ( p , q ) − H ( p ) =H(p,q)-H(p)\tag{13} =H(p,q)−H(p)(13)
可知,
相对熵 = 交叉熵 - 信息熵(真实分布的最优策略)。
K L ( p ∣ ∣ q ) = H ( p , q ) − H ( p ) = 8 4 − 7 4 = 1 4 KL(p||q)=H(p,q)-H(p)=\frac{8}{4}-\frac{7}{4}=\frac{1}{4} KL(p∣∣q)=H(p,q)−H(p)=48−47=41
-
写博客真累,but,分享是一个很快乐的过程。
-
丁不四在临行侠客岛前对爱慕已久的史小翠说:算了,喜欢一个人嘛,看一眼是如此,过一辈子也是如此!
感觉他说的直指人心啊,甚有道理!
很多情况下,我们觉得吃的要追求,穿的要追求;其实,一日三餐,粗茶淡饭亦是如此,山珍海味亦是如此,有何分别呢。
只想说现在还有像我一样注重精神世界的人吗,说这话感觉怪怪的还是不说了吧,妥妥的先做好自己的分内事吧。
参考出处:
【1】https://www.zhihu.com/question/41252833/answer/195901726
【2】http://www.amazingcomm.com/
【3】https://www.zhihu.com/question/22178202/answer/49929786
【4】http://www.cnblogs.com/liaohuiqiang/p/7673681.html