愉快的清北之旅（并不！

带着未完的作业，我开始了新的旅程 = =
不说闲话了…但似乎除了闲话也没什么好说的？（雾

目录

Day 1 简单的算法

---

调整法

　　似乎是一种奇妙的题面处理法，通过分治讨论或一些奇妙的性质将题面简化或处理的更直观一点。

　【例题】最大乘积 P1249
　　　该题可用分治判断出４以上可再分，４一下不可分，８＜９等性质。

　【例题】ＨＤＵ color the chessboard 6122
　该题属棋盘类，可用通用棋盘调整，将（i+j）为奇数的格子翻转，可得特殊性质
　该题调整后会发现合法时对角线

Day 2 并不简单的算法

---

这些算法可以深究，非常非常深 _ 题记

背包优化

　　背包优化水很深，常见的有滚动数组和bitset模拟数组
　　其中bitset的核心是压维，然后用二进制的操作处理状态的转移
　　【例题】n个正整数，和不超过C，现要将其分成两部分使得和尽可
　　　　　　能接近，求最小差值， n和C规模相同，每个数不同。
　　　　　　
　　　　　　该题首先可以想到是个01背包，用f[i][j]表示选出前i个数中
　　　　　　的某些数之和是否等于j,c[i]表示第i个数
　　　　　　求出转移方程 ，即对选第i个数与不选第i个数取并，
　　　　　　转移方程：
　　　　　　f[i][j]=f[i]-1[j] | f[i-1][j-c[i]];
　　　　　　然后找到一个 f[n][x]=1，且x尽可能接近c/2
　　　　　　注：此处可视为n个数的总和为c

　　　　　　 此处可以用bitset优化，
　　　　　　 bitset< maxn >;
　　　　　　 f[i]=f[i-1] | (f[i-1]>>c[i]);
　　　　　　 复杂度O(n*c)+1/64注：1/64为lowbit常数
　　　　　　
　　　【例题】上题题面改为n个正整数，和不超过C，现要将其分成两
　　　　　　　部分使得和尽可能接近，求n个数中不同的数最多有多少个

　　　　　　要使不同的数尽可能多，所以只要让这些数尽可能小 ( n=C
　　　　　　时 所有数都等于1)
　　　　　　不同的数最多是sqrt(n)级别的
　　　　　　设第i件有d[i]个
　　　　　　题目转化为多重背包问题
　　　　　　dp[i][j]表示前i个数选出某些数，加起来能否等于j

　　　　　　
　　　　　　for(int i=0;i<=m;i++)
　　　　　　　　for(int j=0;j<=c;j++)
　　　　　　 　　　　for(int k=0;k<=d[i];k++)
　 　　　　　　　　　　　if(j+k*c[i]<=c)
　　　　　　　　　　　　　　　dp[i+1][j+k*c[i]] |= dp[i][j];
　　　　　　
　　　　　　这是最裸的dp了，不过我们可以对此优化
　　　　　　dp[i][j]表示前i个数选出一些数和为j最少使用几个c[i]
　　　　　　不合法初值赋-1即可
　　　　　　If(dp[i][j]
　　　　　　dp[i][j+c[i]]=min(dp[i][j+c[i]],dp[i][j]+1);
　　　　　
　　　　　　复杂度O(n^1.5);不太理想，不过水个100,000还是可以的
　　　　　　继续优化，利用二进制拆分，将其转化为01背包，套用前文
　　　　　　的bitset优化，可将复杂度降为n^0.5*O(logn)
　　　　　　可过1000,000

Day3 快乐的线段树

---

以及并不快乐的主席树__题记

【例题】[POI2005]SAM-Toy Cars P3419 这题根线段树似乎没什么关系= =
　　　贪心，拿走的玩具应尽晚被用，用堆维护地板上的玩具，水题一道

线段树维护前缀和

【例题】[HNOI2011]括号修复 / [JSOI2011]括号序列 P3215
　　　我做的是个简化版，只求整体序列是否合法和某一子串合不合法
　　　“(“为1 、”)”为-1，然后用线段树维护前缀和
　　　合法条件如下:
　　　1、左在右前，即整个序列最小前缀和>=0
　　　2、左右相等，即整个序列前缀和==0
　　　如果查询子串，则(sum[i] (l<=i<=r) >=sum[l-1] && sum[r]-sum[l]==0)

用线段树维护序列，单独处理区间

【例题】[NOI2016]区间 P1712
　　　本来想今晚打出来，想来想去还是选择了主席树（毕竟今晚是J主席生日
　　　由于要求最小，先把各区间按长度从小到大排序
　　　模拟两个指针i j，用for使指针i右移（因为最优解需要区间最小长度最大）
　　　每当i右移，都可能使原解不合法（删掉的可能刚好覆盖x点），若如此，j都需要
　　　不断右移直到某个点的覆盖次数==m（说明出现合法解，但不一定最优），再
　　　更新ans（取min）
　　　细节：注意i右移完了，需要删掉原来的覆盖。若j>n说明当前i及i以后的区间都
　　　不能有解，直接break
　　　写个伪代码，免得忘了= =

modify(l,r,dlt);//区间修改
check();//区间查询最大值是否==m
l[],r[];//下标区间的左右端点

for(int i=1;i<=n;i++)
{
    if(i>1)
        modify(l[i-1],r[i-1],-1);//删掉移走的覆盖
    while(j<=n && !check())//右移j寻找新解
    {
        j++;
        if(j<=n)
            modify(l[j],r[j],1);
    }
    if(j>n)
        break;//老娘不伺候你们了
    ans=min(ans,(r[j]-l[j])-(r[i]-l[i]));
    }
}

线段树扫描线

【例题】线段树扫描线 T25008
　　不会，待续

线段树维护最大连续区间

【例题】[USACO08FEB]酒店Hotel P2894
　　待续

Day 3.5 悲伤的主席树

---

特殊的日子种特殊的树_题记 from 8.17

插句题外话，主席树是现学的，所以就写的详细点，以备复习之需

前置知识点：离散化

很多时候对于巨大数据，我们并不在意他们的具体数值，只在意其“相对大小”（即排序后的下标），因此我们可以进行离散化来防止数组越界
其实我也很好奇为什么一个压缩数范围的算法要叫“离散化”

//unique(u,v)返回去重(伪)后的地址，被删掉的会加到返回值后
//bo==lower_bound(u,v,x)返回最接近x的值的地址
int const maxn=1e5+10;
int a[maxn], t[maxn];
int n;
scanf("%d",&n);
for(int i=1; i<=n; i++)
    scanf("%d",a[i]),t[i]=a[i];
sort(t+1,t+n+1);//排序，找相对大小
m=unique(t+1,t+1+n)-t-1;//m为不重复的元素的个数
for(int i=1; i<=n; i++)
    a[i]=lower_bound(t+1,t+1+m,a[i])-t;//相对大小的

主席树实现原理

主席树是个乱搞的产物，他是为了解决区间第k小/大问题而诞生的（然后虐了老大哥划分树
最朴素的求区间第k小/大数的方法显然是暴力取出所有值然后排个序
介于用线段树维护区间的优良传统，我们考虑用线段树进行优化
第k小显然难以直接维护，考先虑优化排序，怎么才能尽量快用线段树完成排序呢？

很容易想到离散化找相对大小
然后把相对大小当成区间的端点，用线段树的节点存储l,r出现数的次数，这样对于l,r的区间，只要每当l,mid的值<=k就向左子树走，否则往右走，即可找到k小

然而马上就会发现自己毕竟还是too young，由于只对于l,r的区间离散，所以每次查询都要开一个新线段树，然后时空同时gg
(待续)

主席树的实现代码

！这个代码还没调完，慎用

#include
#include
#include
using namespace std;

int const maxn=200100;

struct node
{
    int sum,lc,rc; 
}
t[maxn*20];//空间复杂度是nlogn，所以此处*log

int a[maxn],b[maxn];
int root[maxn],cnt;

inline void ins(int &u,int l,int r,int x)
{
    int now=++cnt;
    t[now]=t[u];
    //继承原树
    //这个地方是主席树的核心操作，每次加一个新点时，都建一棵新树，但保留之前共有的部分
    //如此一来，每棵树其实就具有了前缀和的性质
    if(l==r)
    {
        t[now].sum++;
        return;
    }
    int mid=(l+r)>>1;
    if(x<=mid)
        ins(t[now].lc,l,mid,x);
    else 
        ins(t[now].rc,mid+1,r,x);
    t[now].sum=t[t[now].lc].sum+t[t[now].rc].sum;
}

int inline query(int pre1,int pre2,int l,int r,int k)//pre1 pre2是进行前缀和差分的两棵树
{//l,r给定查询的区间
    if(l==r)
        return l;
    int m = t[t[pre2].lc].sum-t[t[pre1].lc].sum;
    //将对应的节点相减，就是l,r某个范围中的数的个数
    int mid=(l+r)>>1;
    if(k<=mid)
            return query(t[pre1].lc,t[pre2].lc,l,mid,k);
    return query(t[pre1].rc,t[pre2].rc,mid+1,l,k-m);
}
int main()
{
    int n,q;
    scanf("%d%d",&n,&q);
    for(int i=1;i<=n;i++)
        scanf("%d",a[i]),
        b[i]=a[i];
    sort(b+1,b+n+1);
    b[0]=unique(b+1,b+1+n)-b-1;//省4个字节的空间，血赚
    for(int i=1;i<=n;i++)
        a[i]=lower_bound(b+1,b+1+b[0],a[i])-b[0];
    root[0]=0;
    for(int i=1;i<=n;i++)
    {
        root[i]=root[i-1];
        ins(root[i],1,b[0],a[i]);
    }
    for(int i=1;i<=q;i++)
    {
        int l,r,k;
        scanf("%d%d%d",&l,&r,&k);
        printf("%d",b[query(root[l-1],root[r],1,b[0],k)]);
    }
    return 0;
}

Day 4 看似数论，实则图论

---

花式建图欢乐多__题记

最小生成树

【例题】[APIO2008]免费道路 P3623
　　该题的简化版：先跑一遍kruskal处理图的联通，然后再跑一遍，0边不够k就继续
　　加，不连通就加1边，水题一道

二分答案

【例题】bzoj tree 2652
　　将所有白边权+x再跑kruskal，x越大生成树中的白边就越少
　　二分x，使白边数刚好<=need，若小于，直接加一条最小边权的白边即可
【例题】[HNOI2009]最小圈
　　将所有边权-x，如果存在正权环，则说明改环的平均权值>x
　　二分x + SPFA判正权环
　　水题

Floyd

【例题】[NOI2007]社交网络 P2047
　　一眼就看出来用floyd，关键在于求最短路长度的过程中需要用乘法原理更新最短
　　路条数即Cs,t
　　代码写的非常清新易懂，此不赘述

for(int k=1;k<=n;k++)
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
        {
            if(dis[i][j]>dis[i][k]+dis[k][j])
            {
                dis[i][j]=dis[i][k]+dis[k][j];
                num[i][j]=num[i][k]*num[k][j];
                continue;
            }
            if(dis[i][j]=dis[i][k]+dis[k][j])
                num[i][j]+=num[i][k]*num[k][j];
        }       

　　至于Cs,t(v)，很容易想到经过 v 从 s 到 t 的最短路条数是以v为中间点的条数之
　　积
　　即ans[v]=num[i][v]*num[v][j]

【例题】[JSOI2007]合金 P4049
　　floyd找最小环+解析几何
　　然而我并不会解析几何
　　所以只能发出了咕咕咕的声音

Day 5 看似动规，实则图论

---

终有一日

当我放弃之时

(md老子做不动了)

DP会打破DAG的樊笼

状态为点转移为边

万物皆图论__题记

数位dp

数位dp就是对一个数字的位数进行操作的dp，一般用来统计区间(l,r)种满足条件的数的个数，状态的转移就是枚举下一位数

他有两个最基本的特征：

不满足区间减法 ，很显然知道不同位数的信息根本没啥用

有上下界限制，即枚举的数不能超出(l,r)区间

举例，求区间(l,r)有几个数
我们当然知道有r-l+1个数
不过不妨用数位dp的思想考虑一下做法
定义f[i][j][k]表示大到小的第i位有几个数,jk为0/1,表示是否<=r<=l
for(int i=l;i<=n;i++)
if()
【例题】求区间(l,r)的和
　　　　求区间(l,r)的最大值
　　　　bzoj 4737
　　　　P2822

树形dp

f[i]存储以i为根的字数的信息
f[i]=1+∑f（儿子）
由深度大的点想深度小的点更新信息
【例题】n个点的树，求有多少个点、最大点权，树的直径（树的最长简单路）

状压dp

实质是将一行状态压成一个数
f[i]表示选择集合的价值
枚举子集的方法

for(int i=1;i<(i<for(int j=1;j//枚举属于i的全部子集
        f[i]=merge(f[j],f[i^j]);

O(4^n) n<=14
玄学优化过后

for(int i=1;i<(1<i++)
    for(int j=a;j;j=(a-1)&a)
        f[i]=merge(f[j],f[i^j]);

O(3^n n<=18
枚举加某个数

for(int i=1;i<(1<i++)
    for(int j=1;j<=n;j++)
        if(a&(1<<(b-1)))
            f[a^(1<<(b-1))]-->f[a];

博弈论dp

博弈论dp状态的转移是由当前方转移为对方
若能转移到必败态，说明当前是必胜态
后手常用策略：对称性
博弈论的dp一般称为sg函数，必败态sg==0
设mex()为找未出现的最小自然数
sg(0)=0;
sg(x)=∑(i=1,x-1) mex()
SG定理：复合游戏的sg值=每个字游戏的sg值的抑或和
其实做平等博弈问题的关键就是把题面转化为最简单的nim游戏
例如
【例题】CodeChef SHGAME
n*m的网格图中有一个(x,y)的格子被染成黑色，双方可轮流把网格二分，保留黑子的一边，当前无法操作者输，求有多少个(x,y)能使先手必胜，N,M<=10^6

观察一下不难发现，这其实是个4堆石子的nim游戏…
【例题】HDU 4317
^:不进位加法
思考题目
后手赢的条件是石头的^值为0，即每位需要偶数个1
得到偶数1的
f[i][s]表示从最高位到i位的^值为0且集合s需要进位 所需的石头数
然后全程掉线

背包dp

【例题】CodeChef APRIL14 ANUCBC
n个数字，选出其一个子集。 求有多少子集满足其中数字之和是m的倍数。n ≤ 100000，m ≤ 100

一个数列取模后可看作一个val<=模数的多重背包
但看似相同的数取模前是不同的，因此他们所代表的方案数就不同

组合数dp

一般与方案数统计有关的dp都与组合数有关，即转移过程中往往要乘上组合数

【例题】TC SRM 498 Div1 1000PT
网格中每步可以走(0……Mx,0……My)中任意非零向量
有K种向量不能走
分别是(ki,ki) ki一定是10的倍数
求从(0,0)走到(Tx,Ty)的方案数
Tx,Ty,Mx,My<=800,R<=1600,K<=50

f[k][i][j]表示走k步到i,j
最朴素的转移

for (int i=1;i<=dx;i++)
    for (int j=1j<=dy;j++)
        if(can(dx)&&can(dy))
            f[k+1][i+dx][j+dy]+=f[k][i][j];

g[i][a]走i步，只走不合法，走到(10a，10a)的方案数
运用容斥原理，至少走0步不合法-至少走一步不合法+至少走两步不合法….=走0步不合法
f[r][tx][ty] - ∑ (1-a)g[1][a]*f[r-1][tx-10a][ty-10a]*c(1,r)+…….
【例题】BZOJ 1801
在n*m的棋盘上放若干个炮使其不互相攻击
若不互相攻击，显然行列上都至多有2个炮
因此用f[i][j][k]表示前i行已放好，有j列0炮，有k列1炮，有m-k-j列2炮的方案数
常见维度优化：可优化的维度用其他维度表示
状态转移如下
下一行不放炮:
f[i+1][j][k]+=f[i][j][k];
下一行放一炮:
f[i+1][j-1][k+1]+=f[i][j][k]*C(j,1)
下一行放两炮:
f[i+1][j][k+1]+=f[i][j][k]*C(k,1);

【例题】CC FEB14 LEMOVE
给定一个有N个点的图，每个点都向外连出一条有向边，边长均为1。现 要求在图中添加尽量少的从1号点出发的边，使得1号节点到每个节点的距离 都不超过K。 求添加的最少边数。N ≤ 100000

f[i][j]表示第i种 激动值为j的方案数
首先把数从大到小排序+去重，然后把数插入
为什么要从大到小排呢
因为这样才能保证激动值不会减小，而且当且仅当新插入的数在数列首时，激动值++
于是找到状态f[i][j]代表填入前i个数（即前i大）能产生的j的激动值的方案数
每次转移方程要*方案数 y!*C(x+y-1,y-1)

【例题】
n个数，有n！种排列，把每种排列视为一个数，求这n!个数中有多少个11的倍数
n<=50,a[i]<=1e9;

1.一个数奇数位的和-偶数位的和=(11的倍数 | 0)，则该数为11的倍数
2.(奇和-偶合)%11==原数%11
f[i][j]表示插入i个数，%11==j的方案数
朴素的想法:
如果插入的数是偶数位，则右侧的奇偶不变，f[i+1][j+a[i]%11]+=f[i][j];
若奇数位,则右侧奇偶互换,然后无法求左右奇偶和，gg
不妨单独处理奇数位的数
g[i][j][k][l]已经放好了前i个奇数位的数，j在奇数位开头，k在偶数位开头,%11为l的方案数
然后就掉线了

【例题】P1057的魔改版
题目大意：一群人一个环，每个人向左传球的概率为p[i]，向右传的概率为1-p[i]，求使所有人接到球的最大概率

f[l][r][0/1]表示l,r中的人被标记时，球在l,r的概率是多少(0表示球在l处，1表在r处)
if(l+1==r)显然该区间只覆盖一个点，其向左传的概率为pi
思考两个点
由于球可能会无限传递，可得出式子pp=(1-p[1])p[2](1-p[1])*…
然后用无限项等比数列求和求出向左传的概率，作为把他们看成一个点时向左传的概率
时间复杂度是O(n^3)
似乎是这样…
因为我掉线了…
听说有O(n)的图论做法…
然而我不会…

射线法dp

【例题】CF375c Circling Round Treasures
判断一个点是否在多边形内部：
向一个方向作射线，若与多边形的交点为奇数，则在内部，若交点为偶数，则在外部

常见dp优化方法

四边形不等式
斜率优化
单调性优化
矩阵乘法+快速幂（将n优化为logn）
滚动数组优化
数据结构优化

Day 6 字符串太太太超纲啦

“kmp难教难学”

“抱歉，双模哈希真的可以为所欲为”——题记

Manacher马拉车算法

【练习题】 P3805 P3454
该算法可线性求字符串的最长回文串和每个位置为中心的回文串长度
具体实现如下
先找到右端点最靠右的回文串的中心m
1、若以i为中心的回文串在m串内
根据对称性
f[i]=f[2m-i];
2、若不完全在m内
3、完全不在m内

inline void manacher (char *s)
{
    int l=strlen(s+1);
    f[1]=1;
    int nowmid=1,nowright=1;
    for (int a=2;a<=n;a++)
    {
        if (a<=nowright)
        {
            int p=2*nowmid-a;
            f[a]=min(f[p],2*(nowright-a)+1);
        }
        else f[a]=1;
        int x=f[a]/2;
        while (a-x-1>=1&&a+x+1<=l&&s[a-x-1]==s[a+x+1])
        {
            x++;
            f[a]+=2;
        }
        if (a+x>nowright)
        {
            nowright=a+x;
            nowmid=a;
        }
    }
}

以上代码只能求出长度为奇数的回文串，因为该算法需要找中心
因此不妨插入一些无意义的字符作为虚点

Z-Box 扩展KMP

字符串的后缀数=字符串长度
f[i]表示第i个后缀与原串的最长匹配长度(每一位相同，长度++，直到有一位无法匹配)
f[1]=len;
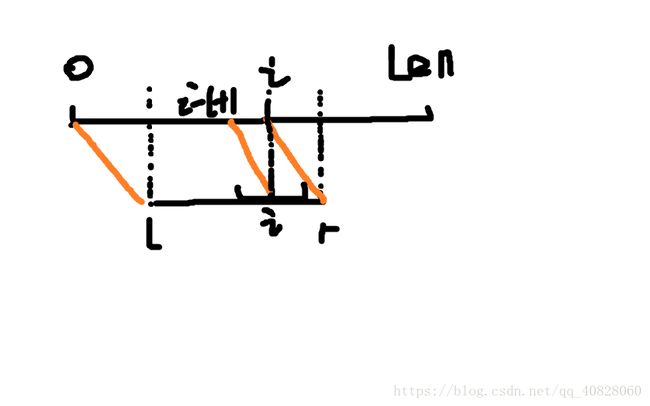
从匹配上的字符串找一个右端点最靠右的字符串(l,r)
可发现(l,r,0,len)可构成平行四边形
f[i]=f[i-(l-1)]=f[i-l+1];
如图所示

顺便说一下
kmp的next[]与ZBox的f[]的和=原串长度
所以
len-f[]=next[];
然后就可以用ZBox水过KMP的模板题啦

哈希 hash

模数p的应有的性质

1.是质数，质数能保证%完后1-p的
2.约等于10^9，较大少冲突，平方不会爆 long long
3.别用常用质数(1e9+7)

单模哈希 hash

f(s)//将字符串变为一个27进制的int
g(s)=f(s)%p

双模hash

放心吧不会被卡

自然溢出法

爆 unsigned long long 相当于 (p=2^64)

三种hash的选择

1、随机数据的正确率(双模>自然溢出>单模)
2、卡模数的正确率(双模>单模>自然溢出)
3、速度(自然溢出>单模>双模)

综上
卡常=自然溢出
卡模数=双模
卡常+卡模数=单模

【例题】
bzoj 3097~3099 hash killer
用hash写manacher

O(1)计算子串的hash

base是一个10,000左右的奇数
bit(i)表示base^i,h()存前缀hash值,可据此o(1)算子串hash值
通过类似前缀和来实现

get(int l,int r)
{
    h[r]-h[l-1]*bit[r-l+1];
}

Day 7 数论太太太超模啦

矩阵乘法

矩阵乘法就是把第一个矩阵的第i行中每个数乘上第二个矩阵的第j列中每个数的和记录在c[i][j]

for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++)
        for(int k=1;k<=n;k++)
            c[i][j]+=a[i][k]*b[k][j];

另一种写法

for(int i=1;i<=n;i++)
    for(int k=1;k<=n;k++)
        for(int j=1;j<=n;j++)
            c[i][j]+=a[i][k]*b[k][j]

由此可知矩乘不满足交换律,满足结合律
复杂度O(n^3)据说有O(n^2.7)的写法