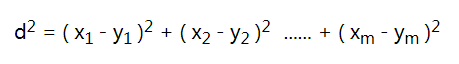机器学习（十）-KNN算法及Python实现

原创不易，转载前请注明博主的链接地址：Blessy_Zhu https://blog.csdn.net/weixin_42555080
本次代码的环境：
运行平台： Windows
Python版本： Python3.x
IDE： PyCharm
　

　

一、kNN算法简介

KNN算法是一个理论上比较成熟的方法,最初由Cover和Hart于1968年提出,其思路非常简单直观,易于快速实现,以及错误低的优点。k-近邻算法（kNN，k-NearestNeighbor），是最简单的机器学习分类算法之一，其核心思想在于用距离目标最近的k个样本数据的分类来代表目标的分类（这k个样本数据和目标数据最为相似）。
具体讲，存在训练样本集， 每个样本都包含数据特征和所属分类值。输入新的数据，将该数据和训练样本集汇中每一个样本比较，找到距离最近的k个，在k个数据中，出现次数做多的那个分类，即可作为新数据的分类。
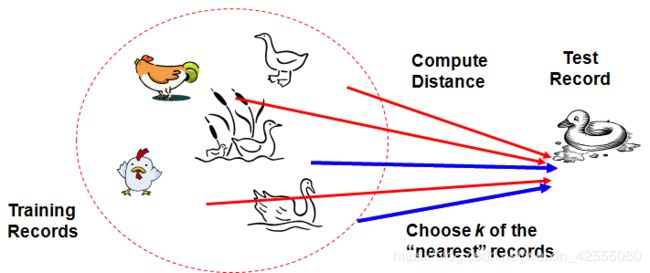
如下图所示：

　

利用KNN的思想：如果走像鸭子，叫像鸭子，看起来还像鸭子，那么它可能就是鸭子

二、kNN算法理解

2.1 算法理解

算法流程可以理解为：

1. 准备数据，对数据进行预处理
2. 选用合适的数据结构存储训练数据和测试元组
3. 设定参数，如k
4. 维护一个大小为k的的按距离由大到小的优先级队列，用于存储最近邻训练元组。随机从训练元组中选取k个元组作为初始的最近邻元组，分别计算测试元组到这k个元组的距离，将训练元组标号和距离存入优先级队列
5. 遍历训练元组集，计算当前训练元组与测试元组的距离，将所得距离L 与优先级队列中的最大距离Lmax
6. 进行比较。若L>=Lmax，则舍弃该元组，遍历下一个元组。若L < Lmax，删除优先级队列中最大距离的元组，将当前训练元组存入优先级队列。
7. 遍历完毕，计算优先级队列中k 个元组的多数类，并将其作为测试元组的类别。
8. 测试元组集测试完毕后计算误差率，继续设定不同的k值重新进行训练，最后取误差率最小的k 值。

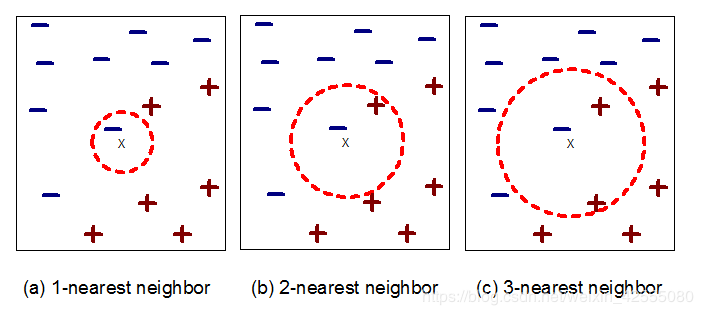
通过KNN的算法过程，要理解KNN一定要看这张最经典解释KNN的图：
　

　

如上图需要判断绿色是什么形状?当k等于3时，属于三角。当k等于5是，属于方形。

因此该方法具有一下特点：

• 监督学习：训练样本集中含有分类信息
• 算法简单， 易于理解实现
• 结果收到k值的影响，k一般不超过20.
• 计算量大，需要计算与样本集中每个样本的距离。
• 训练样本集不平衡导致结果不准确问题
  
  既然是监督学习，接下来，KNN算法实现就被分为两部分：
• 训练样本
  • 存放记录的集合
  • 用于计算记录间距离的距离度量
  • 检索最近邻的个数k
• 对一个未分类的记录进行分类:
  • 计算该记录与训练记录的距离
  • 计算出 k 个最近邻集合
  • 使用最近邻的类标号标记该记录的类标号（或进行投票）

2.2 分类决策规则

既然KNN是选择k个临近进行投票表决，那么他的决策规则有哪些呢？k近邻法(KNN)中得分类决策规则，常用多数表决法，当然，为了弱化k值的影响，还可以采用加权表决法。

• 多数表决
  由输入实例的k个邻近的训练实例中的多数类决定输入实例的类
  不考虑距离加权影响，每个投票权重都为1
• 加权表决
  由输入实例的k个邻近的训练实例中的多数类加权决定输入实例的类
  即根据距离的远近，对近邻的投票进行加权，距离越近则权重越大（权重为距离平方的倒数）
  为什么要使用多数表决法呢，这里给出多数表决法的直观解释？
  

三 KNN算法的缺点及改进

KNN算法是惰性学习法,学习程序直到对给定的测试集分类前的最后一刻对构造模型。在分类时,这种学习法的计算开销在和需要大的存储开销。总结KNN方法不足之处主要有下几点:①分类速度慢。②属性等同权重影响了准确率。③样本库容量依懒性较强。④K值的确定。

3.1 分类速度慢

从降低计算复杂度提高算法的执行效率。KNN算法存储训练集的所有样本数据,这造成了极大的存储开销和计算代价。已经提出了很多减少计算的算法,这些算法大致可分为两类。第一类,减少训练集的大小。KNN算法存储的样本数据,这些样本数据包含了大量冗余数据,这些冗余的数据增了存储的开销和计算代价。缩小训练样本的方法有:在原有的样本中删掉一部分与分类相关不大的样本样本,将剩下的样本作为新的训练样本;或在原来的训练样本集中选取一些代表样本作为新的训练样本;或通过聚类,将聚类所产生的中心点作为新的训练样本。这些方法筛选合适的新训练样本,对于大训练样本集,这个工作量是非常巨大的。第二类,采用快速算法,快速搜索到K个最近邻。KNN算法要找到K个最近邻的点,则要计算测试点到所有训练样本的距离,然后找出其中K个距离最小有数据点,当训练样本非常大时,KNN算法就不切实际了,为了加快KNN搜索过程,主要的方法,其中一个方法是部分距离计算如基于小波域部分距离计算的KNN搜 索 算 法 、快 速 算 法(KWENNS)。另外一种方法是,引入高效的索引方法,高效的索引方法可以大大降低K个最近邻的计算开销,特别是在高维空间中体现更为明显,比如现在研究提出一种新的索引结存模型,有的算法虽然能够有效降低K个最近邻的计算开销,提高了KNN的分类速度,但它们无法保证进行全局的最优搜索。

3.2 属性等同权重影响了准确率

采用优化相似度度量方法。基本的KNN算法基于欧基里德距离来计算相似度,这种计算距离的度量标准造成了KNN算法对噪声特征非常敏感。为了改变传统KNN算法中特征作用相同的缺陷,可在度量相似度的距离公式中给特征赋予不同权重,特征的权重一般根据各个特征在分类中的作用设定。可根据特征在整个训练样本库中的分类作用得到权重,也可根据其在训练样本的局部样本(靠近待测试样本的样本集合)中的分类作用得到权重。人们研究了各 种 学 习 调 整 权 值 的 方 法 ,从 而 提 高 了KNN分类器的性能。

3.3 样本库容量依懒性较强

采用优化判决策略。传统KNN的决策规则一个明显的缺点是,当样本分布密度不均匀时,只按照前K个近邻顺序而不考虑它们的距离会造成误判,影响分类的性能。而且在实际设计分类器时,由于一些类别比另一些类别的训练样本更容易获得,往往会造成训练样本各类别之间目数不均衡,即是训练样本在各个类中的数目基本接近,由于其所占区域大小的不同,也会造成训练样本的分布不均匀。目前改进的方法有均匀化样本分布密度;相关研究对kNN的决策规则进行了改进,很好地解决了当各类数据分布不均匀时kNN分类器分类性
能下降的问题,还有一些相关研究利用大量近邻集来代替KNN中的单一集合,并通过累加近邻的数据集对不同类别的支持度,获得相对可信的支持值,从而改善了近邻判决规则。

3.4 K值的确定

选取恰当的K值。由于KNN算法中几乎所有的计算都发生在分类阶段,而且分类效果很大程度上依赖于k值的选取,k值的选择很重要。k值选择过小,得到的近邻数过少,会降低分类精度,同时也会放大噪声数据的干扰;而如果k值选择过大,并且待分类样本属于训练集中包含数据数较少的类,那么在选择k个近邻的时候,实际上并不相似的数据亦被包含进来,造成噪声增加而导致分类效果的降低。如何选取恰当的K值也成为KNN的研究热点。

3.5 多种算法集成

除了上述的各种方法外,也有研究者将KNN分类方法和其他算法进行集成从而提高KNN分类器的分类性能。有将SVM和KNN进行集成,将KNN、Grouping和LSA进行集成,将遗传算法和模糊KNN进行集成,将贝叶斯分类器和KNN分类器进行集成,将P-tree和KNN相结合,通过和其他算法集成从而提高了KNN分类器的分类性能。

四 KNN算法的Python实现

既然是k近邻，那怎么定义这两者之间的“距离”呢？
这里采用

• 在二维空间中，有：
  
• 在三维空间中，两点的距离被定义为：
  
  我们可以据此推广到m维空间中，定义m维空间的距离：
  

要实现kNN算法，我们只需要计算出每一个样本点与测试点的距离，选取距离最近的k个样本，获取他们的标签（label) ，然后找出k个样本中数量最多的标签，返回该标签。
开始写之前还需要重视到标准化的重要性，举个栗子：
要分辨一个人的性别，一个女生的身高是1.70m，体重是60kg，一个男生的身高是1.80m，体重是70kg，而一个未知性别的人的身高是1.81m, 体重是64kg，这个人与女生数据点的“距离”的平方 d2 = ( 1.70 - 1.81 )2 + ( 60 - 64 )2 = 0.0121 + 16.0 = 16.0121，而与男生数据点的“距离”的平方d2 = ( 1.80 - 1.81 )2 + ( 70 - 64 )2 = 0.0001 + 36.0 = 36.0001 。可见，在这种情况下，身高差的平方相对于体重差的平方基本可以忽略不计，但是身高对于辨别性别来说是十分重要的。为了解决这个问题，就需要将数据标准化（normalize），把每一个特征值除以该特征的范围，保证标准化后每一个特征值都在0~1之间。
这样首先就要写一个normData函数来执行标准化数据集的工作：

def standard(dataSet):
    maxVals = dataSet.max(axis=0)
    minVals = dataSet.min(axis=0)
    ranges = maxVals - minVals
    retData = (dataSet - minVals) / ranges
    return retData, ranges, minVals

然后开始实现kNN算法：

def kNN(dataSet, labels, testData, k):
    distSquareMat = (dataSet - testData) ** 2 # 计算差值的平方
    distSquareSums = distSquareMat.sum(axis=1) # 求每一行的差值平方和
    distances = distSquareSums ** 0.5 # 开根号，得出每个样本到测试点的距离
    sortedIndices = distances.argsort() # 排序，得到排序后的下标
    indices = sortedIndices[:k] # 取最小的k个
    labelCount = {} # 存储每个label的出现次数
    for i in indices:
        label = labels[i]
        labelCount[label] = labelCount.get(label, 0) + 1 # 次数加一
    sortedCount = sorted(labelCount.items(), key=opt.itemgetter(1), reverse=True) 
    # 对label出现的次数从大到小进行排序
    return sortedCount[0][0] # 返回出现次数最大的label

接下来用几个小数据验证一下kNN函数是否能正常工作：

if __name__ == "__main__":
    dataSet = np.array([[2, 3], [3, 3],[6, 8],[7, 8]])
    normDataSet, ranges, minVals = normData(dataSet)
    labels = ['a', 'b','a', 'b']
    testData = np.array([3.9, 5.5])
    normTestData = (testData - minVals) / ranges
    result = kNN(normDataSet, labels, normTestData, 1)
    print(result)

输出结果：

a

五 总结

KNN算法是一个性能优秀的分类算法,人们正在从不同角度提出改进KNN算法,推动了KNN算法的研究工作,使KNN算法的研究得到了快速的发展。本篇文章介绍的是KNN算法。k-NN的特点:

• (1)是一种基于实例的学习
• (2)需要一个邻近性度量来确定实例间的相似性或距离
• (3)不需要建立模型，但分类一个测试样例开销很大
• (4)基于局部信息进行预测，对噪声非常敏感
• (5)最近邻分类器可以生成任意形状的决策边界
  • 决策树和基于规则的分类器通常是直线决策边界
• (6)需要适当的邻近性度量和数据预处理
  • 防止邻近性度量被某个属性左右

这篇文章就到这里了，欢迎大佬们多批评指正，也欢迎大家积极评论多多交流。
　

　

附完整代码

def standard(dataSet):
    maxVals = dataSet.max(axis=0)
    minVals = dataSet.min(axis=0)
    ranges = maxVals - minVals
    retData = (dataSet - minVals) / ranges
    return retData, ranges, minVals
def kNN(dataSet, labels, testData, k):
    distSquareMat = (dataSet - testData) ** 2 # 计算差值的平方
    distSquareSums = distSquareMat.sum(axis=1) # 求每一行的差值平方和
    distances = distSquareSums ** 0.5 # 开根号，得出每个样本到测试点的距离
    sortedIndices = distances.argsort() # 排序，得到排序后的下标
    indices = sortedIndices[:k] # 取最小的k个
    labelCount = {} # 存储每个label的出现次数
    for i in indices:
        label = labels[i]
        labelCount[label] = labelCount.get(label, 0) + 1 # 次数加一
    sortedCount = sorted(labelCount.items(), key=opt.itemgetter(1), reverse=True) 
    # 对label出现的次数从大到小进行排序
    return sortedCount[0][0] # 返回出现次数最大的label
 if __name__ == "__main__":
    dataSet = np.array([[2, 3], [3, 3],[6, 8],[7, 8]])
    normDataSet, ranges, minVals = normData(dataSet)
    labels = ['a', 'b','a', 'b']
    testData = np.array([3.9, 5.5])
    normTestData = (testData - minVals) / ranges
    result = kNN(normDataSet, labels, normTestData, 1)
    print(result)

参考文章

1 引入sklearn包中的knn类KNeighborsClassifier的使用
2 KNN分类决策规则
3 机器学习模型1 K-Nearest Neighbor（KNN）算法-基于Python sklearn的实现
4 机器学习之kNN算法(纯python实现：约会网站配对)
5 论文：KNN算法综述
6 利用Python实现kNN算法