算法竞赛专题解析(11):DP概述和常见DP面试题
本系列文章将于2021年整理出版,书名《算法竞赛专题解析》。
前驱教材:《算法竞赛入门到进阶》 清华大学出版社
网购:京东 当当 作者签名书
如有建议,请加QQ 群:567554289,或联系作者QQ:15512356
文章目录
- 1 DP概述
- 1.1 DP问题的特征
- 1.2 DP的两种实现
- 2 经典DP面试问题
- 2.1 0/1背包问题(0/1 Knapsack Problem)
- 2.2 最长公共子序列(Longest Common Subsequence,LCS)
- 2.3 最长上升子序列(Longest Increasing Subsequence,LIS)
- 2.4 编辑距离(Edit Distance)
- 2.5 最小划分(Minimum Partition)
- 2.6 行走问题(Ways to Cover a Distance)
- 2.7 矩阵最长递增路径(Longest Path In Matrix)
- 2.8 子集和问题 (Subset Sum Problem)
- 2.9 最优游戏策略(Optimal Strategy for a Game)
- 2.10 矩阵链乘法(Matrix Chain Multiplication)
动态规划(DP)是一种算法技术,它将大问题分解为更简单的子问题,对整体问题的最优解决方案取决于子问题的最优解决方案。
1 DP概述
1.1 DP问题的特征
下面以斐波那契数为例说明DP的概念。斐波那契数列的每个数字是前面两个数字的和,前几个数是1、1、2、3、5、8。计算第n个斐波那契数,用递推公式进行计算:
f i b ( n ) = f i b ( n − 1 ) + f i b ( n − 2 ) fib(n) = fib(n-1) + fib(n-2) fib(n)=fib(n−1)+fib(n−2)
用递归编程,代码如下。
int fib (int n){
if (n == 1 || n == 2)
return 1;
return (fib (n -1) + fib (n -2));
}
为了解决总体问题 f i b ( n ) fib(n) fib(n),将其分解为两个较小的子问题 f i b ( n − 1 ) fib(n-1) fib(n−1)和 f i b ( n − 2 ) fib(n-2) fib(n−2)。这就是DP的应用场景。
有一些问题有2个特征:重叠子问题、最优子结构。用DP可以高效率地处理具有这2个特征的问题。
(1)重叠子问题
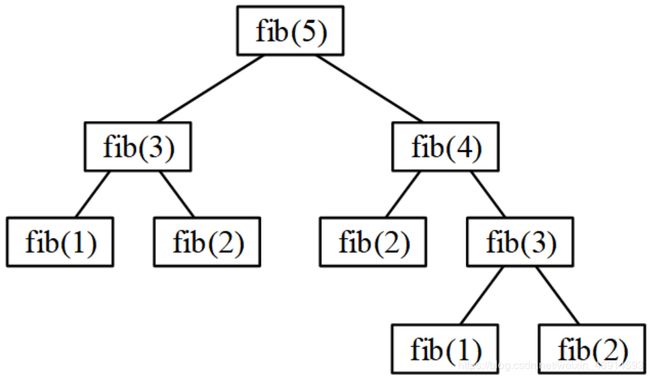
首先,子问题是原大问题的小版本,计算步骤完全一样;其次,计算大问题的时候,需要多次重复计算小问题。这就是“重叠子问题”。以斐波那契数为例,用递归计算 f i b ( 5 ) fib(5) fib(5),分解为以下子问题:
其中 f i b ( 3 ) fib(3) fib(3)计算了2次,其实只算1次就够了。
一个子问题的多次计算,耗费了大量时间。用DP处理重叠子问题,每个子问题只需要计算一次,从而避免了重复计算,这就是DP效率高的原因。具体的做法是:首先分析得到最优子结构,然后用递推或者记忆化递归进行编程,从而实现了高效的计算。
需要注意的是,DP在获得时间高效率的同时,可能耗费更多的空间,即“时间效率高,空间耗费大”。滚动数组是优化空间效率的一个办法。
(2)最优子结构
最优子结构的意思是:首先,大问题的最优解包含小问题的最优解;其次,可以通过小问题的最优解推导出大问题的最优解。在斐波那契问题中,把数列的计算构造成 f i b ( n ) = f i b ( n − 1 ) + f i b ( n − 2 ) fib(n) = fib(n-1) + fib(n-2) fib(n)=fib(n−1)+fib(n−2),即把原来为 n n n的大问题,减小为 n − 1 n-1 n−1和 n − 2 n-2 n−2的小问题,这是斐波那契数的最优子结构。
在DP的概念中,还常常提到“无后效性”,简单地说就是“未来与过去无关”、“过去不影响未来”。此概念不太容易理解,下面以走楼梯问题为例进行解释。
走楼梯问题:一次可以走一个台阶或者两个台阶,问走到第n个台阶时,一共有多少种走法?
它的数学模型就是斐波那契数列 f i b ( n ) = f i b ( n − 1 ) + f i b ( n − 2 ) fib(n) = fib(n-1) + fib(n-2) fib(n)=fib(n−1)+fib(n−2)。要走到第 n n n级台阶,有两种方法,一种是从 n − 1 n-1 n−1级台阶走一步过来,一种是从 n − 2 n-2 n−2级台阶走两步过来。但是,前面是怎么走到第 n − 1 n-1 n−1级,怎么走到 n − 2 n-2 n−2级台阶, f i b ( n − 1 ) fib(n-1) fib(n−1)和 f i b ( n − 2 ) fib(n-2) fib(n−2)是如何计算得到的,并不需要知道,只需要它们的计算结果就行了。换句话说,“只关心前面的结果,不关心前面的过程”,在计算 f i b ( n ) fib(n) fib(n)的时候,只需要 f i b ( n ) fib(n) fib(n)和 f i b ( n − 1 ) fib(n-1) fib(n−1)的结果,不需要知道它们的计算过程,这就是无后效性。
无后效性是应用DP的必要条件,因为只有这样,才能减少算法的复杂度,应用DP才有意义。如果不满足无后效性,那么在计算 f i b ( n ) fib(n) fib(n)的时候,还需要重新计算 f i b ( n − 1 ) fib(n-1) fib(n−1)、 f i b ( n − 2 ) fib(n-2) fib(n−2),算法并没有优化。
从最优子结构的概念可以看出,它是满足无后效性的。
这里用斐波那契数列举例说明DP的概念,可能过于简单,不足以说明DP的特征。建议读者用后文的经典问题“0/1背包”,重新理解DP的特征。
1.2 DP的两种实现
处理DP中的大问题和小问题,有两种思路:自顶向下(先大问题再小问题)、自下而上(先小问题再大问题)。
编码实现DP时,自顶向下用带记忆化的递归,自下而上用递推。两种方法的复杂度是一样的,每个子问题都计算一遍,而且只计算一遍。
(1)自顶向下与记忆化递归
先考虑大问题,再缩小到小问题,递归很直接地体现了这种思路。为避免递归时重复计算子问题,可以在子问题得到解决时,就保存结果,再次需要这个结果时,直接返回保存的结果就行了。这种存储已经解决的子问题的结果的技术称为“记忆化(Memoization)”。
以斐波那契数为例,记忆化代码如下:
int memoize[maxn]; //保存结果
int fib (int n){
if (n == 1 || n == 2)
return 1;
if(memoize[n] != 0) //直接返回保存的结果,不再递归
return memoize[n];
memoize[n]= fib (n - 1) + fib (n - 2); //递归计算结果,并记忆
return memoize[n];
}
(2)自下而上与制表递推
这种方法与递归的自顶向下相反,避免了递归的编程方法。这种“自下而上”的方法,先解决子问题,再递推到大问题。通常通过填写多维表格来完成。根据表中的结果,逐步计算出大问题的解决方案。
用制表法计算斐波那契数,维护一个一维表 d p [ ] dp[] dp[],记录自下而上的计算结果,更大的数是前面两个数的和。
代码如下:
const int maxn = 255;
int dp[maxn];
int fib (int n){
dp[1] = dp[2] =1;
for (int i = 3;i<=n;i++)
dp[i] = dp[i-1] +dp[i-2];
return dp[n];
}
在DP编程时,大多使用制表递推的编程方法。超过4维( d p [ ] [ ] [ ] [ ] dp[][][][] dp[][][][])的表格也是常见的。
2 经典DP面试问题
本节介绍了10个经典的DP面试问题1,并且以第一个“0/1背包问题”为例,详细解释与DP有关的内容:
(1)dp的设计;
(2)dp方程的推导;
(3)记忆化和递推编码;
(4)具体方案的输出;
(5)滚动数组。DP使用的空间可以用滚动数组优化。DP的状态方程,常常是二维和二维以上,占用了太多的空间。滚动数组是减少空间的技术,例如它可以把二维状态方程的 O ( n 2 ) O(n^2) O(n2)空间复杂度,优化到 O ( n ) O(n) O(n),更高维的数组也可以优化。
2.1 0/1背包问题(0/1 Knapsack Problem)
问题描述:给定 n n n种物品和一个背包,物品 i i i的重量是 w i w_i wi,价值为 v i v_i vi,背包的总容量为 C C C。把物品装入背包时,第 i i i种物品只有两种选择:装入背包或不装入背包,称为0/1背包。如何选择装入背包的物品,使得装入背包中的物品的总价值最大?
设 x i x_i xi表示物品 i i i装入背包的情况: x i = 0 x_i=0 xi=0时,不装入背包; x i = 1 x_i=1 xi=1时,装入背包。有以下约束条件和目标函数:
约束条件: ∑ i = 1 n w i x i ≤ C \sum_{i=1}^nw_ix_i \leq C ∑i=1nwixi≤C x i ∈ { 0 , 1 } , 1 ≤ i ≤ n x_i\in\{0,1\},1 \leq i \leq n xi∈{0,1},1≤i≤n
目标函数: m a x ∑ i = 1 n v i x i max \sum_{i=1}^nv_ix_i max∑i=1nvixi
下面以0/1背包问题为例,详细解释DP相关知识点。首先看一个例题。
hdu 2602 Bone Collector http://acm.hdu.edu.cn/showproblem.php?pid=2602
问题描述:“骨头收集者”带着体积C的背包去捡骨头,已知每个骨头的体积和价值,求能装进背包的最大价值。N <= 1000,C<= 1000。
输入:第1行是测试数量;后面每3行是1个测试,其中第1行是骨头数量N和背包体积C,第2行是每个骨头的价值,第3行是每个骨头的体积。
输出:
最大价值。
样例输入:
1
5 10
1 2 3 4 5
5 4 3 2 1
样例输出:
14
(1)dp的设计
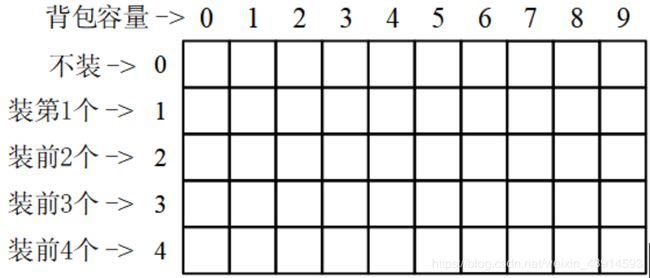
引进一个 ( N + 1 ) × ( C + 1 ) (N+1)×(C+1) (N+1)×(C+1)大小的二维数组 d p dp dp, d p [ i ] [ j ] dp[i][j] dp[i][j]表示把前 i i i个物品(从第1个到第 i i i个)装入容量为 j j j的背包中获得的最大价值。
可以把每个 d p [ i ] [ j ] dp[i][j] dp[i][j]都看成一个背包,最后的 d p [ N ] [ C ] dp[N][C] dp[N][C]就是答案:把 N N N个物品装进容量 C C C的背包。
(2)dp转移方程
现在自下而上计算dp,假设现在递推到 d p [ i ] [ j ] dp[i][j] dp[i][j],它表示把前 i i i个物品装进容量为 j j j的背包。分2种情况:
1)第 i i i个物品的体积比容量 j j j还大,不能装进容量 j j j的背包。那么直接继承前 i − 1 i-1 i−1个物品装进容量 j j j的背包的情况即可: d p [ i ] [ j ] = d p [ i − 1 ] [ j ] dp[i][j] = dp[i-1][j] dp[i][j]=dp[i−1][j]。
2)第 i i i个物品的体积比容量 j j j小,能装进背包。又可以分为2种情况:装或者不装第 i i i个。
(a)装第 i i i个。从前 i − 1 i-1 i−1个物品的情况下推广而来,前 i − 1 i-1 i−1个物品是 d p [ i − 1 ] [ j ] dp[i-1][j] dp[i−1][j]。第 i i i个物品装进背包后,背包容量减少 b o n e [ i ] . v o l u m bone[i].volum bone[i].volum,价值增加 b o n e [ i ] . v a l u e bone[i].value bone[i].value。所以有:
d p [ i ] [ j ] = d p [ i − 1 ] [ j − b o n e [ i ] . v o l u m ] + b o n e [ i ] . v a l u e dp[i][j] = dp[i-1][j-bone[i].volum] + bone[i].value dp[i][j]=dp[i−1][j−bone[i].volum]+bone[i].value
(b)不装第 i i i个。那么: d p [ i ] [ j ] = d p [ i − 1 ] [ j ] dp[i][j] = dp[i-1][j] dp[i][j]=dp[i−1][j]。
取(a)和(b)的最大值,状态转移方程是:
d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − b o n e [ i ] . v o l u m ] + b o n e [ i ] . v a l u e ) dp[i][j] = max(dp[i-1][j], dp[i-1][j-bone[i].volum] + bone[i].value) dp[i][j]=max(dp[i−1][j],dp[i−1][j−bone[i].volum]+bone[i].value)
总结上述分析,0/1背包问题的重叠子问题是 d p [ i ] [ j ] dp[i][j] dp[i][j],最优子结构是 d p [ i ] [ j ] dp[i][j] dp[i][j]的状态转移方程。
算法的时间复杂度:算法需要计算二维矩阵dp,二维矩阵大小是 N × C N×C N×C,每一项计算时间是 O ( 1 ) O(1) O(1),总复杂度是 O ( N × C ) O(N×C) O(N×C)。算法的空间复杂度是 O ( N × C ) O(N×C) O(N×C)。
0/1背包问题的简化版。一般物品有体积(或者重量)、价值这2个属性,求满足体积约束条件下的最大价值。如果再简单一点,只有一个体积属性,求能放到背包的最多物品,那么,只要把体积看成价值,求最大体积就好了。状态方程变为:
d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − v o l u m [ i ] ] + v o l u m [ i ] ) dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - volum[i]] + volum[i]) dp[i][j]=max(dp[i−1][j],dp[i−1][j−volum[i]]+volum[i])
(3)详解dp的转移过程
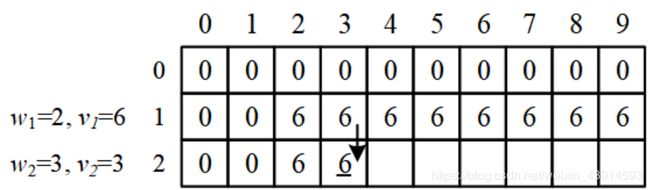
初学者可能对上面的描述仍不太清楚,下面用一个例子详细说明:有4个物品,其体积分别是{2, 3, 6, 5},价值分别为{6, 3, 5, 4},背包的容量为9。
填dp表的过程,按照只装第1个物品、只放前2个、只放前3个…的顺序,一直到装完,这就是从小问题扩展到大问题的过程。
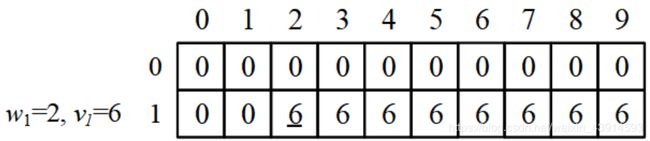
步骤1:只装第1个物品。
由于物品1的体积是2,所以背包容量小于2的,都放不进去,得 d p [ 1 ] [ 0 ] = d p [ 1 ] [ 1 ] = 0 dp[1][0]=dp[1][1]=0 dp[1][0]=dp[1][1]=0;
物品1的体积等于背包容量,能装进去,背包价值等于物品1的价值, d p [ 1 ] [ 2 ] = 6 dp[1][2]=6 dp[1][2]=6;
容量大于2的背包,多余的容量用不到,所以价值和容量2的背包一样。
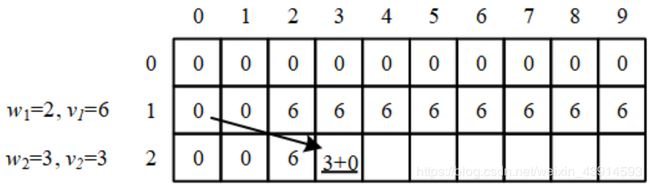
步骤2:只装前2个物品。
如果物品2体积比背包容量大,那么不能装物品2,情况和只装第1个一样。见下图中的 d p [ 2 ] [ 0 ] = d p [ 2 ] [ 1 ] = 0 , d p [ 2 ] [ 2 ] = 6 dp[2][0]=dp[2][1]=0,dp[2][2]=6 dp[2][0]=dp[2][1]=0,dp[2][2]=6。
下面填 d p [ 2 ] [ 3 ] dp[2][3] dp[2][3]。物品2体积等于背包容量,那么可以装物品2,也可以不装:
(a)如果装物品2(体积是3),那么可以变成一个更小的问题,即只把物品1装到(容量 - 3)的背包中。
取(a)和(b)的最大值,得 d p [ 2 ] [ 3 ] = m a x { 3 , 6 } = 6 dp[2][3] = max\{3,6\} = 6 dp[2][3]=max{3,6}=6。
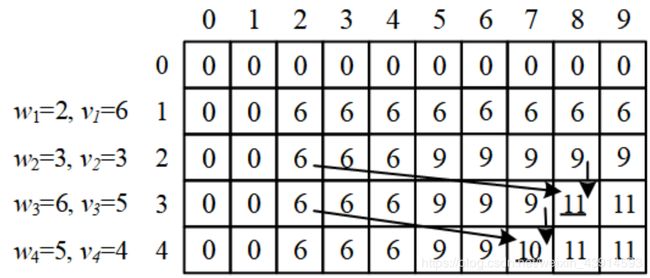
后续步骤:继续以上过程,最后得到下图(图中的箭头是几个例子):
最后的答案是 d p [ 4 ] [ 9 ] dp[4][9] dp[4][9]:把4个物品装到容量为9的背包,最大价值是11。
(4)输出背包方案
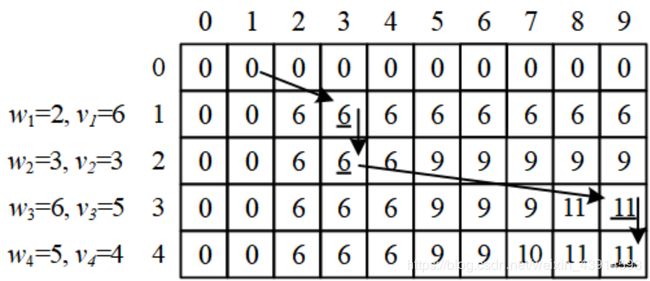
现在回头看具体装了哪些物品。需要倒过来观察:
d p [ 4 ] [ 9 ] = m a x d p [ 3 ] [ 4 ] + 4 , d p [ 3 ] [ 9 ] = d p [ 3 ] [ 9 ] dp[4][9]=max{dp[3][4]+4,dp[3][9]} = dp[3][9] dp[4][9]=maxdp[3][4]+4,dp[3][9]=dp[3][9],说明没有装物品4,用 x 4 = 0 x_4=0 x4=0表示;
d p [ 3 ] [ 9 ] = m a x d p [ 2 ] [ 3 ] + 5 , d p [ 2 ] [ 9 ] = d p [ 2 ] [ 3 ] + 5 = 11 dp[3][9]=max{dp[2][3]+5,dp[2][9]} = dp[2][3]+5 = 11 dp[3][9]=maxdp[2][3]+5,dp[2][9]=dp[2][3]+5=11,说明装了物品3, x 3 = 1 x_3=1 x3=1;
d p [ 2 ] [ 3 ] = m a x d p [ 1 ] [ 0 ] + 3 , d p [ 1 ] [ 3 ] = d p [ 1 ] [ 3 ] dp[2][3]=max{dp[1][0]+3,dp[1][3]} = dp[1][3] dp[2][3]=maxdp[1][0]+3,dp[1][3]=dp[1][3],说明没有装物品2, x 2 = 0 x_2=0 x2=0;
d p [ 1 ] [ 3 ] = m a x d p [ 0 ] [ 1 ] + 6 , d p [ 0 ] [ 3 ] = d p [ 0 ] [ 1 ] + 6 = 6 dp[1][3]=max{dp[0][1]+6,dp[0][3]} = dp[0][1]+6 = 6 dp[1][3]=maxdp[0][1]+6,dp[0][3]=dp[0][1]+6=6,说明装了物品1, x 1 = 1 x_1=1 x1=1。
图中的实线箭头指出了方案的路径。
(5)记忆化代码和递推代码
下面的代码分别用自下而上的递推和自上而下的记忆化递归实现。
1)递推代码。
#include2)记忆化代码。只改动了上面代码中的solve()。
int solve(int i, int j){ //前i个物品,放进容量j的背包
if (dp[i][j] != 0) //记忆化
return dp[i][j];
if(i == 0) return 0;
int res;
if(bone[i].volum > j) //第i个物品比背包还大,装不了
res = solve(i-1,j);
else //第i个物品可以装
res = max(solve(i-1,j), solve(i-1,j-bone[i].volum)+bone[i].value);
return dp[i][j] = res;
}
(6)滚动数组
上述代码使用了二维矩阵 d p [ ] [ ] dp[][] dp[][],有可能超过题目许可的空间限制。此时可以用滚动数组减少空间,也就是把 d p [ ] [ ] dp[][] dp[][]替换成一维的 d p [ ] dp[] dp[]。观察二维表 d p [ ] [ ] dp[][] dp[][],可以发现,每一行是从上面一行算出来的,只跟上面一行有关系,跟更前面的行没有关系,那么用新的一行覆盖原来的一行(滚动)就好了。
int dp[1011]; //替换 int dp[1011][1011];
int solve(int n, int c){
for(int i=1; i<=n; i++)
for(int j=c; j>=bone[i].volum; j--) //反过来循环
dp[j] = max(dp[j],dp[j-bone[i].volum]+bone[i].value);
return dp[c];
}
注意j应该反过来循环,即从后面往前面覆盖。请读者思考原因。
经过滚动数组的优化,空间复杂度从 O ( N × C ) O(N×C) O(N×C)减少为 O ( C ) O(C) O(C)。
滚动数组也有缺点。它覆盖了中间转移状态,只留下了最后的状态,所以损失了很多信息,导致无法输出背包的方案。
二维以上的dp数组也常常能优化。比如求 d p [ t ] [ ] [ ] dp[t][][] dp[t][][],如果它只和 d p [ t − 1 ] [ ] [ ] dp[t-1][][] dp[t−1][][]有关,不需 d p [ t − 2 ] [ ] [ ] dp[t-2][][] dp[t−2][][]、 d p [ t − 3 ] [ ] [ ] dp[t-3][][] dp[t−3][][]等,那么可以把数组缩小为 d p [ 2 ] [ ] [ ] dp[2][][] dp[2][][]。后面的很多问题都可以用滚动数组优化。
2.2 最长公共子序列(Longest Common Subsequence,LCS)
一个给定序列的子序列,是在该序列中删去若干元素后得到的序列。例如:X = { A , B , C , B , D , A , B A, B, C, B, D, A, B A,B,C,B,D,A,B},它的子序列有{ A , B , C , B , A A, B, C, B, A A,B,C,B,A}、{ A , B , D A, B, D A,B,D}、{ B , C , D , B B, C, D, B B,C,D,B}等。子序列和子串是不同的概念,子串的元素在原序列中是连续的。
给定两个序列 X X X和 Y Y Y,当另一序列 Z Z Z既是 X X X的子序列又是 Y Y Y的子序列时,称 Z Z Z是序列 X X X和 Y Y Y的公共子序列。最长公共子序列是长度最长的子序列。
问题描述:给定两个序列 X X X和 Y Y Y,找出 X X X和 Y Y Y的一个最长公共子序列。
用暴力法找最长公共子序列,需要先找出 X X X的所有子序列,然后验证是否 Y Y Y的子序列。如果 X X X有 m m m个元素,那么 X X X有 2 m 2^m 2m个子序列; Y Y Y有 n n n个元素;总复杂度大于 O ( n 2 m ) O(n2^m) O(n2m)。
用动态规划求LCS,复杂度是 O ( n m ) O(nm) O(nm)。
用 d p [ i ] [ j ] dp[i][j] dp[i][j]表示序列 X i X_i Xi(表示 x 1 , . . . , x i x_1,...,x_i x1,...,xi这个序列,即 X X X的前 i i i个元素组成的序列;这里用小写的 x x x表示元素,用大写的 X X X表示序列)和 Y j Y_j Yj(表示 y 1 , . . . , y j y_1,...,y_j y1,...,yj这个序列,即 Y Y Y的前 j j j个元素)的最长公共子序列的长度。 d p [ n ] [ m ] dp[n][m] dp[n][m]就是答案。
分解为2种情况:
(1)当 x i = y j x_i = y_j xi=yj时,找出 X i − 1 X_{i-1} Xi−1和 Y j − 1 Y_{j-1} Yj−1的最长公共子序列,然后在其尾部加上 x i x_i xi即可得到 X i X_i Xi 和 Y j Y_j Yj的最长公共子序列。
(2)当 x i ≠ y j x_i ≠ y_j xi=yj时,求解两个子问题: X i − 1 X_{i-1} Xi−1和 Y j Y_j Yj的最长公共子序列; X i X_i Xi和 Y j − 1 Y_{j-1} Yj−1的最长公共子序列。取其中的最大值。
状态转移方程是:
d p [ i ] [ j ] = d p [ i − 1 ] [ j − 1 ] + 1 dp[i][j] = dp[i-1][j-1] + 1 dp[i][j]=dp[i−1][j−1]+1 x i = y j x_i = y_j xi=yj
d p [ i ] [ j ] = m a x { d p [ i ] [ j − 1 ] , d p [ i − 1 ] [ j ] } dp[i][j] = max\{dp[i][j-1], dp[i-1][j]\} dp[i][j]=max{dp[i][j−1],dp[i−1][j]} x i ≠ y j x_i ≠ y_j xi=yj
习题:hdu 1159 Common Subsequence http://acm.hdu.edu.cn/showproblem.php?pid=1159
2.3 最长上升子序列(Longest Increasing Subsequence,LIS)
问题描述:给定一个长度为 n n n的数组,找出一个最长的单调递增子序列。
例如一个长度为6的序列 A = { 5 , 6 , 7 , 4 , 2 , 8 , 3 } A=\{5, 6, 7, 4, 2, 8, 3\} A={5,6,7,4,2,8,3},它最长的单调递增子序列为{ 5 , 6 , 7 , 8 5, 6, 7, 8 5,6,7,8},长度为4。
定义状态 d p [ i ] dp[i] dp[i],表示以第 i i i个数为结尾的最长递增子序列的长度,那么:
d p [ i ] = m a x { d p [ j ] } + 1 0 < j < i , A j < A i dp[i] = max\{dp[j]\}+1 \qquad 0< j < i, A_j < A_i dp[i]=max{dp[j]}+10<j<i,Aj<Ai
最后答案是 m a x { d p [ i ] } max\{dp[i]\} max{dp[i]}。
复杂度: j j j在 0 0 0 ~ i i i之间滑动,复杂度是 O ( n ) O(n) O(n); i i i的变动范围也是 O ( n ) O(n) O(n)的;总复杂度 O ( n 2 ) O(n^2) O(n2)。
DP并不是LIS问题的最优解法,有复杂度 O ( n l o g n ) O(nlogn) O(nlogn)的非DP解法[参考《算法竞赛入门到进阶》“7.1.4 最长递增子序列”的详细讲解。]。
习题:hdu 1257 最少拦截系统 http://acm.hdu.edu.cn/showproblem.php?pid=1257
2.4 编辑距离(Edit Distance)
问题描述:给定两个单词 w o r d 1 word1 word1和 w o r d 2 word2 word2,计算出将 w o r d 1 word1 word1转换为 w o r d 2 word2 word2所需的最小操作数。一个单词允许进行以下3种操作:(1)插入一个字符;(2)删除一个字符;(3)替换一个字符。
把长度为 m m m的 w o r d 1 word1 word1存储在数组 w o r d 1 [ 1 ] word1[1] word1[1] ~ w o r d 1 [ m ] word1[m] word1[m],长度为n的 w o r d 2 word2 word2存储在 w o r d 2 [ 1 ] word2[1] word2[1] ~ w o r d 2 [ n ] word2[n] word2[n]。不用 w o r d 1 [ 0 ] word1[0] word1[0]和 w o r d 2 [ 0 ] word2[0] word2[0]。
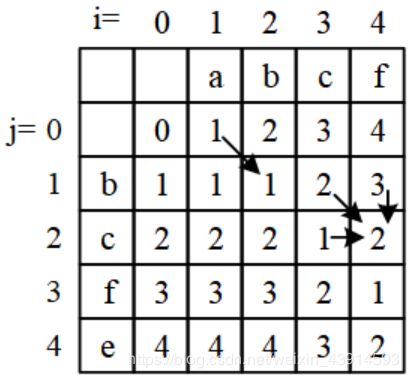
定义二维数组 d p dp dp, d p [ i ] [ j ] dp[i][j] dp[i][j]表示从 w o r d 1 word1 word1 的前 i i i个字符转换到 w o r d 2 word2 word2 的前j个字符所需要的操作步骤, d p [ m ] [ n ] dp[m][n] dp[m][n]就是答案。下图是 w o r d 1 = ” a b c f ” word1=”abcf” word1=”abcf”, w o r d 2 = ” b c f e ” word2=”bcfe” word2=”bcfe”的 d p dp dp转移矩阵。
状态转移方程:
(1)若 w o r d 1 [ i ] = w o r d 2 [ j ] word1[i] = word2[j] word1[i]=word2[j],则 d p [ i ] [ j ] = d p [ i − 1 ] [ j − 1 ] dp[i][j] = dp[i-1][j-1] dp[i][j]=dp[i−1][j−1]。例如图中 d p [ 2 ] [ 1 ] dp[2][1] dp[2][1]处的箭头。
(2)其他情况: d p [ i ] [ j ] = m i n { d p [ i − 1 ] [ j − 1 ] , d p [ i − 1 ] [ j ] , d p [ i ] [ j − 1 ] } + 1 dp[i][j] = min\{dp[i-1][j-1], dp[i-1][j], dp[i][j-1]\} + 1 dp[i][j]=min{dp[i−1][j−1],dp[i−1][j],dp[i][j−1]}+1。例如图中 d p [ 4 ] [ 2 ] dp[4][2] dp[4][2]处的箭头。 d p [ i ] [ j ] dp[i][j] dp[i][j]是它左、左上、上的三个值中的最小值加1,分别对应以下操作:
1) d p [ i − 1 ] [ j ] + 1 dp[i-1][j]+1 dp[i−1][j]+1,删除,将 w o r d 1 word1 word1的最后字符删除;
2) d p [ i ] [ j − 1 ] + 1 dp[i][j-1]+1 dp[i][j−1]+1,插入,在 w o r d 2 word2 word2的最后插入 w o r d 1 word1 word1的最后字符;
3) d p [ i − 1 ] [ j − 1 ] + 1 dp[i-1][j-1]+1 dp[i−1][j−1]+1,替换,将 w o r d 2 word2 word2的最后一个字符替换为 w o r d 1 word1 word1的最后一个字符。
复杂度: O ( m n ) O(mn) O(mn)。
习题:力扣72 编辑距离https://leetcode-cn.com/problems/edit-distance/
2.5 最小划分(Minimum Partition)
问题描述:给出一个正整数数组,把它分成S1、S2两部分,使S1的数字和与S2的数字和的差的绝对值最小。最小划分的特例是S1和S2的数字和相等,即差为0。
例如:数组 [ 1 , 6 , 11 , 5 ] [1, 6, 11, 5] [1,6,11,5],最小划分是 S 1 = [ 1 , 5 , 6 ] S1 = [1, 5, 6] S1=[1,5,6], S 2 = [ 11 ] S2 = [11] S2=[11]; S 1 S1 S1的数字和减去 S 2 S2 S2的数字和,绝对值是 ∣ 11 − 12 ∣ = 1 |11 - 12| = 1 ∣11−12∣=1。
最小划分问题可以转化为0/1背包问题。求出数组的和 s u m sum sum,把问题转化成:背包的容量为 s u m / 2 sum/2 sum/2,把数组的每个数字看成物品的体积,求出背包最多可以放 r e s res res体积的物品,返回结果 ∣ r e s − ( s u m − r e s ) ∣ |res-(sum-res)| ∣res−(sum−res)∣。
习题:lintcode 724 Minimum Partition
https://www.lintcode.com/problem/minimum-partition/description
2.6 行走问题(Ways to Cover a Distance)
问题描述:给定一个整数 n n n表示距离,一个人每次能走1、2、3步,问走到n步,有多少种走法。例如 n n n = 3,有4种走法:{1, 1, 1}、{1, 2}、{2, 1}、{3}。
和爬楼梯问题差不多。爬楼梯问题是每次能走1级或2级,问走到第n级有多少种走法。爬楼梯的解实际上是一个斐波那契数列。
定义行走问题的状态 d p [ i ] dp[i] dp[i]为走到第 i i i步的走法数量,那么有:
d p [ 0 ] = 1 , d p [ 1 ] = 1 , d p [ 2 ] = 2 dp[0] = 1,dp[1] = 1,dp[2] = 2 dp[0]=1,dp[1]=1,dp[2]=2
当i > 2时: d p [ i ] = d p [ i − 1 ] + d p [ i − 2 ] + d p [ i − 3 ] dp[i] = dp[i-1] + dp[i-2] + dp[i-3] dp[i]=dp[i−1]+dp[i−2]+dp[i−3]
2.7 矩阵最长递增路径(Longest Path In Matrix)
问题描述:给定一个矩阵,找一条最长路径,要求路径上的数字递增。矩阵的每个点,可以往上、下、左、右四个方向移动,不能沿对角线方向移动。
例如矩阵:
9 9 3 7 5 7 3 1 1 \begin{matrix} 9 & 9 & 3 \\ 7 & 5 & 7 \\ 3 & 1 & 1\end{matrix} 973951371
它的一个最长递增路径是[1, 3, 7, 9],长度是4。
下面给出2种解法:
(1)暴力DFS。设矩阵有m×n个点,以每个点为起点做DFS搜索递增路径,在所有递增路径中找出最长的路径。每个DFS都是指数时间复杂度的,复杂度非常高。
(2)记忆化搜索。在暴力DFS的基础上,用记忆化进行优化。把每个点用DFS得到的最长递增路径记下来,后面再搜到这个点时,直接返回结果。由于每个点只计算一次,每个边也只计算一次,虽然做了m×n次DFS搜索,但是总复杂度仍然是O(V+E)= O(mn)的,其中V是点数,E是边数。这也算是动态规划的方法。
习题: 力扣329 矩阵中的最长递增路径
https://leetcode-cn.com/problems/longest-increasing-path-in-a-matrix/
2.8 子集和问题 (Subset Sum Problem)
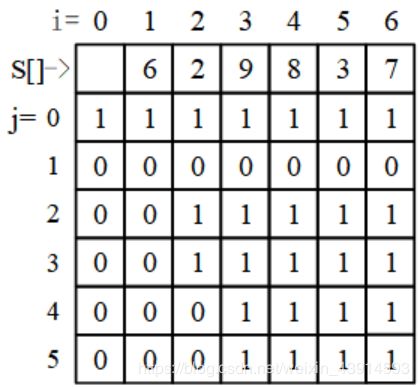
问题描述:给定一个非负整数的集合S,一个值M,问S中是否有一个子集,子集和等于M。
例如:S[] = {6, 2, 9, 8, 3, 7}, M = 5,存在一个子集{2, 3},子集和等于5。
用暴力法求解,即检查所有的子集。子集共有有 2 n 2^n 2n个,为什么?用二进制帮忙理解:一个元素被选中,标记为1;没有选中,标记为0;空集是n个0,所有元素都被选中是n个1,从n个0到n个1,共有 2 n 2^n 2n个。
用DP求解,定义二维数组 d p dp dp。当 d p [ i ] [ j ] dp[i][j] dp[i][j]等于1时,表示S的前 i i i个元素存在一个子集和等于 j j j。题目的答案就是dp[n][M]。
用S[1]~S[n]记录集合S的n个元素。
状态转移方程,分析如下:
(1)若S[i] > j,则S[i]不能放在子集中,有 d p [ i ] [ j ] = d p [ i − 1 ] [ j ] dp[i][j] = dp[i-1][j] dp[i][j]=dp[i−1][j];
(2)若S[i] <= j, 有两种选择:
不把S[i]放在子集中,则 d p [ i ] [ j ] = d p [ i − 1 ] [ j ] dp[i][j] = dp[i-1][j] dp[i][j]=dp[i−1][j];
把S[i]放在子集中,则 d p [ i ] [ j ] = d p [ i − 1 ] [ j − S [ i ] ] dp[i][j]= dp[i-1][j-S[i]] dp[i][j]=dp[i−1][j−S[i]]。
这2种选择,只要其中一个为1,那么 d p [ i ] [ j ] dp[i][j] dp[i][j]就为1。
读者可以用下面的图例进行验证。
如果已经确定问题有解,即 d p [ n ] [ M ] = 1 dp[n][M]=1 dp[n][M]=1,如何输出子集内的元素?按推导转移方程的思路,从 d p [ n ] [ M ] dp[n][M] dp[n][M]开始,沿着 d p dp dp矩阵倒推回去即可。
2.9 最优游戏策略(Optimal Strategy for a Game)
问题描述:有 n n n堆硬币排成一行,它们的价值分别是 v 1 , v 2 , . . . , v n v_1, v_2, ..., v_n v1,v2,...,vn, n n n为偶数;两人交替拿硬币,每次只能在剩下的硬币中,拿走第一堆或最后一堆硬币。如果你是先手,你能拿到的最大价值是多少?
例如:{8, 15, 3, 7},先手这样拿可以获胜:(1)先手拿7;(2)对手拿8;(3)先手拿15;(4)对手拿3,结束。先手拿到的最大价值是7 + 15 = 22。
这一题不能用贪心法。比如在样例中,如果先手第一次拿8,那么对手接下来肯定拿15,先手失败。
定义二维 d p dp dp, d p [ i ] [ j ] dp[i][j] dp[i][j]表示从第 i i i堆到 j j j堆硬币区间内,先手能拿到的最大值。
在硬币区间 [ i , j ] [i, j] [i,j],先手有两个选择:
1)拿 i i i。接着对手也有2个选择,拿 i + 1 i+1 i+1或 j j j:拿 i + 1 i+1 i+1,剩下 [ i + 2 , j ] [i+2, j] [i+2,j];拿 j j j,剩下 [ i + 1 , j − 1 ] [i+1, j-1] [i+1,j−1]。在这2个选择中,对手必然选那个对先手不利的。
2)拿 j j j。接着对手也有2个选择,拿 i i i或 j − 1 j-1 j−1:拿 i i i,剩下 [ i + 1 , j − 1 ] [i+1, j-1] [i+1,j−1];拿 j − 1 j-1 j−1,剩下 [ i , j − 2 ] [i, j-2] [i,j−2]。
得到dp转移方程2:
d p [ i ] [ j ] = M a x ( V [ i ] + m i n ( d p [ i + 2 ] [ j ] , d p [ i + 1 ] [ j − 1 ] ) , V [ j ] + m i n ( d p [ i + 1 ] [ j − 1 ] , d p [ i ] [ j − 2 ] ) ) dp[i][j]=Max(V[i]+min(dp[i+2][j],dp[i+1][j-1]), V[j]+min(dp[i+1][j-1], dp[i][j-2])) dp[i][j]=Max(V[i]+min(dp[i+2][j],dp[i+1][j−1]),V[j]+min(dp[i+1][j−1],dp[i][j−2]))
d p [ i ] [ j ] = V [ i ] dp[i][j] = V[i] dp[i][j]=V[i] if j = = i j == i j==i
d p [ i ] [ j ] = m a x ( V [ i ] , V [ j ] ) dp[i][j] = max(V[i], V[j]) dp[i][j]=max(V[i],V[j]) if j = = i + 1 j == i+1 j==i+1
2.10 矩阵链乘法(Matrix Chain Multiplication)
背景知识:
(1)矩阵乘法。如果矩阵A、B能相乘,那么A的列数等于B的行数。设A是m行n列(记为m×n),B是n×u,那么乘积AB的行和列是m×u的,矩阵乘法AB需要做 m × n × u m×n×u m×n×u次乘法计算。(注意本小节的"×"符号有2个意思,分别表示矩阵和乘法。)
(2)矩阵乘法的结合律: ( A B ) C = A ( B C ) (AB)C = A(BC) (AB)C=A(BC)。括号体现了计算的先后顺序。
(3)在不同的括号下,矩阵乘法需要的乘法操作次数不同。以矩阵A、B、C的乘法为例,设A的行和列是m×n的,B是n×u,C是u×v,下面的两种计算方法,需要的乘法次数分别是:
( A B ) C (AB)C (AB)C,计算次数是 m × n × u + m × u × v m×n×u + m×u×v m×n×u+m×u×v
A ( B C ) A(BC) A(BC),计算次数是 m × n × v + n × u × v m×n×v + n×u×v m×n×v+n×u×v
两者的差是 ∣ m × n × ( u − v ) + u × v × ( m − n ) ∣ |m×n×(u-v)+u×v×(m-n)| ∣m×n×(u−v)+u×v×(m−n)∣,它可能是一个巨大的值。如果能知道哪一个括号方案是最优的,就能够大大减少计算量。
矩阵链乘法问题:给定一个数组 P [ ] P[] P[],其中 p [ i − 1 ] × p [ i ] p[i-1]×p[i] p[i−1]×p[i]表示矩阵 A i A_i Ai,输出最少的乘法次数,并输出此时的括号方案。
例如 p [ ] p[] p[] = {40, 20, 30, 10, 30},它表示4个矩阵:40×20,20×30,30×10,10×30。4个矩阵相乘,当括号方案是 ( A ( B C ) ) D (A(BC))D (A(BC))D时,有最少乘法次数26000。
如果读者学过区间DP,就会发现这是一个典型的区间DP问题。设链乘的矩阵是 A i A i + 1 … A j A_iA_{i+1}…A_j AiAi+1…Aj,即区间 [ i , j ] [i, j] [i,j],那么按结合率,可以把它分成2个子区间 [ i , k ] 、 [ k + 1 , j ] [i, k]、[k+1,j] [i,k]、[k+1,j],分别链乘,有:
A i A i + 1 … A j = ( A i . . . A k ) ( A k + 1 . . . A j ) A_iA_{i+1}…A_j = (A_i...A_k)(A_{k+1}...A_j) AiAi+1…Aj=(Ai...Ak)(Ak+1...Aj)
必定有一个 k k k,使得乘法次数最少,记这个 k k k为 k i , j k_{i,j} ki,j。并且记 A i , j A_{i,j} Ai,j为此时 A i A i + 1 … A j A_iA_{i+1}…A_j AiAi+1…Aj通过加括号后得到的一个最优方案,它被 k i , j k_{i,j} ki,j分开。
那么子链 A i A i + 1 … A k A_iA_{i+1}…A_k AiAi+1…Ak的方案 A i , k A_{i,k} Ai,k、子链 A k + 1 A k + 2 … A j A_{k+1}A_{k+2}…A_j Ak+1Ak+2…Aj的方案 A k + 1 , j A_{k+1, j} Ak+1,j也都是最优括号子方案。
这样就形成了递推关系:
A i , j = m i n { A i , k + A k + 1 , j + p i − 1 p k p j } A_{i,j} = min\{A_{i,k} + A_{k+1,j} + p_{i-1}p_kp_j\} Ai,j=min{Ai,k+Ak+1,j+pi−1pkpj}
用二维矩阵 d p [ i ] [ j ] dp[i][j] dp[i][j]来表示 A i , j A_{i,j} Ai,j,得到转移方程为:
d p [ i ] [ j ] = { 0 , i=j m i n { d p [ i ] [ k ] + d p [ k + 1 ] [ j ] + p [ i − 1 ] p [ k ] p [ j ] } , i≤k
d p [ 1 ] [ n ] dp[1][n] dp[1][n]就是答案,即最少乘法次数。
d p [ i ] [ j ] dp[i][j] dp[i][j]的编码实现,可以套用区间DP模板,遍历 i 、 j 、 k i、j、k i、j、k,复杂度是 O ( n 3 ) O(n^3) O(n3)。
区间DP常常可以用四边形不等式优化,但是这一题不行,因为它不符合四边形不等式优化所需要的单调性条件。
习题: poj 1651 Multiplication Puzzle http://poj.org/problem?id=1651
问题列表来自:https://www.geeksforgeeks.org/top-20-dynamic-programming-interview-questions/ ↩︎
还有一种DP方案,参考:https://www.geeksforgeeks.org/optimal-strategy-for-a-game-set-2/ ↩︎