动森大头菜价格变化分析（1）——不同价格走势的变换

0

想后面怎么做的时候老是按过程式的方法在想，没法套到MMA的思路上，就先试着用Python看能不能把整个思路搭起来，后面再看用不用MMA
实现一下吧

事情起于这篇文章：
《集合啦！动物森友会》大头菜背后的那些事儿
有人反编译了动物之森中控制大头菜价格变化的代码。虽然佛系如我连每天按时上线看下大头菜价格都做不到，但用这个例子去学习些新知识还是能为这个漫长的假期增添些乐趣吧。

上面链接中的文章我认为可以分为三部分：

1. 每周大头菜价格走势的变换方法
2. 不同价格模型的具体内容
3. 如何预测大头菜价格并分析当周价格模型

在本文中我尝试利用Mathematica 去还原上述的第一部分，即上周价格走势对当周价格走势的影响。

1

连接中的文章介绍了四种在动森中用于控制一周之内大头菜价格走势变化的模型，分别是 波动性 、3期型、4期型 以及 持续下降型。在这里先不对各个价格模型的具体内涵进行介绍。

通过反编译发现上周的价格走势会对影响不同价格走势在下周出现的概率，具体概率分布表如下：

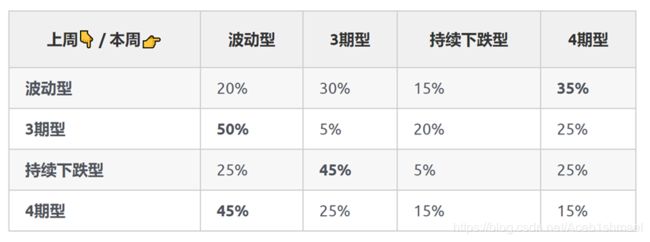
表中的第一列代表上周大头菜的价格走势，第一行则代表本周价格的可能走势，除此之外表中各单元代表在上周大头菜价格走势为其同行对应的模型的基础上，本周大头菜价格的走势是与其同列的第一行价格模型的概率。例如表中的第3行第2列数值为50%的单元格，代表的意思是在上周价格为3期型的前提下，本周价格趋势为波动型的概率为50%。初次之外价格走势还有一个条件是大头菜投资的第一周价格模型为4期型。

可以发现每周价格的走势仅与前一周的价格走势有关，同时当周出现何种价格走势受到一个固定概率表的控制，符合 马尔可夫过程 后一状态仅与其相邻的前一状态有关的性质。

2

Mathematica 本身内涵了大量与随机过程有关的函数方法，其中也包含多种实现马尔可夫过程的方法。

2.1

具体到大头菜价格模型这个例子来说，其适用DiscreteMarkovProcess(离散马可夫过程) 这一方法。在Mathmatica 中DiscreteMarkovProcess 有不同的应用方式，我选择使用：
DiscreteMarkovProcess[i,m]
表示转移矩阵为 m 和初始状态为i的离散时间有限状态马可夫过程.，对应于大头菜上述表格即为价格走势的转移矩阵，整个过程的初始状态则为 4期型 。

2.2

利用DiscreteMarkovProcess 对大头菜价格走势进行建模：

pattenShift=DiscreteMarkovProcess[4,{{0.2,0.3,0.15,0.35},{0.5,0.05,0.2,0.25},{0.25,0.45,0.05,0.25},{0.45,0.25,0.15,0.15}}];

RandomFunction 可对此过程进行模拟，例如我们对前100周价格走势的情况进行模拟，并以散点图显示其中一次模拟结果：

ListPlot[RandomFunction[pattenShift,{0,100}],Filling->Axis,Ticks->{Automatic, {{1,“波动型”},{2,“3期型”},{3,“持续下降型”},{4,“4期型”}}}]

我们还可以用有向图的形式展示上面的价格走势变化过程：

Graph[cross,VertexLabels->{1->“波动型”,2->“3期型”,3->“持续下降型”,4->“4期型”},VertexSize->Small,EdgeLabels->With[{sm=MarkovProcessProperties[pattenShift,“TransitionMatrix”]},Flatten@Table[DirectedEdge[i,j]->sm[[i,j]],{i,4},{j,4}]],ImageSize->Large]

在图中4个黄色节点代表价格走势的4种可能，有向线的指向代表从上一周的价格走势模型向下一周价格走势模型变化的过程，不同有向线上的数值代表不同可能变化的概率。

此外还能够获得此过程的概率密度函数：

PDF[pattenShift[n], k] // PiecewiseExpand

$\begin{array}{cc}\{& \begin{array}{cc}0.101533\left(2.43627+1.(-0.317323{)}^n-1.31345(-0.186112{)}^n-2.12282(-0.0465646{)}^n\right)& k=2\\ -0.144804\left(1.(-0.317323{)}^n+2.39477(-0.186112{)}^n-1.00342(-0.0465646{)}^n-2.39135\right)& k=1\\ 0.0666309\left(3.88337+1.(-0.317323{)}^n+6.04373(-0.186112{)}^n+4.08095(-0.0465646{)}^n\right)& k=4\\ -0.02336\left(1.(-0.317323{)}^n-3.31477(-0.186112{)}^n+8.63357(-0.0465646{)}^n-6.3188\right)& k=3\end{array}\end{array}$
第3周不同大头菜价格模型的可能概率为：

DiscretePlot[PDF[pattenShift[2],k],{k,1,4},Ticks->{ {{1,“波动型”},{2,“3期型”},{3,“持续下降型”},{4,“4期型”}},Automatic}]

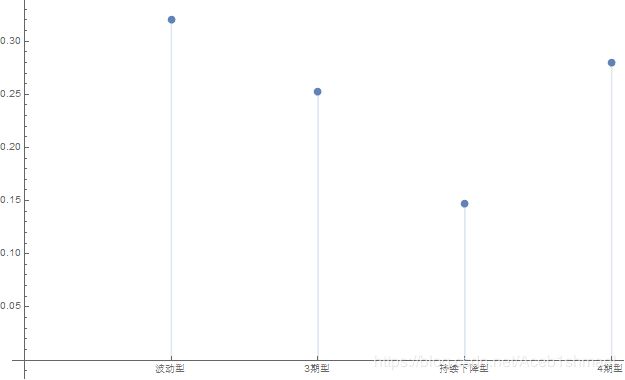
波动型的可能性较大，其次为4期型，后两位为3期型与持续下降型。
前100周大头菜价格走势曲不同模型的可能性为：

DiscretePlot3D[PDF[pattenShift[n],k],{n,0,100},{k,1,4},Ticks->{Automatic, {{1,“波动型”},{2,“3期型”},{3,“持续下降型”},{4,“4期型”}},Automatic}]

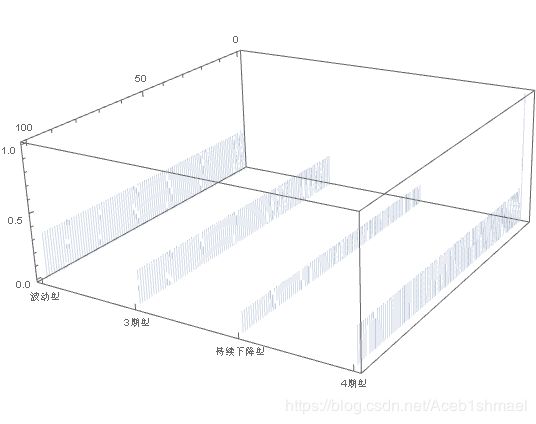
不同模型的概率分布和单独一周的类似。

3

利用离散马尔可夫过程实现了对不同周大头菜价格走势变化的模拟，之后我会继续尝试利用Mathematica 研究大头菜的价格变化，之后的计划是在还原不同价格走势模型，尝试预测大头菜价格变化。