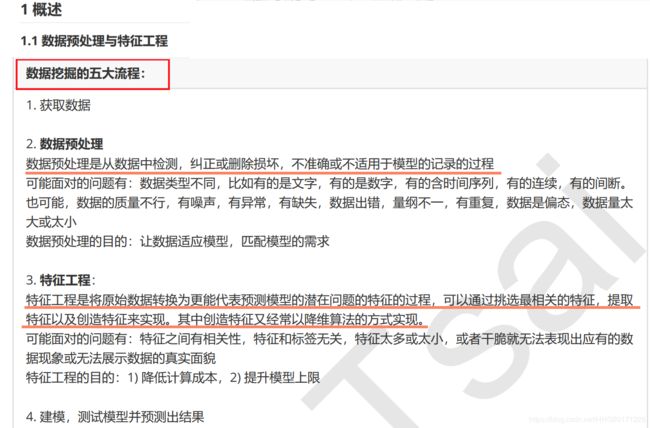
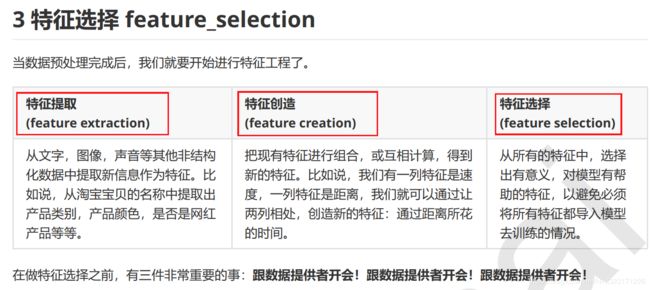
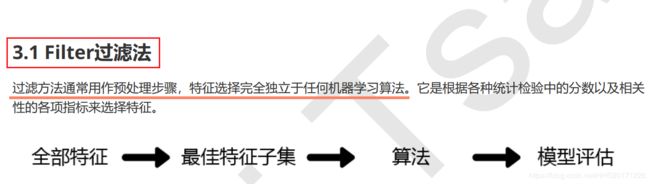
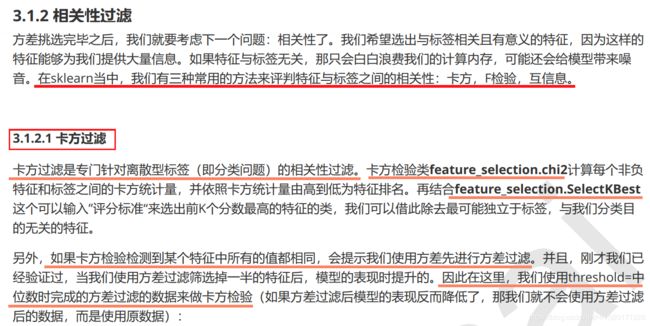
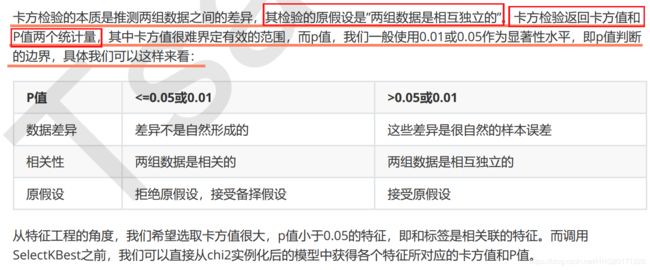
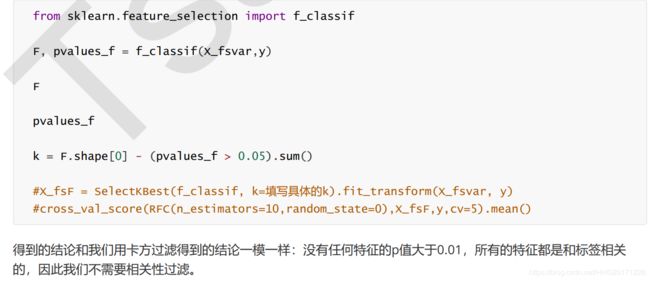
sklearn中的数据预处理和特征工程

from sklearn.preprocessing import MinMaxScaler
data = [[-1, 2], [-0.5, 6], [0, 10], [1, 18]]

import pandas as pd
pd.DataFrame(data)

#实现归一化
scaler = MinMaxScaler() #实例化
scaler = scaler.fit(data) #fit，在这里本质是生成min(x)和max(x)
result = scaler.transform(data) #通过接口导出结果
result


result_ = scaler.fit_transform(data) #训练和导出结果一步达成
scaler.inverse_transform(result) #将归一化后的结果逆转


#使用MinMaxScaler的参数feature_range实现将数据归一化到[0,1]以外的范围中
data = [[-1, 2], [-0.5, 6], [0, 10], [1, 18]]
scaler = MinMaxScaler(feature_range=[5,10]) #（[]5,10]的范围） 依然实例化

result = scaler.fit_transform(data) #fit_transform一步导出结果
result
#当X中的特征数量非常多的时候，fit会报错并表示，数据量太大了计算不了
#此时使用partial_fit作为训练接口
#scaler = scaler.partial_fit(data)

使用numpy来实现归一化

import numpy as np
X = np.array([[-1, 2], [-0.5, 6], [0, 10], [1, 18]])

#归一化
X_nor = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))
X_nor

#逆转归一化
X_returned = X_nor * (X.max(axis=0) - X.min(axis=0)) + X.min(axis=0)
X_returned

.mean_查看均值的属性mean_
.var_查看方差的属性var_

from sklearn.preprocessing import StandardScaler
data = [[-1, 2], [-0.5, 6], [0, 10], [1, 18]]

scaler = StandardScaler() #实例化
scaler.fit(data) #fit，本质是生成均值和方差

scaler.mean_ #查看均值的属性mean_
#--->array([-0.125,  9.   ])
scaler.var_ #查看方差的属性var_
#--->array([ 0.546875, 35.      ])

x_std = scaler.transform(data) #通过接口导出结果
x_std.mean() #导出的结果是一个数组，用mean()查看均值
#--->0.0
x_std.std() #用std()查看方差
#--->1.0

scaler.fit_transform(data) #使用fit_transform(data)一步达成结果

scaler.inverse_transform(x_std) #使用inverse_transform逆转标准化

import pandas as pd
data = pd.read_csv(r"Narrativedata.csv",index_col=0)

#填补年龄
Age = data.loc[:,"Age"].values.reshape(-1,1) #sklearn当中特征矩阵必须是二维

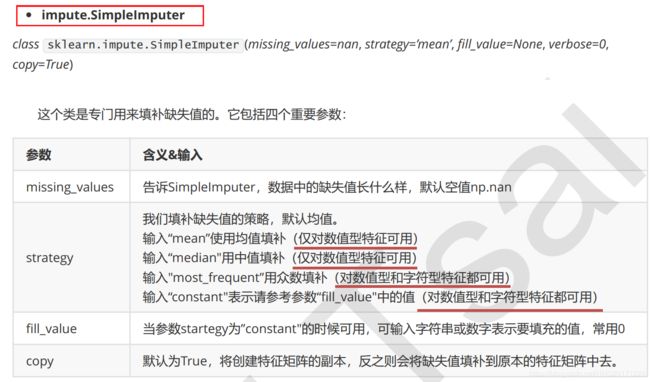
from sklearn.impute import SimpleImputer

imp_mean = SimpleImputer() #实例化，默认均值填补

imp_median = SimpleImputer(strategy="median") #用中位数填补

imp_0 = SimpleImputer(strategy="constant",fill_value=0) #用0填补

imp_mean = imp_mean.fit_transform(Age) #fit_transform一步完成调取结果
imp_median = imp_median.fit_transform(Age)
imp_0 = imp_0.fit_transform(Age)

#在这里我们使用中位数填补Age
data.loc[:,"Age"] = imp_median

#使用众数填补Embarked
Embarked = data.loc[:,"Embarked"].values.reshape(-1,1)

imp_mode = SimpleImputer(strategy = "most_frequent")
data.loc[:,"Embarked"] = imp_mode.fit_transform(Embarked)

用Pandas和Numpy进行填补其实更加简单

data.loc[:,"Age"] = data.loc[:,"Age"].fillna(data.loc[:,"Age"].median())
#.fillna 在DataFrame里面直接进行填补

data.dropna(axis=0,inplace=True)
#.dropna(axis=0)删除所有有缺失值的行，.dropna(axis=1)删除所有有缺失值的列
#参数inplace，为True表示在原数据集上进行修改，为False表示生成一个复制对象，不修改原数据，默认False

#属性.classes_查看标签中究竟有多少类别

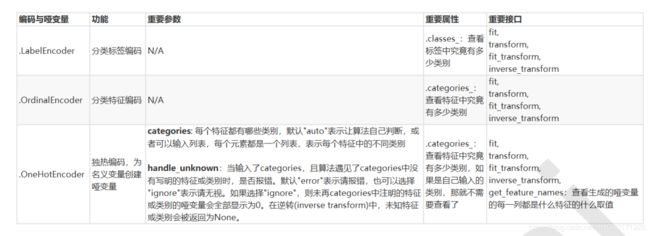
from sklearn.preprocessing import LabelEncoder
y = data.iloc[:,-1] #要输入的是标签，不是特征矩阵，所以允许一维
le = LabelEncoder() #实例化
le = le.fit(y) #导入数据
label = le.transform(y) #transform接口调取结果
le.classes_ #属性.classes_查看标签中究竟有多少类别
label #查看获取的结果label
le.fit_transform(y) #也可以直接fit_transform一步到位
le.inverse_transform(label) #使用inverse_transform可以逆转

data.iloc[:,-1] = label #让标签等于我们运行出来的结果
data.head()


#直接这么写：
from sklearn.preprocessing import LabelEncoder
data.iloc[:,-1] = LabelEncoder().fit_transform(data.iloc[:,-1])

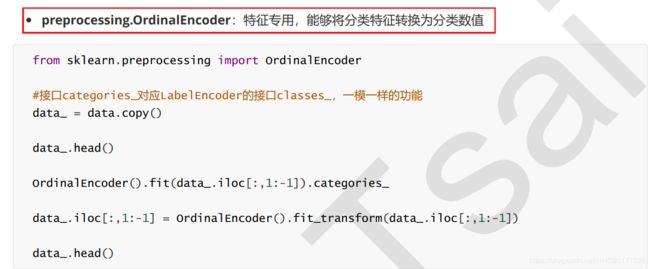
from sklearn.preprocessing import OneHotEncoder
X = data.iloc[:,1:-1]
enc = OneHotEncoder(categories='auto').fit(X)
result = enc.transform(X).toarray()
result
#依然可以直接一步到位，但为了给大家展示模型属性，所以还是写成了三步
OneHotEncoder(categories='auto').fit_transform(X).toarray()
#依然可以还原
pd.DataFrame(enc.inverse_transform(result))
enc.get_feature_names()
result
result.shape
#axis=1,表示跨行进行合并，也就是将量表左右相连，如果是axis=0，就是将量表上下相连
newdata = pd.concat([data,pd.DataFrame(result)],axis=1)
newdata.head()
newdata.drop(["Sex","Embarked"],axis=1,inplace=True)
newdata.columns =
["Age","Survived","Female","Male","Embarked_C","Embarked_Q","Embarked_S"]
newdata.head()

#将年龄二值化
data_2 = data.copy()
from sklearn.preprocessing import Binarizer
X = data_2.iloc[:,0].values.reshape(-1,1) #类为特征专用，所以不能使用一维数组
transformer = Binarizer(threshold=30).fit_transform(X)
transformer

from sklearn.preprocessing import KBinsDiscretizer
X = data.iloc[:,0].values.reshape(-1,1)
est = KBinsDiscretizer(n_bins=3, encode='ordinal', strategy='uniform')
est.fit_transform(X)
#查看转换后分的箱：变成了一列中的三箱
set(est.fit_transform(X).ravel())
est = KBinsDiscretizer(n_bins=3, encode='onehot', strategy='uniform')
#查看转换后分的箱：变成了哑变量
est.fit_transform(X).toarray()

import numpy as np
X_fsvar = VarianceThreshold(np.median(X.var().values)).fit_transform(X)
X.var().values
np.median(X.var().values)
X_fsvar.shape

from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2

#假设在这里我一直我需要300个特征
X_fschi = SelectKBest(chi2, k=300).fit_transform(X_fsvar, y)
X_fschi.shape

Rescaling (min-max normalization)（最小-最大归一化）

Also known as min-max scaling or min-max normalization, is the simplest method and consists in rescaling the range of features to scale the range in [0, 1] or [−1, 1]. Selecting the target range depends on the nature of the data. The general formula for a min-max of [0, 1] is given as:

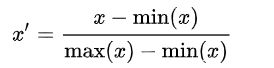
where x is an original value, x’ is the normalized value. For example, suppose that we have the students’ weight data, and the students’ weights span [160 pounds, 200 pounds]. To rescale this data, we first subtract 160 from each student’s weight and divide the result by 40 (the difference between the maximum and minimum weights).
To rescale a range between an arbitrary set of values [a, b], the formula becomes:

Mean normalization（平均归一化）

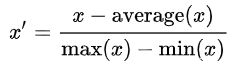
where {\displaystyle x}x is an original value, x’ is the normalized value. There is another form of the mean normalization which is when we divide by the standard deviation which is also called standardization.

Standardization (Z-score Normalization)

数据预处理需要根据数据本身的特性进行，有不同的格式和不同的要求，有缺失值要填，有无效数据的要剔除，有冗余维的要选，这些步骤都和数据本身的特性紧密相关。数据预处理大致分为三个步骤：数据的准备，数据的转换，数据的输出。数据处理是系统工程的基本环节，也是提高算法准确度的有效手段。因此，为了提高算法模型的准确度，在机器学习中也要根据算法的特征和数据的特征对数据进行转换。
数据转换方法：
  1. 调整数据尺度
  2. 正态化数据
  3. 标准化数据
  4. 二值数据

1. 调整数据尺度

在scikit-learn中，可以通过MinMaxScaler 类来调整数据尺度。将不同计量单位地数据统一成相同的尺度，利于对事物地分类或分组。实际上，MinMaxScaler是将属性缩放到一个指定范围，或者对数据进行标准化并将数据都聚集到0附近，方差为1。数据尺度的统一，通常能够提高与距离有关的算法的准确度（如`K近邻算法）。

#调整数据尺度
from pandas import read_csv
from numpy import set_printoptions
from sklearn.preprocessing import MinMaxScaler
#导入数据
filename = 'indians.csv'
names = ['preg','plas','pres','skin','test','mass','pedi','age','class']
data = read_csv(filename,names=names)
#将数据分为输入数据和输出结果
array = data.values
X = array[:,0:8]
Y = array[:,8]
transformer = MinMaxScaler(feature_range=(0,1))
#数据转换
newX = transformer.fit_transform(X)
#设定数据的打印格式
set_printoptions(precision=3)#小数点后精度第3位
print(newX)

一般是把数据映射到 [ 0，1 ] ，但也有归一到 [ -1，1 ] 的情况，两种情况在Python中分别可以通过MinMaxScaler 或者 MaxAbsScaler方法来实现。

MinMaxScaler：归一到 [ 0，1 ]

原理

从原理中我们注意到有一个axis=0，这表示MinMaxScaler方法默认是对每一列做这样的归一化操作，这也比较符合实际应用。

eg：将数据归一到 [ 0，1 ]

from sklearn import preprocessing
import numpy as np

x = np.array([[3., -1., 2., 613.],
              [2., 0., 0., 232],
              [0., 1., -1., 113],
              [1., 2., -3., 489]])

min_max_scaler = preprocessing.MinMaxScaler()
x_minmax = min_max_scaler.fit_transform(x)
print(x_minmax)
'''
[[1.         0.         1.         1.        ]
 [0.66666667 0.33333333 0.6        0.238     ]
 [0.         0.66666667 0.4        0.        ]
 [0.33333333 1.         0.         0.752     ]]
'''

每一列特征中的最小值变成了0，最大值变成了1.
如果有新的测试数据进来，也想做同样的转换，那么将新的测试数据添加到原数据末尾即可

y = [7., 1., -4., 987]#新的测试数据
x.append(y)#将y添加到x的末尾
print('x ：\n', x)
x_minmax = min_max_scaler.fit_transform(x)

MaxAbsScaler：归一到 [ -1，1 ]

原理与MinMaxScaler相似，

from sklearn import preprocessing
import numpy as np
 
x = np.array([[3., -1., 2., 613.],
              [2., 0., 0., 232],
              [0., 1., -1., 113],
              [1., 2., -3., 489]])
max_abs_scaler = preprocessing.MaxAbsScaler()
x_train_maxsbs = max_abs_scaler.fit_transform(x)
x_train_maxsbs

2.正态化数据

正态化数据是有效的处理符合高斯分布的数据的手段，输出结果以0为中位数，方差为1，并作为假定数据符合高斯分布的算法的输入。这些算法有线性回归，逻辑回归和线性判别分析等。可通过scikit-learn提供的StandardScaler类来进行正态化数据处理。

公式为：(X-X_mean)/X_std 计算时对每个属性/每列分别进行.
将数据按其属性(按列进行)减去其均值，然后除以其方差。最后得到的结果是，对每个属性/每列来说所有数据都聚集在0附近，方差值为1。
方法一：使用sklearn.preprocessing.scale()函数

sklearn.preprocessing.scale(X, axis=0, with_mean=True,with_std=True,copy=True)
参数解释：
	
	X：数组或者矩阵
	axis：int类型，初始值为0，axis用来计算均值 means 和标准方差 standard deviations. 如果是0，则单独的标准化每个特征（列），如果是1，则标准化每个观测样本（行）。
	with_mean: boolean类型，默认为True，表示将数据均值规范到0
	with_std: boolean类型，默认为True，表示将数据方差规范到1

方法说明：

• X.mean(axis=0)用来计算数据X每个特征的均值；
• X.std(axis=0)用来计算数据X每个特征的方差；
• preprocessing.scale(X)直接标准化数据X。

from sklearn import preprocessing 
import numpy as np
X = np.array([[ 1., -1.,  2.],
              [ 2.,  0.,  0.],
              [ 0.,  1., -1.]])
# calculate mean
X_mean = X.mean(axis=0)
# calculate variance 
X_std = X.std(axis=0)
# standardize X
X1 = (X-X_mean)/X_std
# use function preprocessing.scale to standardize X
X_scale = preprocessing.scale(X)

最后X_scale的值和X1的值是一样的，前面是单独的使用数学公式来计算，主要是为了形成一个对比，能够更好的理解scale()方法。

方法2：sklearn.preprocessing.StandardScaler类

#正态化数据
from pandas import read_csv
from numpy import set_printoptions
from sklearn.preprocessing import StandardScaler
#导入数据
filename = r'ima_data.csv'
names = ['preg','plas','pres','skin','test','mass','pedi','age','class']
data = read_csv(filename,names=names)
#将数据分为输入数据和输出结果
array = data.values
X = array[:,0:8]
Y = array[:,8]
transformer = StandardScaler().fit(X)
#数据转换
# print(transformer.mean_)
# print(transformer.std_)
newX = transformer.transform(X)
set_printoptions(precision=3)
print(newX)

#注 ：1）若设置with_mean=False 或者 with_std=False，则不做centering 或者scaling处理。

3.数据标准化/归一化normalization

标准化数据处理是将每一行的数据的距离处理为1(在线性代数中矢量距离为1)的数据又叫做“归一元”处理，适合处理稀疏数据（具有很多为0的数据），归一元处理的数据对使用权重输入的神经网络和使用距离的K近邻算法的准确度的提升有显著作用。使用scikit-learn中的Normalizer类实现。

数据的标准化（normalization）是将数据按比例缩放，使之落入一个小的特定区间。在某些比较和评价的指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。

目前数据标准化方法有多种，归结起来可以分为直线型方法(如极值法、标准差法)、折线型方法(如三折线法)、曲线型方法(如半正态性分布)。不同的标准化方法，对系统的评价结果会产生不同的影响，然而不幸的是，在数据标准化方法的选择上，还没有通用的法则可以遵循。

其中最典型的就是数据的归一化处理，即将数据统一映射到[0,1]区间上。

归一化方法有两种形式，一种是把数变为（0，1）之间的小数，一种是把有量纲表达式变为无量纲表达式。

1、线性函数归一化(Min-Max scaling)

线性函数将原始数据线性化的方法转换到[0 1]的范围，归一化公式如下：

该方法实现对原始数据的等比例缩放，其中Xnorm为归一化后的数据，X为原始数据，Xmax、Xmin分别为原始数据集的最大值和最小值。

2、0均值标准化(Z-score standardization)

0均值归一化方法将原始数据集归一化为均值为0、方差1的数据集，归一化公式如下：

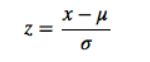
其中，μ、σ分别为原始数据集的均值和方差。该种归一化方式要求原始数据的分布可以近似为高斯分布，否则归一化的效果会变得很糟糕。
以上为两种比较普通但是常用的归一化技术，那这两种归一化的应用场景是怎么样的呢？什么时候第一种方法比较好、什么时候第二种方法比较好呢？下面做一个简要的分析概括：
1、在分类、聚类算法中，需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候，第二种方法(Z-score standardization)表现更好。
2、在不涉及距离度量、协方差计算、数据不符合正太分布的时候，可以使用第一种方法或其他归一化方法。比如图像处理中，将RGB图像转换为灰度图像后将其值限定在[0 255]的范围。

# 标准化数据
from pandas import read_csv
from numpy import set_printoptions
from sklearn.preprocessing import Normalizer
# 导入数据
filename = 'pima_data.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(filename, names=names)
# 将数据分为输入数据和输出结果
array = data.values
X = array[:, 0:8]
Y = array[:, 8]
scaler = Normalizer().fit(X)
# 数据转换
rescaledX = scaler.transform(X)
# 设定数据的打印格式
set_printoptions(precision=3)
print(rescaledX)

4.二值数据

二值数据是使用值将数据转化为二值，大于阈值设置为1，小于阈值设置为0。这个过程被叫做二分数据或阈值转换。在生成明确值或特征工程增加属性时候使用，使用scikit-learn中的Binarizer类实现。

# 二值数据
from pandas import read_csv
from numpy import set_printoptions
from sklearn.preprocessing import Binarizer
# 导入数据
filename = 'pima_data.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(filename, names=names)
# 将数据分为输入数据和输出结果
array = data.values
X = array[:, 0:8]
Y = array[:, 8]
transform = Binarizer(threshold=0.0).fit(X)
# 数据转换
newX = transform.transform(X)
# 设定数据的打印格式
set_printoptions(precision=3)
print(newX)

二值化器(binarizer)的阈值是可以被调节的:

from  sklearn.preprocessing import  Binarizer
from  sklearn import preprocessing

X = [[ 1., -1.,  2.],
      [ 2.,  0.,  0.],
      [ 0.,  1., -1.]]

transform = Binarizer(threshold=0.0)
newX=transform.fit_transform(X)
# print(mm)

# transform = Binarizer(threshold=0.0).fit(X)
# newX = transform.transform(X)

binarizer = preprocessing.Binarizer().fit(X)  # fit does nothing
print(binarizer)
#Binarizer(copy=True, threshold=0.0)

print(binarizer.transform(X))
'''
[[1. 0. 1.]
 [1. 0. 0.]
 [0. 1. 0.]]
'''

binarizer = preprocessing.Binarizer(threshold=1.1)
print(binarizer.transform(X))
'''
[[0. 0. 1.]
 [1. 0. 0.]
 [0. 0. 0.]]
'''

python 简单实现

import  numpy as np
threshold=3
X= np.array([1,2,3,1,2,4,5,0,3,6,2])
print(X> threshold)         
#[False False False False False  True  True False False  True False]
cond = X > threshold
not_cond = np.logical_not(cond)
X[cond] = 1
X[not_cond] = 0
print(X)