函数使用
为什么要使用函数 ?
一个较为复杂的系统往往需要若干个子系统,然后分别对这些子系统进行开发。通常将相对独立的,经常使用的功能抽象为函数,函数编写好以后可以被重复利用,这样有利于代码重用,提升开发效率,增强程序可靠性,也便于分工合作和修改。---c++语言程序设计函数部分
从上面这段话中我们可以提炼出使用函数的几个优点!
- 代码重复利用
- 代码分区分块,便于修改和维护
- 增强程序的可靠性
下面我就用一个简单的打印程序来说明函数的方便性。
#include using namespace std;void print(int a) {cout << a << endl;}
int main()
{
int a, b,sum;a = 3, b = 4;sum = a + b; print(sum); sum = b - a; print(sum); return 0; } 这段代码就体现了函数的分块性和代码重复利用性,每当我看一下代码计算过程的值,我就调用一下print函数,就不需要在反复写cout语句了,其次打印函数和主函数是分开的,维护起来只用看有问题的部分,互不影响。
为什么要用函数重载 ?
两个以上的函数,具有相同的函数名,但是形参的个数或者类型不同,编译器根据实参和形参类型及个数的最佳匹配,自动确定调用那一个函数,这就是函数的重载。 ---c++语言程序设计函数重载部分
从课本上的定义来看我们也可以提炼出函数重载的优点
- 具有相似操作的函数可以取相同函数名,让系统去判断具体执行那一个函数。
- 减少了命名的麻烦,维护时只需看参数来判断要修改的函数。
- 体现了面向对象程序设计语言的多态性。
举例
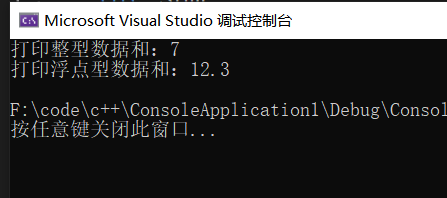
#include using namespace std;void print(int a) { cout << "打印整型数据和:" << a << endl;}void print(double a) { cout << "打印浮点型数据和:" << a << endl;}int main(){ int a = 3, b = 4; int sum; sum = a + b; print(sum);
double x = 3.4, y = 8.9; double sums; sums = x + y; print(sums); return 0;}
这段代码通过一个简单的打印体现出了,系统通过形参的不同调用不同print函数,从而实现了函数的重载。
什么是值传递?
值传递,顾名思义,就是传递数的值,下面我用一个交换的例子来体现。
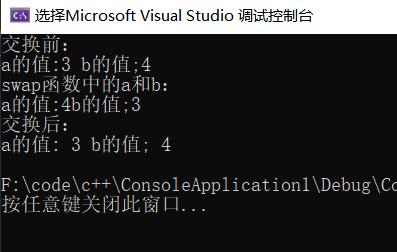
#include using namespace std;void swap(int a, int b) { int t; t = a; a = b; b = t; cout << "swap函数中的a和b:" << endl; cout << "a的值:" << a << "b的值;" << b << endl;}int main(){ int a, b; a = 3; b = 4; cout << "交换前:" << endl; cout << "a的值:" << a << " b的值;" << b << endl; swap(a, b); cout << "交换后:" << endl; cout << "a的值: " << a << " b的值; " << b << endl; return 0;}
从程序执行结果可以看到,主函数中的a和b的值在经过swap函数处理后,没有什么变化,但是在swap函数中a和b的值却发生了改变,这是因为在主函数和swap函数中的a和b不是同一个a和b,他们在内存中分别占有不同的内存空间,调用swap时只是把主函数中a和b的值传递过去,所以叫做值传递。
什么是地址传递?
地址传递,就是将变量在内存的存储地址传递到处理函数中,从而达到改变主函数对应变量的值的效果。
还是以数值交换为例
#include
using namespace std;
void swap(int *a, int *b) {
int t;
t = *a;
*a = *b;
*b = t;
cout << "swap函数中的a和b:" << endl;
cout << "a的值:" << a << "b的值;" << b << endl;
}
int main()
{
int a, b;
a = 3;
b = 4;
cout << "交换前:" << endl;
cout << "a的值:" << a << " b的值;" << b << endl;
swap(&a, &b);
cout << "交换后:" << endl;
cout << "a的值: " << a << " b的值; " << b << endl;
return 0;
} 这一次就通过调用swap交换了主函数中a和b值,这一次我传递到swap函数中的参数是&a和&b,作用就是把a和b的地址传递到swap函数中,这里主函数和swap函数中的a和b是同一个a和b,所以起到了交换数值的效果。
递归函数设计
递归函数,就是函数自己调用自己本身,如“软件=程序+软件工程”这就可以算是递归定义,因为定义的本身还是使用了自己本省
学习递归函数主要分三个步骤
- 找到重复执行的部分
- 找到终止条件
- 编写代码
以经典的汉诺塔问题为例
汉诺塔:汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
分析:
- 重复的操作就是将n-1个盘子按要求借助中间柱子移动到目的柱子
- 终止条件就是把最后一个盘子移动到目的柱子
- 编写代码
#include
using namespace std;
void move(char src, char dest) {
cout << src << "-->" << dest << endl;
}
void hanoi(int n, char src, char medium, char dest) {
if (n == 1) {
move(src, dest);
}
else
{
hanoi(n - 1, src, dest, medium);
move(src, dest);
hanoi(n - 1,medium,src, dest);
}
}
int main()
{
int m;
cout << "输入需要移动的盘子:";
cin >> m;
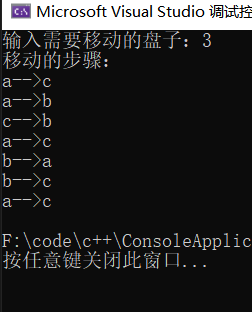
cout << "移动的步骤:" << endl;
hanoi(m,'a','b','c');
return 0;
}
具体分析过程:
想要把N个盘子从初始柱移动到目的柱,我不知道该怎么移动,但是如果如果初始柱只有一个盘子,我直接就可以移动到目的柱,所以根据这个想法,我就根据这个想法把柱子的个数先减到一个,移动过去后,在加一个,以此类推,最后把N个盘子移动过去。