02_End-to-End Machine Learning Project_03_stats.sem_ppf_CategoricalEncoder_RandomizedSearchCV_joblib
02_End-to-End Machine Learning Project
https://blog.csdn.net/Linli522362242/article/details/103387527
02_End-to-End Machine Learning Project_02
https://blog.csdn.net/Linli522362242/article/details/103587172
We can compute a 95% confidence interval for the test RMSE:
the Root Mean Square Error (RMSE). It measures the standard deviation of the errors the system makes in its predictions. For example, an RMSE equal to 50,000 means that about 68% of the system’s predictions fall within $50,000 of the actual value, and about 95% of the predictions fall within $100,000 of the actual value. Equation 2-1 shows the mathematical formula to compute the RMSE.
When a feature has a bell-shaped normal distribution (also called a Gaussian distribution), which is very common,
the “68-95-99.7” rule applies: about 68% of the values fall within 1σ of the mean, 95% within 2σ, and 99.7% within 3σ.
from scipy import stats
confidence = 0.95
#residual=yi-y_hat_i
squared_errors = (final_predictions - y_test)**2
np.sqrt( stats.t.interval(confidence,
len(squared_errors)-1, #df=degrees of freedom=number of samples -1
loc = squared_errors.mean(), #the sample means
scale = stats.sem(squared_errors) #the standard error of the mean of the samples
)
)![]()
##########################
We could compute the interval manually like this:
stats.sem(squared_errors)

![]()
![]()
squared_errors_standard_deviation = np.sqrt( np.sum( ( np.array(squared_errors).reshape(length,1) - \
np.tile([squared_errors_mean],[1, length]).T
)**2
)/(length-1)
)
standard_error_of_mean=squared_errors_standard_deviation/np.sqrt(length)
standard_error_of_mean #for Square Errors![]()
confidence = 0.95
(1-confidence)/2=![]()
![]()
![]()
1.96 is actually an approximation
standard_error_of_mean=squared_errors_standard_deviation/np.sqrt(length)
![]()
n = len(squared_errors)
mean = squared_errors.mean()
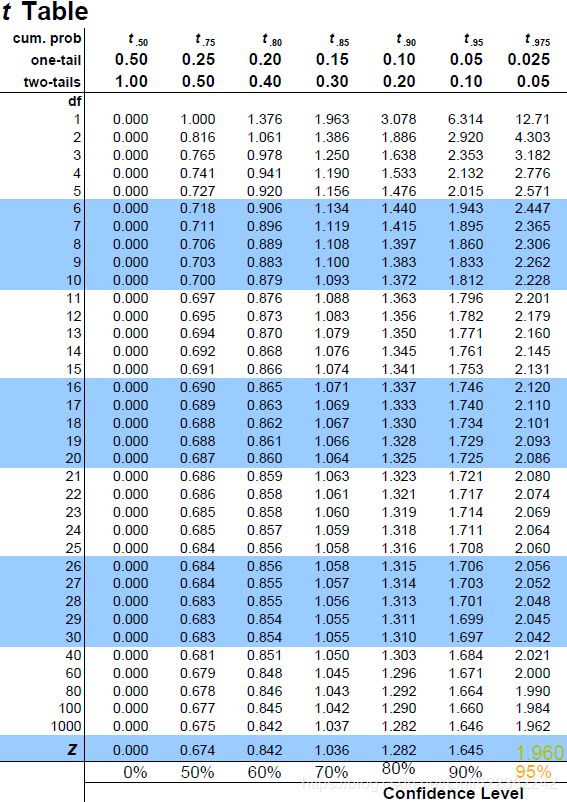
zscore = stats.norm.ppf( (1+confidence)/2 ) #chek Z Table: 1.96
#zscore =1.959963984540054
#ddof : int, default 1
# Delta Degrees of Freedom. The divisor used in calculations is N - ddof,
# where N represents the number of elements.
print(np.sqrt(mean-tscore * squared_errors.std(ddof=1) /np.sqrt(n)),
np.sqrt(mean+tscore * squared_errors.std(ddof=1) /np.sqrt(n))
)![]()
##############################
We could compute the interval manually like this:
| ppf(q, df, loc=0, scale=1) |
Percent point function (inverse of |
https://www.itl.nist.gov/div898/handbook/eda/section3/eda362.htm![]()
#The percent point function (ppf) is the inverse of the cumulative distribution function
n = len(squared_errors)
mean = squared_errors.mean()
#0.95 #>1000
tscore = stats.t.ppf((1+confidence)/2, df=n-1) # check t Table: 1.96
#tscore=1.9605389676490623
#ddof : int, default 1
# Delta Degrees of Freedom. The divisor used in calculations is N - ddof,
# where N represents the number of elements.
print(np.sqrt(mean-tscore * squared_errors.std(ddof=1) /np.sqrt(n)),
np.sqrt(mean+tscore * squared_errors.std(ddof=1) /np.sqrt(n))
)![]()
##########################################################################
Extra material
A full pipeline with both preparation and prediction
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.utils import check_array
from sklearn.preprocessing import LabelEncoder
from scipy import sparse
class CategoricalEncoder(BaseEstimator, TransformerMixin):
def __init__(self, encoding='onehot', categories='auto', dtype=np.float64, handle_unknown='error'):
self.encoding = encoding
self.categories = categories
self.dtype = dtype
self.handle_unknown = handle_unknown
def fit(self, X, y=None):
"""Fit the CategoricalEncoder to X.
Parameters
----------
X : array-like, shape [n_samples, n_feature]
The data to determine the categories of each feature.
Returns
-------
self
"""
if self.encoding not in ['onehot', 'onehot-dense', 'ordinal']:
template = ("encoding should be either 'onehot', 'onehot-dense' or 'ordinal', got %s")
raise ValueError(template % self.handle_unknown)
if self.handle_unknown not in ['error', 'ignore']:
template = ("handle_unknown should be either 'error' or 'ignore', got %s")
raise ValueError(template % self.handle_unknown)
if self.encoding == 'ordinal' and self.handle_unknown == 'ignore':
raise ValueError("handle_unknown='ignore' is not supported for encoding='ordinal'")
#check_array: By default, the input(here is X) is converted to an at least 2D numpy array.
#If the dtype of the array is object, attempt converting to float, raising on failure.
#csc_matrix: https://docs.scipy.org/doc/scipy/reference/generated/scipy.sparse.csc_matrix.html
X = check_array(X, dtype=np.object, accept_sparse='csc', copy=True)
#print(X)
#[['<1H OCEAN']
#['<1H OCEAN']
#['NEAR OCEAN']
#...
#['INLAND']
#['<1H OCEAN']
#['NEAR BAY']]
#print(type(X)) #
n_samples, n_features = X.shape
#print(X.shape) #(16512, 1)
#the prefix underscore: private variable,
#the trailing underscore is used by convention to avoid naming conflicts
self._label_encoders_ = [LabelEncoder() for _ in range(n_features)] #[LabelEncoder,...]
for i in range(n_features):
le = self._label_encoders_[i]
Xi = X[:, i]
if self.categories == 'auto':
le.fit(Xi)
else:
#np.in1d(ar1,ar2): Returns a boolean array the same length as ar1 that
#is True where an element of ar1 is in ar2
#and False otherwise.
valid_mask = np.in1d(Xi, self.categories[i])
if not np.all(valid_mask):
if self.handle_unknown == 'error':
diff = np.unique(Xi[~valid_mask])
msg = ("Found unknown categories {0} in column {1} during fit".format(diff, i))
raise ValueError(msg)
le.classes_ = np.array(np.sort(self.categories[i]))
#for examples,here is ['<1H OCEAN' 'INLAND' 'ISLAND' 'NEAR BAY' 'NEAR OCEAN']
#encoder.classes_
self.categories_ = [le.classes_ for le in self._label_encoders_]
return self
def transform(self, X):
"""Transform X using one-hot encoding.
Parameters
----------
X : array-like, shape [n_samples, n_features]
The data to encode.
Returns
-------
X_out : sparse matrix or a 2-d array
Transformed input.
"""
#check_array: By default, the input(here is X) is converted to an at least 2D numpy array.
#If the dtype of the array is object, attempt converting to float, raising on failure.
#csc_matrix: https://docs.scipy.org/doc/scipy/reference/generated/scipy.sparse.csc_matrix.html
X = check_array(X, accept_sparse='csc', dtype=np.object, copy=True)
n_samples, n_features = X.shape
X_int = np.zeros_like(X, dtype=np.int)
X_mask = np.ones_like(X, dtype=np.bool) #dtype:Overrides the data type of the result
#conver the 1s to all True
for i in range(n_features):
#Returns a boolean array the same length as ar1 that is True where an element of ar1 is in ar2
#and False otherwise.
valid_mask = np.in1d(X[:, i], self.categories_[i]) #[ True True True ... True True True]
if not np.all(valid_mask):
if self.handle_unknown == 'error':
diff = np.unique(X[~valid_mask, i])
msg = ("Found unknown categories {0} in column {1} during transform".format(diff, i))
raise ValueError(msg)
else:
# Set the problematic rows to an acceptable value and
# continue `The rows are marked `X_mask` and will be
# removed later.
X_mask[:, i] = valid_mask
X[:, i][~valid_mask] = self.categories_[i][0]
X_int[:, i] = self._label_encoders_[i].transform(X[:, i]) #[0 0 4 ... 1 0 3]
if self.encoding == 'ordinal':
return X_int.astype(self.dtype, copy=False)
mask = X_mask.ravel() #[ True True True ... True True True]
#self.categories_: [array(['<1H OCEAN', 'INLAND', 'ISLAND', 'NEAR BAY', 'NEAR OCEAN'], dtype=object)]
#cats.shape[0] ==5
n_values = [cats.shape[0] for cats in self.categories_] #self.categories_ :2D numpy array
n_values = np.array([0] + n_values) #[[0] [5]]
indices = np.cumsum(n_values) #[0 5]
column_indices = (X_int + indices[:-1]).ravel()[mask] #extraction:[0 0 4 ... 1 0 3]
row_indices = np.repeat(np.arange(n_samples, dtype=np.int32),n_features)[mask]
data = np.ones(n_samples * n_features)[mask]
out = sparse.csc_matrix((data, (row_indices, column_indices)),
shape=(n_samples, indices[-1]),
dtype=self.dtype
).tocsr()
if self.encoding == 'onehot-dense':
return out.toarray()
else:
return out from sklearn.pipeline import Pipeline
from sklearn.linear_model import LinearRegression
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.preprocessing import Imputer
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import FeatureUnion #Sckit-learn <0.20
class DataFrameSelector(BaseEstimator, TransformerMixin):
def __init__(self, attribute_names):
self.attribute_names = attribute_names
def fit(self, X, y=None):
return self
def transform(self, X):
return X[self.attribute_names].values
class CombinedAttributesAdder(BaseEstimator, TransformerMixin):
def __init__(self, add_bedrooms_per_room = True): #no *args or **kargs
self.add_bedrooms_per_room = add_bedrooms_per_room
def fit(self, X, y=None):
return self #nothing else to do
def transform(self, X, y=None):
rooms_per_household = X[:, rooms_ix] / X[:, household_ix]
population_per_household = X[:, population_ix] / X[:, household_ix]
if self.add_bedrooms_per_room:
bedrooms_per_room = X[:, bedrooms_ix] / X[:,rooms_ix]
#Translates slice objects to concatenation along the second axis.
return np.c_[X, rooms_per_household, population_per_household, bedrooms_per_room]
else:
return np.c_[X, rooms_per_household, population_per_household]
num_pipeline=Pipeline([
('selector', DataFrameSelector(num_attribs)),
('imputer', Imputer(strategy='median')),
('attribs_adder', CombinedAttributesAdder()),
('std_scaler', StandardScaler()),
])
cat_pipeline = Pipeline([
('selector', DataFrameSelector(cat_attribs)), #
('label_binarizer',CategoricalEncoder(encoding="onehot-dense")) #CategoricalEncoder(encoding="onehot-dense")
])
full_pipeline = FeatureUnion(n_jobs=1, #default 1
transformer_list=[('num_pipeline', num_pipeline),
('cat_pipeline', cat_pipeline),
]
)
full_pipeline_with_predictor = Pipeline([
("preparation", full_pipeline),
("linear", LinearRegression())
])
full_pipeline_with_predictor.fit(housing, housing_label)
some_data = housing.iloc[:5]
full_pipeline_with_predictor.predict(some_data)You should save every model you experiment with, so you can come back easily to any model you want. Make sure you save both the hyperparameters and the trained parameters, as well as the cross-validation scores and perhaps the actual predictions as well. This will allow you to easily compare scores across model types, and compare the types of errors they make. You can easily save Scikit-Learn models by using Python’s pickle module, or using sklearn.externals.joblib, which is more efficient at serializing large NumPy arrays:
Model persistence using joblib
my_model = full_pipeline_with_predictor
import joblib
joblib.dump(my_model, "my_model.pkl") #DIFF
#...
my_model_loaded = joblib.load("my_model.pkl") #DIFF
my_model_loaded
Example SciPy distributions for RandomizedSearchCV
https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.geom.html
from scipy.stats import geom, expon
#A geometric discrete random variable.
# rvs: Random variates of given type.
geom_distrib = geom(0.5).rvs(10000, random_state=42)
expon_distrib = expon(scale=1).rvs(10000, random_state=42)
plt.hist(geom_distrib, bins=50)
plt.show()
plt.hist(expon_distrib, bins=50)
plt.show()
Exercise solution
Using this chapter’s housing dataset:
1. Try a Support Vector Machine regressor (sklearn.svm.SVR), with various hyperparameters such as kernel="linear" (with various values for the C hyperparameter) or kernel="rbf" (with various values for the C and gamma hyperparameters). Don’t worry about what these hyperparameters mean for now. How does the best SVR predictor perform?
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVR
param_grid = [
{'kernel': ['linear'], 'C':[10., 30., 100., 300., 1000., 3000., 10000., 30000.0] },
{'kernel': ['rbf'], 'C':[1.0, 3.0, 10., 30., 100., 300., 1000.0],'gamma': [0.01, 0.03, 0.1, 0.3, 1.0, 3.0] },
] # 1*8 + 1*7*6=50
svm_reg = SVR()
grid_search = GridSearchCV(svm_reg, param_grid, cv=5, scoring="neg_mean_squared_error", verbose=2)
grid_search.fit(housing_prepared, housing_label)The best model achieves the following score (evaluated using 5-fold cross validation):
negative_mse = grid_search.best_score_
rmse = np.sqrt(-negative_mse)
rmse![]()
That's much worse than the RandomForestRegressor(50010.477372130474 {'max_features': 6, 'n_estimators': 30}) .Let's check the best hyperparameters found:
grid_search.best_params_![]()
The linear kernel seems better than the RBF kernel. Notice that the value of C is the maximum tested value. When this happens you definitely want to launch the grid search again with higher values for C (removing the smallest values), because it is likely that higher values of C will be better.
2. Try replacing GridSearchCV with RandomizedSearchCV.
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import expon, reciprocal
param_distribs = {
'kernel': ['linear', 'rbf'],
'C': reciprocal(150000, 160000),
'gamma': expon(scale=1.0)
}
svm_reg = SVR()
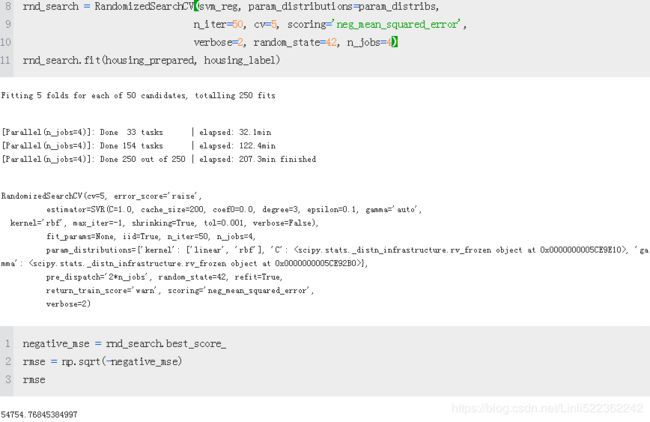
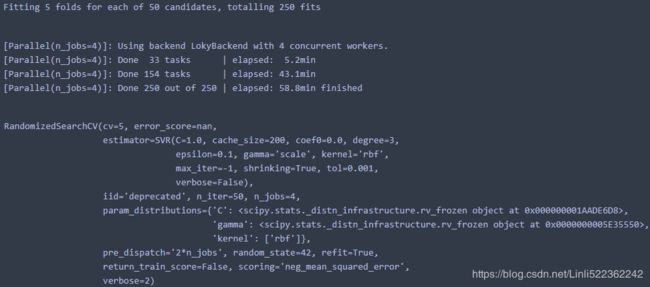
rnd_search = RandomizedSearchCV(svm_reg, param_distributions=param_distribs,
n_iter=50, cv=5, scoring='neg_mean_squared_error',
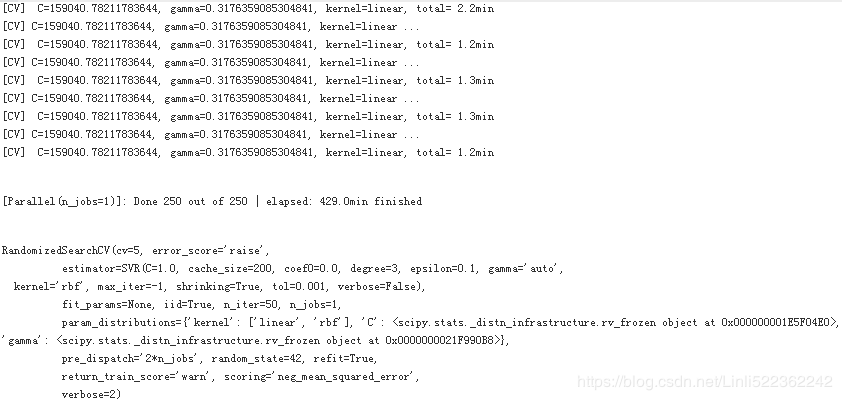
verbose=2, random_state=42)
rnd_search.fit(housing_prepared, housing_label)In the second run, I set the n_jobs =4 instead using default value 1,
The best model achieves the following score (evaluated using 5-fold cross validation):
negative_mse = rnd_search.best_score_
rmse = np.sqrt(-negative_mse)
rmse![]()
Now this is much closer to the performance of the RandomForestRegressor (but not quite there yet, 50010.477372130474 {'max_features': 6, 'n_estimators': 30} ). Let's check the best hyperparameters found:
rnd_search.best_params_![]()
This time the search found a good set of hyperparameters for the RBF kernel. Randomized search tends to find better hyperparameters than grid search in the same amount of time. (grid search ![]() , need more trials since 'C' has been limited to 30000)
, need more trials since 'C' has been limited to 30000)
Let's look at the exponential distribution we used, with scale=1.0. Note that some samples are much larger(>1000) or smaller than 1.0, but when you look at the log of the distribution, you can see that most values are actually concentrated roughly in the range of exp(-2) to exp(+2), which is about 0.1 to 7.4. Note(log e^x = x)
(Randomized search tends to find better hyperparameters![]() )
)
Our C and gamma are sampled using a reciprocal distribution and an exponential distribution, respectively.
Analog sampling process
expon_distrib = expon(scale=1.) # scale=1/lambda
#Generate random numbers
samples = expon_distrib.rvs(10000, random_state=42)
plt.figure(figsize=(10, 4))
plt.subplot(121)
plt.title("Exponential distribution (scale=1.0)")
plt.hist(samples, bins=50)#bins: groups
plt.subplot(122)
plt.title("Log of this distribution")
plt.hist(np.log(samples), bins=50)
plt.show()
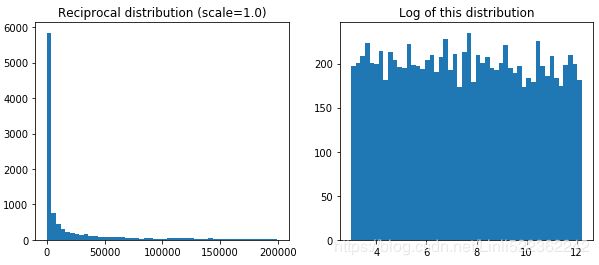
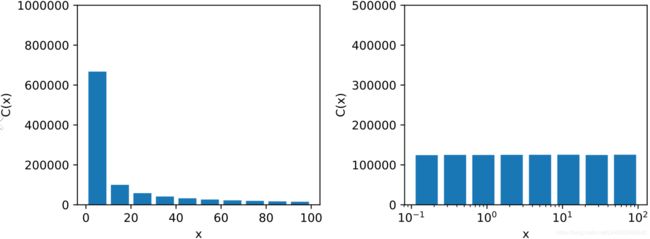
The distribution we used for C looks quite different: the scale of the samples is picked from a uniform distribution within a given range从给定范围内的均匀分布中选取样本的比例(eg.I set reciprocal(150000, 160000)), which is why the right graph, which represents the log of the samples, looks roughly constant. This distribution is useful when you don't have a clue of what the target scale目标比例 is:
reciprocal_distrib = reciprocal(20, 200000) #the previous code, I set reciprocal(150000, 160000) #log-uniform distribution
samples = reciprocal_distrib.rvs(10000, random_state=42)
plt.figure(figsize=(10, 4))
plt.subplot(121)
plt.title("Reciprocal distribution (scale=1.0)")
plt.hist(samples, bins=50)
plt.subplot(122)
plt.title("Log of this distribution")
plt.hist(np.log(samples), bins=50)
plt.show()The reciprocal distribution is useful when you have no idea what the scale范围大小 of the hyperparameter should be (indeed, as you can see on the figure on the right, all scales are equally likely, within the given range), whereas the exponential distribution is best when you know (more or less) what the scale of the hyperparameter should be(集中左侧).
#################
In probability and statistics, the reciprocal distribution, also known as the log-uniform distribution, is a continuous probability distribution. It is characterised by its probability density function, within the support of the distribution, being proportional to the reciprocal of the variable.
The reciprocal distribution is an example of an inverse distribution, and the reciprocal (inverse) of a random variable with a reciprocal distribution itself has a reciprocal distribution.
A positive random variable X is log-uniformally distributed if the logarithm of X is uniform distributed,
![]()
https://en.wikipedia.org/wiki/Reciprocal_distribution
#################
3. Try adding a transformer in the preparation pipeline to select only the most important attributes.
#########
#To obtain the k-largest values use
import numpy as np
#0 1 2 3 4 5 6 7
A = np.array([1, 7, 9, 2, 0.1, 17, 17, 1.5])
k = 3
idx = np.argpartition(A, -k) #(hiding: sort)
# [4 0 7 3 1 2 6 5]
A[idx[-k:]]
# [ 9. 17. 17.]from sklearn.base import BaseEstimator, TransformerMixin
def indices_of_top_k(arr, k):
#argpartition(a, kth, axis=-1, kind='introselect', order=None):
#Perform an indirect partition along the given axis using the
#algorithm (specified by the `kind` keyword). It returns an array of
#indices of the same shape as `a` that index data along the given
#axis in partitioned order.
return np.sort(np.argpartition( np.array(arr), -k )[-k:]) #best to use both negative k
class TopFeaturesSelector(BaseEstimator, TransformerMixin):
def __init__(self, feature_importances, k):
self.feature_importances = feature_importances
self.k =k
def fit(self, X, y=None):
self.feature_indices_ = indices_of_top_k(self.feature_importances, self.k)
return self
def transform(self, X):
return X[:, self.feature_indices_]Note: this feature selector assumes that you have already computed the feature importances somehow (for example using a RandomForestRegressor). You may be tempted to compute them directly in the TopFeatureSelector's fit() method, however this would likely slow down grid/randomized search since the feature importances would have to be computed for every hyperparameter combination (unless you implement some sort of cache).
Let's define the number of top features we want to keep:
k=5Now let's look for the indices of the top k features:
top_k_feature_indices = indices_of_top_k(feature_importances, k)
top_k_feature_indicesnp.array(attributes)[top_k_feature_indices]![]()
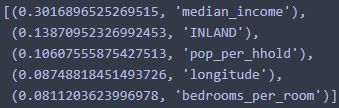
Let's double check that these are indeed the top k features:
sorted(zip(feature_importances, attributes), reverse=True)[:k]Looking good... Now let's create a new pipeline that runs the previously defined preparation pipeline, and adds top k feature selection: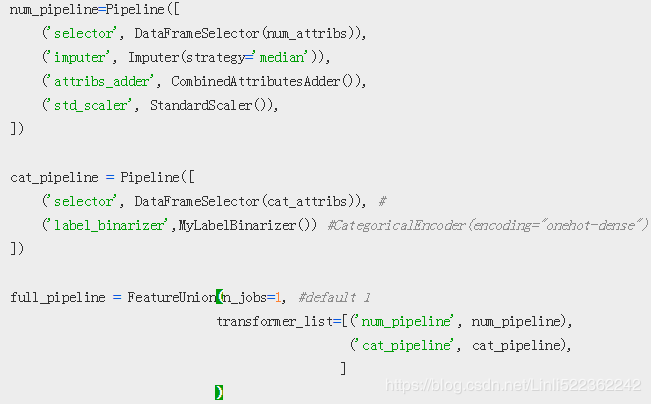
preparation_and_feature_selection_pipeline = Pipeline([
("preparation", full_pipeline),
("feature_slection", TopFeaturesSelector(feature_importances, k))
])
housing_prepared_top_k_features = preparation_and_feature_selection_pipeline.fit_transform(housing)housing_prepared_top_k_features[:3] #3: first 3 rows or first 3 instances
housing_prepared[:3, top_k_feature_indices] #k=5; #3: first 3 rows or first 3 instances
4. Try creating a single pipeline that does the full data preparation plus the final prediction.
prepare_select_and_predict_pipeline = Pipeline([
('preparation', full_pipeline),
('feature_selection', TopFeaturesSelector(feature_importances, k)), #k=5
('svm_reg', SVR(**rnd_search.best_params_))
#{'C': 159729.22458141073, 'gamma': 0.26497040005002437, 'kernel': 'rbf'}
])
prepare_select_and_predict_pipeline.fit(housing, housing_label)
some_data = housing.iloc[:4]
some_labels = housing_label.iloc[:4]
print("Predictions:\t", prepare_select_and_predict_pipeline.predict(some_data))
print("Labels:\t\t", list(some_labels))![]()
Well, the full pipeline seems to work fine. Of course, the predictions are not fantastic: they would be better if we used the best RandomForestRegressor that we found earlier, rather than the best SVR.
5. Automatically explore some preparation options using GridSearchCV.
#Wrong:rnd_search..best_estimator_.feature_importance#RandomizedSearchCV has not feature_importance
https://repl.it/@LIQINGLIN54951/BoilingFixedTabs-1
#pip install jupyter_contrib_nbextensions && jupyter contrib nbextension install
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.model_selection import GridSearchCV
from sklearn.pipeline import Pipeline
try:
from sklearn.preprocessing import Imputer
except:
from sklearn.impute import SimpleImputer as Imputer
from sklearn.model_selection import StratifiedShuffleSplit
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import FeatureUnion #Sckit-learn <0.20
import numpy as np
import pandas as pd
from sklearn.svm import SVR
from scipy.stats import expon, reciprocal
from sklearn.model_selection import RandomizedSearchCV
from sklearn.ensemble import RandomForestRegressor
#######################get data###############
def load_housing_data():
csv_path='https://raw.githubusercontent.com/ageron/handson-ml/master/datasets/housing/housing.csv'
return pd.read_csv(csv_path) #returns a Pandas DataFrame object containing all the data
housing = load_housing_data()
housing['income_cat'] = np.ceil(housing['median_income']/1.5)
housing['income_cat'].where(housing['income_cat']<5, 5.0, inplace=True)
housing['income_cat'].head()
#######################get strat_train_set and strat_test_set###############
#n_splits: n groups of train/test pair
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42) #one group of train/test pair
for train_index, test_index in split.split(housing, housing['income_cat']):
strat_train_set = housing.loc[train_index]
strat_test_set = housing.loc[test_index]
#remove the income_cat attribute so the data is back to its original state:
for set in (strat_train_set, strat_test_set):
set.drop(["income_cat"], axis=1, inplace=True)
#get a training set and a label set
housing = strat_train_set.drop('median_house_value', axis=1) #return a dataframe without the dropped column
housing_label = strat_train_set["median_house_value"].copy()
#########################CategoricalEncoder Class########################
from sklearn.utils import check_array
from sklearn.preprocessing import LabelEncoder
from scipy import sparse
class CategoricalEncoder(BaseEstimator, TransformerMixin):
def __init__(self, encoding='onehot', categories='auto', dtype=np.float64, handle_unknown='error'):
self.encoding = encoding
self.categories = categories
self.dtype = dtype
self.handle_unknown = handle_unknown
def fit(self, X, y=None):
"""Fit the CategoricalEncoder to X.
Parameters
----------
X : array-like, shape [n_samples, n_feature]
The data to determine the categories of each feature.
Returns
-------
self
"""
if self.encoding not in ['onehot', 'onehot-dense', 'ordinal']:
template = ("encoding should be either 'onehot', 'onehot-dense' or 'ordinal', got %s")
raise ValueError(template % self.handle_unknown)
if self.handle_unknown not in ['error', 'ignore']:
template = ("handle_unknown should be either 'error' or 'ignore', got %s")
raise ValueError(template % self.handle_unknown)
if self.encoding == 'ordinal' and self.handle_unknown == 'ignore':
raise ValueError("handle_unknown='ignore' is not supported for encoding='ordinal'")
#check_array: By default, the input(here is X) is converted to an at least 2D numpy array.
#If the dtype of the array is object, attempt converting to float, raising on failure.
#csc_matrix: https://docs.scipy.org/doc/scipy/reference/generated/scipy.sparse.csc_matrix.html
X = check_array(X, dtype=np.object, accept_sparse='csc', copy=True)
#print(X)
#[['<1H OCEAN']
#['<1H OCEAN']
#['NEAR OCEAN']
#...
#['INLAND']
#['<1H OCEAN']
#['NEAR BAY']]
#print(type(X)) #
n_samples, n_features = X.shape
#print(X.shape) #(16512, 1)
#the prefix underscore: private variable,
#the trailing underscore is used by convention to avoid naming conflicts
self._label_encoders_ = [LabelEncoder() for _ in range(n_features)] #[LabelEncoder,...]
for i in range(n_features):
le = self._label_encoders_[i]
Xi = X[:, i]
if self.categories == 'auto':
le.fit(Xi)
else:
#np.in1d(ar1,ar2): Returns a boolean array the same length as ar1 that
#is True where an element of ar1 is in ar2
#and False otherwise.
valid_mask = np.in1d(Xi, self.categories[i])
if not np.all(valid_mask):
if self.handle_unknown == 'error':
diff = np.unique(Xi[~valid_mask])
msg = ("Found unknown categories {0} in column {1} during fit".format(diff, i))
raise ValueError(msg)
le.classes_ = np.array(np.sort(self.categories[i]))
#for examples,here is ['<1H OCEAN' 'INLAND' 'ISLAND' 'NEAR BAY' 'NEAR OCEAN']
#encoder.classes_
self.categories_ = [le.classes_ for le in self._label_encoders_]
return self
def transform(self, X):
"""Transform X using one-hot encoding.
Parameters
----------
X : array-like, shape [n_samples, n_features]
The data to encode.
Returns
-------
X_out : sparse matrix or a 2-d array
Transformed input.
"""
#check_array: By default, the input(here is X) is converted to an at least 2D numpy array.
#If the dtype of the array is object, attempt converting to float, raising on failure.
#csc_matrix: https://docs.scipy.org/doc/scipy/reference/generated/scipy.sparse.csc_matrix.html
X = check_array(X, accept_sparse='csc', dtype=np.object, copy=True)
n_samples, n_features = X.shape
X_int = np.zeros_like(X, dtype=np.int)
X_mask = np.ones_like(X, dtype=np.bool) #dtype:Overrides the data type of the result
#conver the 1s to all True
for i in range(n_features):
#Returns a boolean array the same length as ar1 that is True where an element of ar1 is in ar2
#and False otherwise.
valid_mask = np.in1d(X[:, i], self.categories_[i]) #[ True True True ... True True True]
if not np.all(valid_mask):
if self.handle_unknown == 'error':
diff = np.unique(X[~valid_mask, i])
msg = ("Found unknown categories {0} in column {1} during transform".format(diff, i))
raise ValueError(msg)
else:
# Set the problematic rows to an acceptable value and
# continue `The rows are marked `X_mask` and will be
# removed later.
X_mask[:, i] = valid_mask
X[:, i][~valid_mask] = self.categories_[i][0]
X_int[:, i] = self._label_encoders_[i].transform(X[:, i]) #[0 0 4 ... 1 0 3]
if self.encoding == 'ordinal':
return X_int.astype(self.dtype, copy=False)
mask = X_mask.ravel() #[ True True True ... True True True]
#self.categories_: [array(['<1H OCEAN', 'INLAND', 'ISLAND', 'NEAR BAY', 'NEAR OCEAN'], dtype=object)]
#cats.shape[0] ==5
n_values = [cats.shape[0] for cats in self.categories_] #self.categories_ :2D numpy array
n_values = np.array([0] + n_values) #[[0] [5]]
indices = np.cumsum(n_values) #[0 5]
column_indices = (X_int + indices[:-1]).ravel()[mask] #extraction:[0 0 4 ... 1 0 3]
row_indices = np.repeat(np.arange(n_samples, dtype=np.int32),n_features)[mask]
data = np.ones(n_samples * n_features)[mask]
out = sparse.csc_matrix((data, (row_indices, column_indices)),
shape=(n_samples, indices[-1]),
dtype=self.dtype
).tocsr()
if self.encoding == 'onehot-dense':
return out.toarray()
else:
return out
########### CombinedAttributesAdder Class################
rooms_ix, bedrooms_ix, population_ix, household_ix = 3,4,5,6
class CombinedAttributesAdder(BaseEstimator, TransformerMixin):
def __init__(self, add_bedrooms_per_room = True): #no *args or **kargs
self.add_bedrooms_per_room = add_bedrooms_per_room
def fit(self, X, y=None):
return self #nothing else to do
def transform(self, X, y=None):
rooms_per_household = X[:, rooms_ix] / X[:, household_ix]
population_per_household = X[:, population_ix] / X[:, household_ix]
if self.add_bedrooms_per_room:
bedrooms_per_room = X[:, bedrooms_ix] / X[:,rooms_ix]
#Translates slice objects to concatenation along the second axis.
return np.c_[X, rooms_per_household, population_per_household, bedrooms_per_room]
else:
return np.c_[X, rooms_per_household, population_per_household]
#################DataFrameSelector##################
class DataFrameSelector(BaseEstimator, TransformerMixin):
def __init__(self, attribute_names):
self.attribute_names = attribute_names
def fit(self, X, y=None):
return self
def transform(self, X):
return X[self.attribute_names].values
#Handling Text and Categorical Attributes
housing_num = housing.drop('ocean_proximity', axis=1)#return a dataframe without the dropped column
num_attribs = list(housing_num)
#housing_cat = housing['ocean_proximity']
cat_attribs = ["ocean_proximity"]
num_pipeline = Pipeline([
('imputer', Imputer(strategy="median")),#fill missing value with median of each attribute
('attribs_adder', CombinedAttributesAdder()),
('std_scaler', StandardScaler()),
])
full_pipeline = ColumnTransformer([#must use it for Question5
("num", num_pipeline, num_attribs),
("cat", CategoricalEncoder(encoding="onehot-dense"), cat_attribs),
])
housing_prepared = full_pipeline.fit_transform(housing)
####################RandomizedSearchCV(SVR()) to get rnd_search.best_params_##################
param_distribs = {
'kernel': ['rbf'],# 'linear',
'C': reciprocal(20, 200000),
'gamma': expon(scale=1.0)
}
svm_reg = SVR()
rnd_search = RandomizedSearchCV(svm_reg, param_distributions=param_distribs,
n_iter=50, cv=5, scoring='neg_mean_squared_error',
verbose=2, random_state=42, n_jobs=4) #Back end(Jupyter Note CMD)
rnd_search.fit(housing_prepared, housing_label) rnd_search.best_params_
#############using RandomForestRegressor() to get feature_importances####################
#All in all, the grid search will explore 12 + 6 = 18 combinations of RandomForestRegressor hyperparameter values,
param_grid = [
#This param_grid tells Scikit-Learn to first evaluate all 3 × 4 = 12
#combinations of n_estimators and max_features hyperparameter values specified in the first dict
{'n_estimators': [30], 'max_features':[6,8]}, #{'n_estimators': [3,10,30], 'max_features':[2,4,6,8]},
#then try all 2 × 3 = 6 combinations of hyperparameter values in the second dict,
#but this time with the bootstrap hyperparameter set to False instead of
#True (which is the default value for this hyperparameter).
{'bootstrap': [False], 'n_estimators':[3,10], 'max_features':[2,3,4]}
]
forest_reg = RandomForestRegressor()
#it will train each model five times (since we are using five-fold cross validation).
#In other words, all in all, there will be 18 × 5 = 90 rounds of training!
grid_search = GridSearchCV(forest_reg, param_grid, cv=5, scoring='neg_mean_squared_error', n_jobs=1)
grid_search.fit(housing_prepared, housing_label)
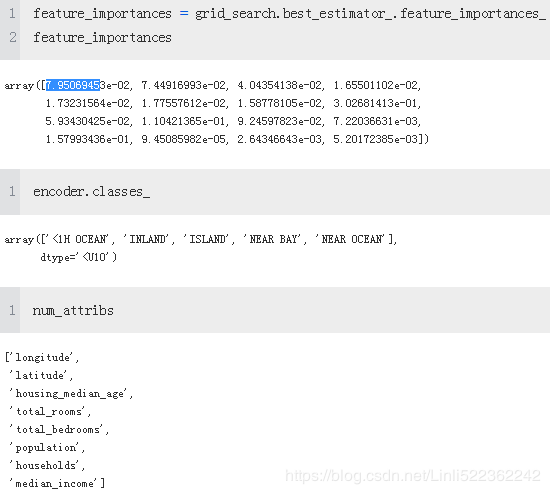
feature_importances =grid_search.best_estimator_.feature_importances_# array([7.01701239e-02, 6.52663337e-02, 4.31032563e-02, 1.50706903e-02,
# 1.43336241e-02, 1.53893508e-02, 1.34375275e-02, 3.52588696e-01,
# 5.20418545e-02, 1.14332160e-01, 7.30729044e-02, 5.54690944e-03,
# 1.61111457e-01, 4.52779559e-05, 1.84552331e-03, 2.64431065e-03])
feature_importances
####################RandomizedSearchCV(SVR()) to get rnd_search.best_params_##################
param_distribs = {
'kernel': ['rbf'],# 'linear',
'C': reciprocal(20, 200000),
'gamma': expon(scale=1.0)
}
svm_reg = SVR()
rnd_search = RandomizedSearchCV(svm_reg, param_distributions=param_distribs,
n_iter=50, cv=5, scoring='neg_mean_squared_error',
verbose=2, random_state=42, n_jobs=4) #Back end(Jupyter Note CMD)
rnd_search.fit(housing_prepared, housing_label)##################TopFeatureSelector###############
def indices_of_top_k(arr, k):
#argpartition(a, kth, axis=-1, kind='introselect', order=None):
#Perform an indirect partition along the given axis using the
#algorithm (specified by the `kind` keyword). It returns an array of
#indices of the same shape as `a` that index data along the given
#axis in partitioned order.
return np.sort(np.argpartition( np.array(arr), -k )[-k:]) #best to use both negative k
class TopFeatureSelector(BaseEstimator, TransformerMixin):
def __init__(self, feature_importances, k):
self.feature_importances = feature_importances
self.k = k
def fit(self, X, y=None):
self.feature_indices_ = indices_of_top_k(self.feature_importances, self.k)
return self
def transform(self, X):
return X[:, self.feature_indices_]
k=5
top_k_feature_indices = indices_of_top_k(feature_importances, k)
top_k_feature_indices ![]()
extra_attribs = ["rooms_per_hhold", "pop_per_hhold", "bedrooms_per_room"]
#cat_encoder = cat_pipeline.named_steps["cat_encoder"] # old solution
cat_encoder = full_pipeline.named_transformers_["cat"]
cat_one_hot_attribs = list(cat_encoder.categories_[0])
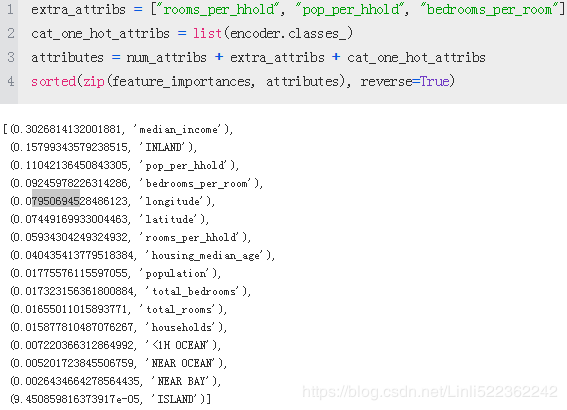
attributes = num_attribs + extra_attribs + cat_one_hot_attribs
sorted(zip(feature_importances, attributes), reverse=True)[:k]prepare_select_and_predict_pipeline = Pipeline([
('preparation', full_pipeline),
('feature_selection', TopFeatureSelector(feature_importances, k)), #k=5
('svm_reg', SVR(**rnd_search.best_params_))
#{'C': 159729.22458141073, 'gamma': 0.26497040005002437, 'kernel': 'rbf'}
])
param_grid = [{
'preparation__num__imputer__strategy': [ 'mean', 'median', 'most_frequent'],
'feature_selection__k': list(range(14, len(feature_importances) + 1))
}]
grid_search_prep = GridSearchCV(prepare_select_and_predict_pipeline, param_grid, cv=5,
scoring='neg_mean_squared_error', verbose=2, n_jobs=2)
grid_search_prep.fit(housing, housing_label)
print( grid_search_prep.best_params_ ) The best imputer strategy is most_frequent and apparently almost all features are useful (15 out of 16). The last one (ISLAND) seems to just add some noise.