洛谷P1004方格取数（Ｃ＋＋）

P1004方格取数

题目描述
设有N \times NN×N的方格图(N \le 9)(N≤9)，我们将其中的某些方格中填入正整数，而其他的方格中则放入数字00。如下图所示（见样例）:

A
 0  0  0  0  0  0  0  0
 0  0 13  0  0  6  0  0
 0  0  0  0  7  0  0  0
 0  0  0 14  0  0  0  0
 0 21  0  0  0  4  0  0
 0  0 15  0  0  0  0  0
 0 14  0  0  0  0  0  0
 0  0  0  0  0  0  0  0
                      　B

某人从图的左上角的AA点出发，可以向下行走，也可以向右走，直到到达右下角的BB点。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字00）。
此人从AA点到BB点共走两次，试找出22条这样的路径，使得取得的数之和为最大。

输入输出格式
输入格式：
输入的第一行为一个整数NN（表示N \times NN×N的方格图），接下来的每行有三个整数，前两个表示位置，第三个数为该位置上所放的数。一行单独的00表示输入结束。
输出格式：
只需输出一个整数，表示22条路径上取得的最大的和。

输入输出样例
输入样例#1： 复制
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
输出样例#1： 复制
67
说明
NOIP 2000 提高组第四题

题目简介（复杂的思路，蒟蒻的代码 ）
话说我好久没写题解了啊（仿佛上午才提交了一个，最近高产似母猪啊 ）。这波，我们先分析一下。

这道题，和P1006传纸条基本相似（如果没刷过洛谷P1006的童鞋，推荐你去刷一刷洛谷P1006传纸条）
废话不多说，我们继续讲题。

这是NOIP2000的提高组的第四题。这道题，蒟蒻的我一看都知道这是DP来做。没学DP的童鞋也不要慌，因为，这道题还可以用DFS（不剪枝洛谷对3个样例，蒟蒻不会剪枝，还是老老实实写DP吧~）（虽然题目的数据规模不大，n<=9，但是不会剪枝真的很尴尬）
[我们会有DP、DFS两种解题，但是我重点讲DP（主要是DFS不会剪枝 ） ]

我们觉得用DP会比较好

DP方法

思路
四维动规的模板题，好了，目测水题，题解结束··· ···
（不是，拿错剧本了[/划去]）

我们来捋一捋题目：
由题得：
要从A（1,1）到B（n，n）再返回A（1,1）走过的位置，数要被去掉，并且求走过的数累加的最大值[如图，即为所示]

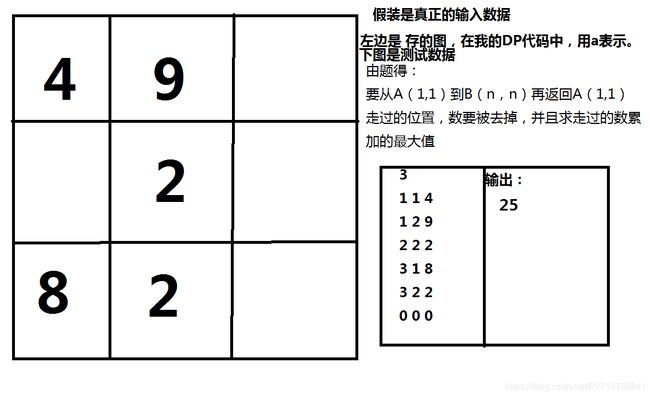
为了方便，我重新瞎编乱造了一个样例。
然后我们继续讲题。我们来看看，这个下图的走法（黑色为数组存图，红色为下标的提示，蓝色为位置提示，绿色为从A到B再回到A大致流程）。看完以后，我们来思考一个问题。

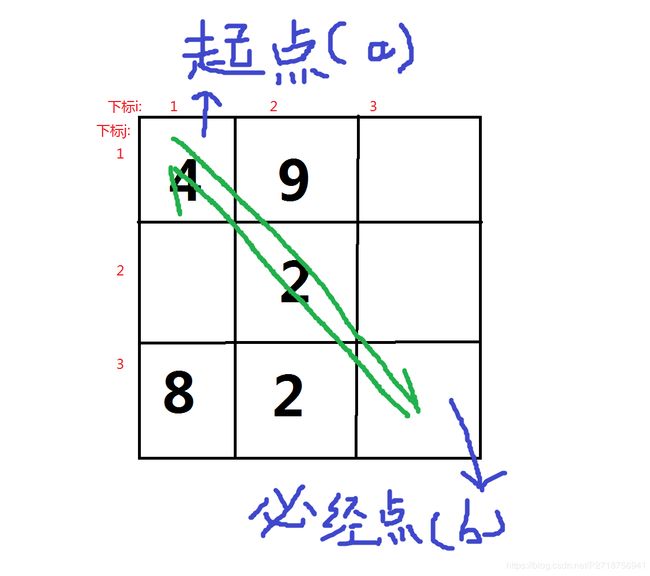
Q:这个地方应该怎么处理呢？DP貌似有点复杂啊！[汗]
答：其实这个地方很好办。That`s easy for we.这个嘛，我们假装看成两个人，他们都从A(1,1)走向B（n，n）。[如图]

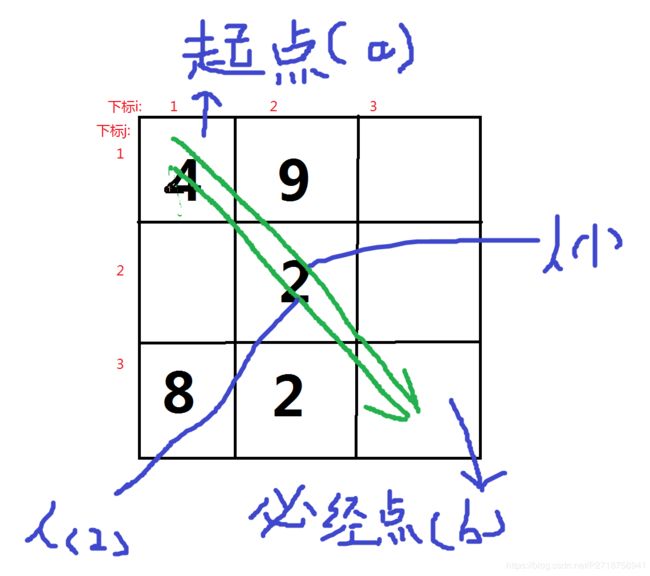
翻箱倒柜，终于想起一个叫做四维DP的东西，因为这题是两个人走，我们思考一下能不能单纯用两个人的模拟过呢？
显然是可以的，我们用 dp[i][j][k][l]表示第1条路线（第一个人）的（i，j）走法和第2条路线(第二个人）的（k，l）走法。
显然我们可以两个人一起走（我们手牵手，我们一起走 ），复杂度是N的4次方（笑喷，时间复杂度这么低）
所以我们就用这个方法了！
(没意见1次，没意见2次，成交！）

好，思路有了，就差代码了。
诶，别慌，我们还有东西没讲：f[i][j][k][l]=max(f[i-1][j][k-1][l],f[i][j-1][k-1][l],f[i-1][j][k][l-1],f[i][j-1][k][l-1])+a[i][j]+a[k][l];
对，就是万年公式

代码（接下来，就是最激动人心的代码公开环节了）

for(int i=1;i<=n;i++){//我居然公开了核心代码？？这很不兔子？
        for(int j=1;j<=n;j++){
            for(int k=1;k<=n;k++){
                for(int l=1;l<=n;l++){
                	
                    dp[i][j][k][l]=max(max(dp[i-1][j][k-1][l],dp[i-1][j][k][l-1]),max(dp[i][j-1][k-1][l],dp[i][j-1][k][l-1]))+a[i][j]+a[k][l];
                    
					if(i==k&&l==j)dp[i][j][k][l]-=a[i][j];
                    
                }
            }
        }
    }

继续，我们解释一下，这是四层循环嵌套（数据不会超时），里面就是这样的，不过多解释~

AC代码（老板，上代码！）

DFS部分

_{我的DFS和老师的差不多，我的太乱了，于是就粘了一段老师的未剪枝的代码}

TLE代码（不会剪枝，不解释）_{（感谢老师的源码提供}）~

本期题解就这样草率结束了，撒个小花花~
希望小伙伴们点个关注，下期我们再会，233333333~拜啦！！