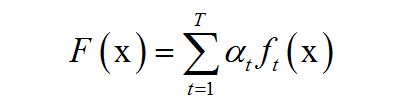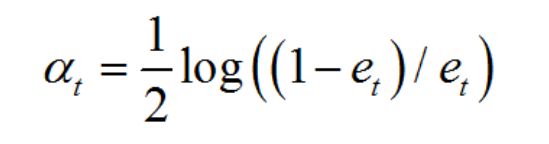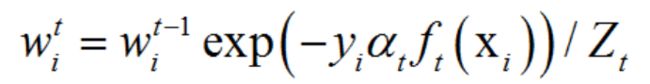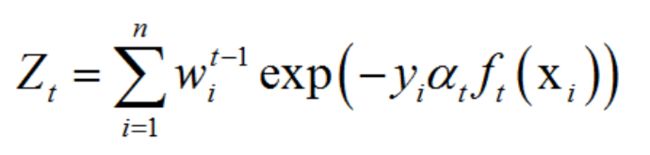Haar+adaboost人脸识别
前言
人脸识别的算法总的可以分为两步,首先是特征提取的部分,然后是根据特征进行判断;
01 首先我们来看一下特征提取的部分
图像的特征包含有图像的颜色特征、纹理特征、形状特征和空间关系特征。
在算法中,特征就是某个区域的像素点经过某种四则运算后所得到的结果。这种结果可以是一个具体的值,可以是一个向量,
可以是一个矩阵亦或是一个多维的数组。
所以说,特征的本质其实就是像素运算的结果。
02 判别部分
假设我们已经通过某种方法得到了我们所需要的特征,那么接下来要做的就是利用这些特征来区分目标了。
这里我们采用阈值判决法,即如果这个特征的取值大于某个特定的阈值,那么我们便认为他属于这个目标。
我们如何得到这个特定的阈值呢?总不能都以0.5为界吧?
这就要借助到我们的机器学习部分的方法了,我们通过使用机器学习的算法来得到这个判决阈值。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
这里我们要用到的特征是haar特征,那我们就来看一下什么是haar特征
Haar特征最先由Paul Viola等提出,后经过RainerLienhart等扩展引入45°倾斜特征,成为现在OpenCV所使用的的样子。
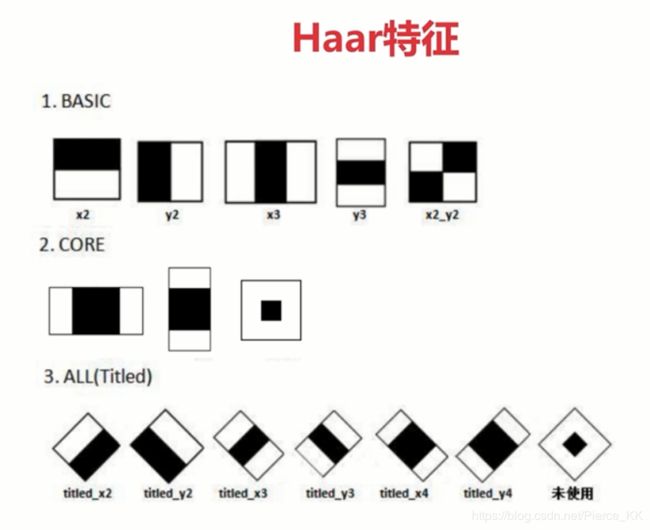
下图展示了目前OpenCV(2.4.11版本)所使用的共计14种Haar特征,包括5种Basic特征、3种Core特征和6种Titled(即45°旋转)特征。
拓展类型的原理与基本类型相同,只是在角度上或者是形状上稍有区别。
从图中可以看出,haar特征其实就是一些矩形区域,
在后续会对其进行放大的操作,但是同一个类型的矩形区域不管放大多少,其黑白面积比都不变。
Haar特征值反映了图像的灰度变化情况。例如:脸部的一些特征能由矩形特征简单的描述,如:眼睛要比脸颊颜色要深,鼻梁两侧比鼻梁颜色要深,嘴巴比周围颜色要深等。但矩形特征只对一些简单的图形结构,如边缘、线段较敏感,所以只能描述特定走向(水平、垂直、对角)的结构。
ok,现在我们明白了什么是haar特征,下面我们就来看一下如何计算haar特征
我们结合前面对于特征的定义,即特征其实就是在某一个区域内对像素进行四则运算所产生的结果
上图就是haar特征的计算方法;前两个方法是相同的,第三个方法是使用积分运算来减少运算量。
这里我们仅仅只是计算了图像上一个小区域的haar特征,要计算整幅图像的特征,我们需是这个方框对整幅图像做一个遍历(采用滑框的方式,即窗口平移)。
遍历一次后,我们需要对这个滑框进行几次的缩放(说是缩放,其尺寸也可以增加),每改变一次后都需要再进行一次完整的遍历。
在检测窗口通过平移+放大可以产生一系列Haar特征,这些特征由于位置和大小不同,分类效果也各异;通过计算Haar特征的特征值,可以有将图像矩阵映射为1维特征值,有效实现了降维。
特征值的标准化
我们可以来做一个简单地运算,一个12*18大小的Haar特征计算出的特征值变化范围从-2000~+6000,跨度非常大。
这种跨度大的特性不利于量化评定特征值,所以需要进行“标准化”,压缩特征值范围。OpenCV采用如下方式“标准化”:
Haar特征的部分就说到这里,下面我们来看一下如何利用我们的haar特征。
集成学习简介
haar特征一般会与adaboost一同使用。
haar特征 + Adaboost是一个非常常见的组合,在人脸识别上取的非常大成功。
adaboost 属于机器学习中集成学习算法的一种。
这里我们首先来看一下什么是集成学习。
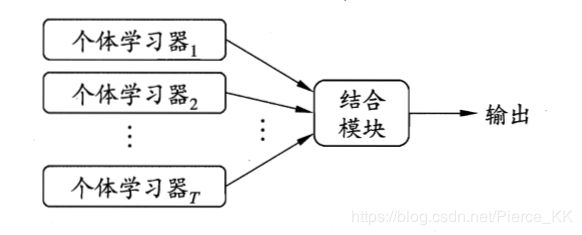
集成学习(ensemble)是通过构建并结合多个学习器来完成学习任务的。下图给出的是集成学习的一般结构,即先产生一组“个体学习器”,再由某种策略将他们结合起来。其中个体学习器通常由现有的学习算法从训练数据产生,例如c4.5决策树算法和BP神经网络算法等。
若集成中只包含同种类型的个体学习器(全是决策树或者全是BP),则称这样的集成为 “同质”, 相应的,同质集成中的个体学习器称之为 “ 基学习器 ”, 学习器所使用的算法则称之为“ 基学习算法 ”。
若集成中包含有不同类型的个体学习器,例如个体学习器1位决策树,个体学习器2为BP神经网络,我们则称这样的学习器为
“ 异质 ”的,这时也就不再有 “ 基学习器 ” 和“ 基学习算法 ”了,我们常称其为“ 组件学习器 ”,或直接称其为个体学习器。,
在集成学习中,要使集成后有好的效果,则我们的个体学习器应当“ 好而不同 ”,即个体学习器要有一定的准确性同时要有多样性 ,但是准确性与多样性似乎是一对矛盾的存在,因为在准确性得到提高的同时,势必会损失多样性。
根据个体学习器的生成方式,目前的集成学习大致可以分为两大类,
即个体学习器之间存在强依赖关系,必须串行生成的序列化方法;
以及个体学习器之间不存在强依赖关系,可以同时生成的并行化方法。
前者的代表是Boosting , 后者的代表是Bagging 和 “ 随机森林 ”(random forest)。
Boosting
Boosting的分类器由多个弱分类器组成,预测时用每个弱分类器分别进行预测,弱分类器是很简单的分类器,它计算量小且精度不用太高。 然后投票得到结果;(投票的方式如下)
这是可以将弱学习器提升为强学习器的算法,它的工作机制如下:
首先从训练样本中训练出一个基学习器, 再根据基学习器的标线对训练样本分布进行调整(调整的目的是使得先前基学习器判断错误的训练样本在此后可以受到更多的关注),然后使用调整后的数据集再来训练下一个基学习器。 如此反复进行,直到基学习器的数目达到了事先设定的值T, 最终将这T个基学习器进行加权结合。
adaboost 简介
我们此次使用的adaboost算法属于Boosting算法中的一个典型代表。
AdaBoost算法的全称是自适应Boosting(Adaptive Boosting),是一种二分类器,它用弱分类器的线性组合构造强分类器。
在基本的AdaBoost算法中,每个弱分类器都有权重,弱分类器预测结果的加权和形成了最终的预测结果。
(即adaboost是弱分类器的一个线性组合)
其中x是输入向量,F(x)是强分类器,ft(x)是弱分类器,αt是弱分类器的权重值,是一个正数,T为弱分类器的数量。弱分类器的输出值为+1或-1,分别对应于正样本和负样本。
分类时的判定规则为:
其中sgn( 有的书上也用sign )是符号函数。强分类器的输出值也为+1或-1,同样对应于正样本和负样本。
弱分类器和它们的权重值通过训练算法得到。之所以叫弱分类器是因为它们的精度不用太高。
adabost的训练
可以总结一下,adaboost在训练时的训练样本也有权重,在训练过程中动态调整,被前面的弱分类器错分类错误的样本会加大权重,因此算法会关注难分的样本。
弱分类器的权重值根据它的准确率构造,精度越高的弱分类器权重越大。 当然,弱分类器的权重越大,则其在投票是所占的比例也就越高。举个小例子来说明一下:
每个弱分类器类似于一个水平不太高的医生,如果在之前的考核中一个医生的技术更好,对病人情况的判断更准确,那么可以加大他在会诊时说话的分量即权重。而强分类器就是这些医生的结合。
下面我们来看一下算法的基本流程
01 初始化样本权重,使训练开始的时候所有样本拥有相同的权重。
02 做T次循环, 循环的目的是为了训练弱分类器,
03 对训练的一个弱分类器f(x),计算它对训练样本集的错误率e,
04 计算弱分类器的权重,公式如下: (强分类器是弱分类器的线性组合,所以当然要计算权重嘞。。)
(你可能会疑惑这个公式为什么是这个样子的,不要担心,你只需要先熟悉算法的流程并且知道有这个公式就好了,推导的部分可以看一下这里 https://www.itcodemonkey.com/article/8588.html。)
05 更新所有样本的权重, 公式如下: (前面说过了,adaboost需要对分类错误的样本赋予较大的权值)
其中Zt为归一化因子,它是所有样本的权重之和
06 全部的T的分类器训练完毕后结束循环,加权得到最终的强分类器。
给训练样本加权重是有必要的,如果样本没有权重,每个弱分类器的训练样本是相同的,训练出来的弱分类器也是一样的,这样训练多个弱分类器没有意义。
从算法的流程来看,每个个体学习器明显是串行生成的。生成的T个学习器之间都是有着很强的相关性的,应为任何一个学习器所使用的数据都是经由上一个学习器学习效果改正过的数据。 这是典型的集成学习中的Boosting
AdaBoost算法的原则是:
关注之前被错分的样本,准确率高的弱分类器有更大的权重。
上面的算法中并没有说明弱分类器是什么样的,具体实现时我们应该选择什么样的分类器作为弱分类器?
一般用深度很小的决策树。
强分类器是弱分类器的线性组合,如果弱分类器是线性函数,无论怎样组合,强分类器都是线性的,
因此应该选择非线性的分类器做弱分类器。
参考:
https://www.itcodemonkey.com/article/8588.html
https://blog.csdn.net/playezio/article/details/80471000#commentBox