多维点集问题的分治技术

---

1. 引言

多维点集问题在计算机科学领域有着十分重要的地位，其旨在解决高维空间内最大点的搜索、ECDF函数的计算以及最近点的搜索等等，这些问题在实际应用中有着非常重要的作用，比如在数据库中，每条数据表示一个高维向量，那么若干条数据便构成了一个高维向量集，当我们要搜索一些符合条件的记录时，就可以使用解决多维点集问题的算法来解决它。本文参考[1]¹详细的给出了一种解决多维点集问题的算法，并通过几个多维点集问题举例阐述了这一经典算法，本人水平有限，难免出现纰漏，欢迎留言指正。

2. 分治技术

分治技术是算法领域内极其经典的一类方法，其核心是将一个问题拆分为若干个子问题解决，若其子问题还是很复杂，则递归地将其继续拆分成子问题直到问题的规模足够小，可以很快地解决。因此，此类算法的难点也就在与如何将一个问题拆分以及如何合并子问题的计算结果。举一个很简单的一维空间的排序问题，要对整个集合进行排序，我们可以将其分为两半（问题拆分），然后再对每一半中的子集进行排序，最后由于两个子集都是有序的，所以只需同时遍历两个子集，按序合并子集即可得到原问题的解（合并结果）。显然，子集的排序也可以按照上述方法计算。
多维点集的问题也可以仿照上述方法计算，其核心的概念是将k维空间内N个点的问题递归地拆解为k维空间内N/2个点的问题，然后递归地在k-1维空间内解决k维空间内子问题结果的合并问题。接下来的几部分，我们将围绕这一概念处理几个经典的多维点集问题。

3. 支配问题

3.1 经验累积分布函数

对于k维空间内任意两点$P(i_1,i_2,...,i_k)$与 $Q(j_1,j_2,...,j_k)$，如果$i_d>j_d,d=1,..,k$，那么称P支配Q。经验累积分布函数就是求在k维空间的点集中每个点所支配点的数量rank与全部点数量N的比值$(rank/N)$。显然当k等于1时，该问题就退化成了求在一维数据集中比该数小的数有多少个的问题。因此，对于一维空间内，若要求经验累积分布函数，那我们可以先用快速排序将其按大小顺序排好，这样，每个数对应的经验累积分布函数值就是其索引号除以数据集的大小（不考虑重复数的情况），也就是说我们可以在$O(Nlo{g}_{2}N)$时间内将其计算完成。
在二维空间中，情况又稍微复杂些，下图给出了一个二维空间内的点分布情况以及其rank值：

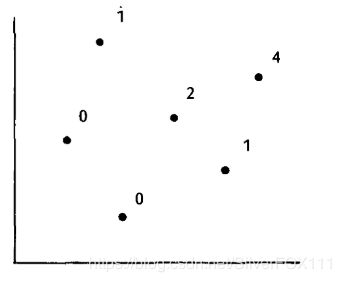
为了可以快速的计算rank值，我们在这引入第二节的核心概念。以上图为例，首先，我们先将其等分为A、B两个部分，然后分别计算A与B中点的rank值，如下图所示：

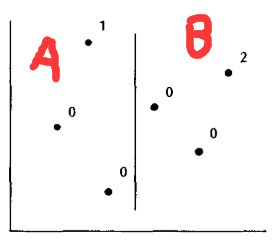
此时，由于A中点的x值都小与B中点的x值，所以A中的点不可能支配B中的点，故A部分计算所得的rank值即为最终rank值。现在我们需要进行的操作就变为了修改B中点的rank值（因为B中的点除了可能支配B中的其他点外还有可能支配A中的点，所以B中点的rank值不是最终rank值）。修改其rank值的算法很简单，先将所有A中的点以及B中的点合并在一起，同时记录每个点原先是哪个集合的，再以点y值的大小排好顺序，接下来我们开始顺序扫描排好序的所有点，同时定义一个变量account，若扫描到A中的点，account加1，否则将该点的rank加account。当将全部的点扫描完成后，rank值也就修改完成，同时问题也已经解决。

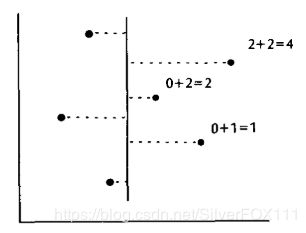
在上述算法描述中，对于分割操作，我们需要找到这些点的x值中的中位数，利用这个中位数将点集进行分割，这样可以很大程度上减少递归次数，寻找中位数的算法可以使用快速中位数算法，其可以在$O(N)$时内找到中位数。因此，总的算法时间复杂度公式如下：
$$\begin{gathered} T(N)=O(N)+2T(N/2)+O(Nlo{g}_{2}N) \\ \approx 2T(N/2)+O(Nlo{g}_{2}N) \end{gathered}$$
其中，O(N)表示中位数的搜索时间以及扫描时间，$O(Nlo{g}_{2}N)$表示对y进行排序的时间。推导可得（推导过程参考链接）:
$$T(N)=O(Nlo{g}_2^{2}N)$$
此外，如果我们预先可以对点集按y值排序，而且在后续的算法中一直维护其顺序，那么我们就可以省去$O(Nlo{g}_{2}N)$项，再次推导公式即可得到更理想的时间复杂度：
$$T(N)=O(Nlo{g}_{2}N)$$
现在，我们再次升级难度，由二维空间转移到三维空间。类似于处理二维空间的算法一样，首先，我们先将所有的点以y-z平面（x = median）等分为两部分A,B，然后分别计算各自集合中点的rank值，由于A中点的x值都小与B中点的x值，所以A中的点不可能支配B中的点，也就是说A中点的rank值就是最后的rank值，接下来只需要计算B中点的rank值即可。修改B中点的rank值可以先将A与B的所有点投影到y-z面上，即忽略x坐标，然后调用二维空间中的算法计算B中点在二维空间中的rank值，由于该rank值中也包含了B中点在二维空间中支配B中的其他点的数量，所以我们还需要计算B中点在二维空间中支配B中的其他点的数量，最后B中点的rank值就等于自己加上B中点在二维空间中的rank值，再减去B中点在二维空间中支配B中的其他点的数量。因此可以得到三维空间中算法的时间复杂度：
$$T(N)=2T(N/2)+O(Nlo{g}_{2}N)$$
推导得：
$$T(N)=O(Nlo{g}_2^{2}N)$$
当然了，这种思路可以一般化到k维空间，其算法步骤总结如下：

1. 以x = median将点集等分割为子集A与B；
2. 递归调用算法计算子集A与B中点的rank值；
3. 将A与B中的点映射到k-1维空间中（即忽略第一维坐标），调用k-1维算法，计算B中每个点在A中支配点的数量，并加到自己对应得rank上。

特别说明，第二步的递归出口是点集的大小小与等于1，而第三步的递归出口是维数为2。因此，类似三维空间中的算法分析，我们可以得到k维空间算法的时间复杂度：
$$T(N,k)=O(N)+2T(N/2,k)+T(N,k-1)$$
其中，O(N)表示的是寻找中位数以及修改rank值等线性时间开销操作。其推导结果可以通过归纳法得到：
$$\begin{gathered} T(N,2)=O(Nlo{g}_{2}N) \\ T(N,3)=O(Nlo{g}_2^{2}N) \end{gathered}$$
假设：
$$T(N,k)=O(Nlo{g}_2^{k-1}N)$$
因此，
$$\begin{gathered} T(N,k+1)=O(N)+2T(N/2,k+1)+T(N,k) \\ T(N,k+1)=O(N)+2T(N/2,k+1)+O(Nlo{g}_2^{k-1}N) \end{gathered}$$
令$N=2^m$，则：
$$\begin{gathered} T(2^m,k+1)=2T(2^{m-1},k+1)+2^m{m}^{k-1} \\ T(2^m,k+1)=2(2T(2^{m-2},k+1)+2^{m-1}(m-1{)}^{k-1})+2^m{m}^{k-1} \\ =4T(2^{m-2},k+1)+2^m(m-1{)}^{k-1}+2^m{m}^{k-1} \\ ... \\ T(2^m,k+1)=2^{m}T(1,k+1)+2^m{0}^{k-1}+..+2^m(m-1{)}^{k-1}+2^m{m}^{k-1} \end{gathered}$$
由之前算法得知$T(1,k+1)$显然是常数操作，故可以省去，而且由Faulhaber’s formula可知，$a_1^k+a_2^k+..+a_n^k$的结果中其最大幂次是k+1，故：
$$T(N,k+1)\approx Nlo{g}_2^{k}N$$
因此假设成立。此外，为了能够更加准确的描述上述方法，本文提供了相关代码，有兴趣的读者可以参考附录A。

3.2 经验累积分布函数的搜索问题（The ECDF searching problem）

经验累积分布函数的搜索类似与上一小节的问题，其目的是能够快速的回答一个新的点在加入一个点集后，其rank值的大小。显然，对于一维空间我们可以先将点集排序，然后在进行二分查找该点的值，结果即为所求。如果我们令P表示查询结构的构建时间，Q为查询时间，S为存储需求，那么一维空间对应的这些值可以用如下式子所代替：
$$\begin{gathered} P(N)=O(Nlo{g}_{2}N) \\ Q(N)=O(lo{g}_{2}N) \\ S(N)=O(N) \end{gathered}$$
现在，我们开始讨论二维空间中问题的解决方法。在二维空间中问题通俗来讲，就是在平面中找有多少个点在新点的左下方。因此，在建立查询结构时，我们引入第二节的核心概念，假设点集的大小为N，先以点集x坐标的中位数将其切分为两半A（x值都小于中位数）与B，分别建立它们各自的查询结构，然后对A点集的点按y坐标排序（预排序会提高构建速度）。我们将这样构建好的树称为ECDF树，下面给出了二维空间点集的ECDF树的一个例子以及节点结构：

node	说明
number	用于划分点集的中位数
pointer	指向左子树，表示x值小于number的点集
pointer	指向右子树，表示x值大于或等于number的点集
list	存放按y值排好序的A点集的索引

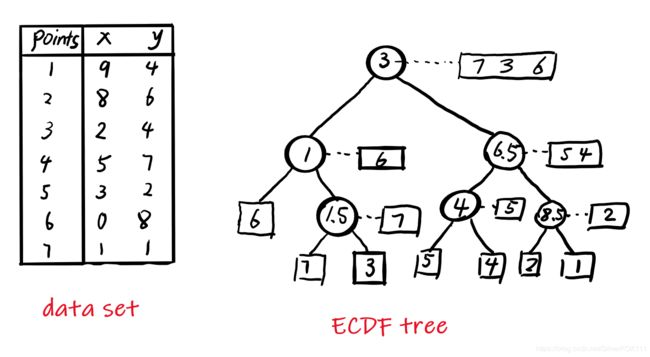
如上图所示，圆圈中的树就是切割线的x值，即中位数，虚线指向节点左边点集（点集A）排好序后的索引列表。如此，我们可以利用ECDF树进行新点的rank值查询了。假如新点为(5,6)，首先我们先将其x坐标与3进行比较，显然5>3，所以(5,6)的rank值应该是(5,6)在点集B中支配的点数加上(5,6)的y值大于点集A中点的y值的数量（(5,6)的x值一定大于点集A中点的x值）。由于节点中存放着list，我们可以通过二分查找的方法很快知道(5,6)的y值大于点集A中点的y值的数量为2。接下来，与6.5做比较，由于5<6.5，因此我们在6.5的左子树找rank值（右子树的x值都大于(5,6),没有必要在右子树中搜索）。接着，与4作比较，5>4，所以与之前相同，先计算(5,6)的y值大于点集A中点的y值的数量为1，再计算(5,6)在点集B中支配的点数，由于其右子树为叶子节点，而且(5,6)不支配(5,7)，所以返回rank值（1+0）。回溯最终得到最后的rank值为3。
接下来，我们对上述算法的三个指标P、S、Q进行一下分析。首先是ECDF树的构建时间，由于我们递归地每次构建其左半边子树与右半边子树，而且需要找中位数以及分割点集（使用预排序去除构建时的排序时间），所以构建时间如下：
$$P(N)=2P(N/2)+O(N)=O(Nlo{g}_{2}N)$$
对于存储空间，有上图可知，其大小为：
$$S(N)=2S(N/2)+N/2=O(Nlo{g}_{2}N)$$
而搜索时间包括递归搜索子树以及二分查找y-rank值，所以其复杂度为:
$$Q(N)=Q(N/2)+O(lo{g}_{2}N)=O(lo{g}_2^{2}N)$$
我们将上述算法一般化到k维平面。在k维空间中，ECDF树由两棵子树（代表k维空间中的N/2个点）以及一个(k-1)维子树（代表左子树点集在k-1维上的投影）。当我们要计算一个新点的值时，也可以仿照上述算法先进行第一维比较确定接下来要搜索的子树，若在左边，计算所得的rank值即为最终结果，若在右边，就需要将右子树计算所得的结果加上在k-1维该点在左子树计算得到的结果。下边给出其三项指标：
$$\begin{gathered} P(N,k)=2P(N/2,k)+P(N/2,k-1)+O(N)=O(Nlo{g}_2^{k-1}N) \\ S(N,k)=2S(N/2,k)+S(N/2,k-1)+O(1)=O(Nlo{g}_2^{k-1}N) \\ Q(N,k)=Q(N/2)+Q(N/2,k-1)+O(1)=O(lo{g}_2^{k}N) \end{gathered}$$

3.3 最大点问题

在一个点集中，对于点P，若不存在任意可以支配点P的点Q，则称点P为点集的一个最大点（下图中，圆圈圈住的点就是点集的最大点）。

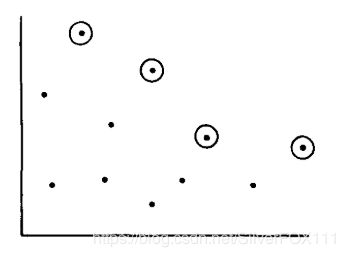
在这一小节中，我们将围绕最大点讨论与它相关的两个问题：

1. 在一个点集中找到全部的最大点
2. 给定任意点，判断其是否为点集的最大点,若不是，给出支配它的点

显然，对于上面的两个问题我们可以借助前两小节的方法快速的给出答案。比如对于第一个问题，我们将点集中的所有数据乘以-1，也就是以原点为中心将点集从第一象限对称到第三象限（以二维空间为例，其他维数类似），然后计算点集的ECDF函数，毋庸置疑，所有函数值为0的点即为点集的最大点。因此，其算法时间复杂度为$O(Nlo{g}_2^{k-1}N)$。对于第二个问题而言，也可以3.2节算法，同时仿照上述方法，若求得的rank值为0，其必然是点集的最大点，而搜索时间即为$O(lo{g}_2^{k}N)$。
但是，这些方法不是本节的重点，这一小节会继续引入分治的核心概念，而且将消除上述时间复杂度中的一个$lo{g}_{2}N$因子。在一维空间中，问题一可以转化为求最大值的问题，也就是说我们可以通过N-1次比较解决这一问题。而对于二维空间，问题又稍微复杂些，不过我们可以先将点集按x坐标从小到大排序，然后从右往左扫描每个点的y值，同时记录目前为止扫描到的最大y值。若扫描的时候，出现比现有的最大y值还大的点，将其记录为最大点，同时更新最大y值。最后，扫描结束，我们的结果也就计算得到了。显然，其时间复杂度就是zh排序与扫描时间的和，即$O(Nlo{g}_{2}N)+O(N)$。这一算法思路很好，唯一的缺点就是不容易一般化到高维空间中，解决办法还是借助于前两节的思路。在二维点集中，我们用点集x坐标的中位数划分点击为A（x值都小于中位数）与B，然后递归地计算各自子集中的最大点。由于B中的点不可能被A中的点所支配，故其结果即为最终答案。而对于A计算所得的结果，其仍有可能被B中的点支配，于是我们需要去除A中被B中点支配的一些最大点，之后得到的结果即为所求。合并经过剔除后的A的结果与B的结果，我们就能得到原问题的解。下面我们给出k维空间中算法的求解过程：

1. 对点集按照第一维进行预排序，同时在之后的处理过程中维护这一顺序；
2. 令k等于点集的维数；
3. 如果点集大小为1直接返回该点集，又或者k等于2时，按照上面描述的方法计算点集中的最大点并返回，否则，将点集用其第k维数据的中位数m分为A（第k维数据小与m）与B两个子集；
4. 递归地计算A与B两个子集的最大点集P与Q；
5. 利用合并算法Merge($P\cup Q$, k - 1)删除P中被任意Q中的点所支配的点，返回结果。

在上述算法的第五步之前需要对P与Q中的点做一个标记black ( P )，white( Q )，然后调用合并算法Merge(Set, d)，Merge函数流程如下：

1. 如果点集大小为1直接返回该点集，又或者d等于2时，仿照上面第三步处理d的方法删除点集中的被白点所支配的黑点，否则，将点集用其第k维数据的中位数m分为A（第k维数据小与m）与B两个子集；
2. 递归地调用合并算法Merge(A, d)与Merge(B, d)处理A与B两个子集，得到点集P与Q；
3. 提取P中的黑点与B中的白点，并将其合并为点集U，调用合并算法Merge(U, d - 1);
4. 将P中的白点、Q中的所有点以及第三步计算得到的点集取交集返回。

上述算法我们提供了相关源码，有兴趣的读者参考附录B。最后我们对这个算法做一个简单的时间复杂度分析。可以看出，我们算法的核心在于merge函数，其时间复杂度公式可以用下式表达：
$$\begin{gathered} T(N,k)=2T(N/2,k)+T(N,k-1)+O(N) \\ T(N,2)=O(N) \end{gathered}$$
推导得到$T(N,k)=O(Nlo{g}_2^{k-2}N)$。所以我们可以得到最后的算法时间复杂度公式：
$$\begin{gathered} T(N,k)=2T(N/2,k)+O(Nlo{g}_2^{k-3}N)+O(N) \\ T(N,2)=O(N) \end{gathered}$$
这样，最后的算法时间复杂度为$O(Nlo{g}_2^{k-2}N)$。
现在，我们也简单描述第二个问题的分治算法。由前一个问题的思路，我们可以很容易的将3.2节的搜索结构延伸到问题二中。对于二维空间，其搜索结构只是将3.2中ECDF节点中的list换做右子树代表的点集的最大y值，其可以在$O(Nlo{g}_{2}N)$时间内建立，而且存储空间是线性的。此外，与3.2节的搜索算法稍微有些区别，要确定一个点是否为点集的最大点，我们先将该点的x值与节点中的值作比较，若大与该值就在右子树中找能够支配它的点，否则在左子树中找能支配它的点，如果在A子树中未找到就将该点的y值与节点中存的B子树中的最大y值做对比，若小于它，说明支配它的点存在，否则不存在。显然，其搜索时间复杂度为$O(lo{g}_{2}N)$。
一般化到k维空间，N个点构成的点集的搜索结构由两个k维空间N/2个点构成的子结构以及一个k-1维空间N/2个点构成的子结构组成。当给 定一个点，我们将其于节点中的值比较，小与在左子树继续搜索，大于在右子树搜索。若右子树未发现可以支配该点的点，则表示该点是最大点（A子树的点不可能支配该点）。若左子树未发现可以支配该点的点，则降维，在k-1维空间中确定该点是否可以被B中的点支配（用后一个子结构）。其三项指标时间复杂度如下：
$$\begin{gathered} P(N,k)=2P(N/2,k)+P(N/2,k-1)+O(N)=O(Nlo{g}_2^{k-2}N) \\ S(N,k)=2S(N/2,k)+S(N/2,k-1)+O(1)=O(Nlo{g}_2^{k-2}N) \\ Q(N,k)=Q(N/2)+Q(N/2,k-1)+O(1)=O(lo{g}_2^{k-1}N) \end{gathered}$$

3.4 范围搜索问题（Range Searching）

这一小节我们讨论支配点问题的最后一个子问题，范围搜索问题。范围搜索问题在几何意义上将，其本质就是找一个空间中由一个超矩形所包围区域内的点集。若将其在平面空间表示就是找下图中矩形包围的点集。

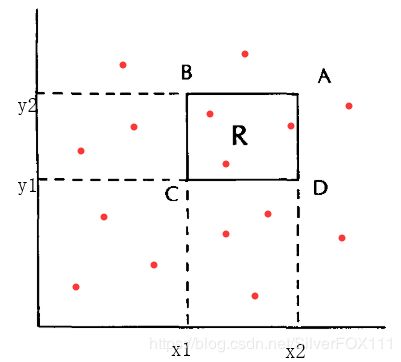
这一问题在地理学方面有着很重要的作用，比如搜索给定两个经度与两个纬度区域内的城市。通常情况下，我们对范围内的数据的多少感兴趣，这些数据可以计算一个区域的密度，因此，很容易地可以想到利用3.1节的算法和容斥定理计算这一数据。还是以上图为例，假设$r(p)$表示一个点的rank值，如果给定X范围(x1,x2)与Y范围(y1,y2)，那我们就可以通过计算$r(A)-[r(B)+r(D)-r(C)]$得到X与Y表示区域内的点数（ A(x2,y2),B(x1,y2),C(x1,y1),D(x2,y1) ）。这种方法在高维空间也是可以使用的。
当然，除此之外还可以模仿3.2节的方法使用range tree（类似ECDF树）进行搜索。range tree的节点由六个元素组成，如下表所示：

node	说明
MID	用于划分点集的中位数(第一维)
LO	本节点代表的范围下限(第一维)
HI	本节点代表的范围上限(第一维)
pointer	指向左子树，其上界是父节点的中位数
pointer	指向右子树，其下界是父节点的中位数
list（2维空间）	存放按最后一维值排好序的点集的索引
pointer（k维空间）	存放(k-1)维range tree

我们按照类似ECDF树的构建过程同样能够递归地完成range树的构建。范围搜索结构与ECDF搜索问题类似，同样由两个k维空间中N/2个点构成的子树与一个k-1维空间中N个点构成的子树组成，其构建时间复杂度同样也为$O(Nlo{g}_2^{k-1}N)$，存储空间为$O(Nlo{g}_2^{k-1}N)$。如果给定一个范围$(X_1,X_2,..,X_k)$ 其中$X_i$表示第i维的一个上界和一个下界，我们首先比较首节点的LO和HI与$X_1$，若$X_1$可以包含(LO,HI)，那么我们在其k-1维子树中寻找范围$(X_2,..,X_k)$（因为第一维全部在范围内）；如果(LO,MID)可以包含X1,则在其左子树继续进行搜索；如果(MID,HI)可以包含X1,则在其右子树继续进行搜索；否则的话就得在两个子树中分别进行搜索，最后合并结果即可。因此，其搜索时间复杂度为搜索时间$O(lo{g}_2^{k}N)$加上合并结果的时间O(F)，F是范围内点的数量。下面给出了一个二维平面的例子，假设给定范围（X1,X2）与（Y1，Y2），现在遍历的节点情况如下：

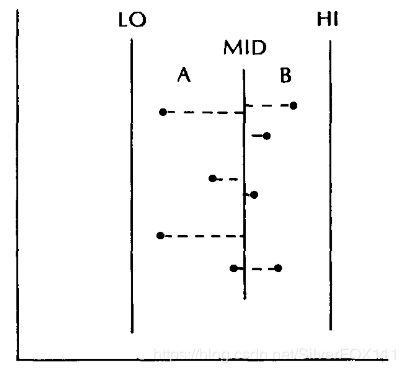
若$(LO,HI)\subseteq (X1,X2)$，我们只需要在节点维护的list中找到Y1与Y2的位置（二叉查询），其对应索引范围内的点就是所求结果。若$(X1,X2)\subseteq (LO,MID)$，或者$(X1,X2)\subseteq (MID,HI)$，那我们就应该递归地到代表A或B集节点中查找。否则的话就该在两个区间分别进行查找，最后合并结果。

---

Appendix A

/*
 * Calculating Empirical Cumulative Distribution Functions for N points in 2-dimensional space
 * by the divide-and-conquer algorithm.
 *
 */
class ECDF2{

public:
    ECDF2(vector< vector<int> >& points, int ifd = 0, bool flag = true);
    // dnum indicates indexes of those points in the vector points which will join in the calculation.
    ECDF2(vector< vector<int> >& points, vector<int>& dnum, int ifd = 0);
    void printRank();
    vector<int>* getrank(){ return &rank2; }
    int operator[](int i) const{return rank2[i];}


private:
    int N;
    int ifd; // the index of first dimension
    int iy;
    vector<int> rank2; // Rank2[i] represents the number of point it dominates.

    void divide(vector< vector<int> >& points, vector<int>& dnum);

};
// end ECDF2 class

/*
 * Calculating Empirical Cumulative Distribution Functions for N points in k-dimensional space
 * by the divide-and-conquer algorithm.
 *
 */
class ECDFk{

public:
    ECDFk(vector< vector<int> >& points, vector<int>& dnum, int dim, int ifd = 0, int flag = true);
    void printRank();
    vector<int>* getrank(){ return &rankk; }
    int operator[](int i) const{return rankk[i];}

private:
    int N;
    int ifd; // the index of first dimension
    int dimension;
    vector<int> rankk; // Rank k[i] represents the number of point it dominates.

    void divide(vector< vector<int> >& points, vector<int>& dnum);

};
// end ECDFk class
/****************************************************************************************
 *
 * some function about the ECDF2 class
 *
 ***************************************************************************************/

ECDF2::ECDF2(vector< vector<int> >& points, int ifd, bool flag):
    N{points.size()},ifd{ifd},iy{ifd + 1}
{
    rank2 = vector<int>(N);

    vector<int> dnum(N);
    vector<int> imap;
    for(int i = 0; i < N; i++) {dnum[i] = i;}
    if(flag){
        imap = dnum;
        Qsort(points, 0, points.size() - 1, iy, imap);
    }
    divide(points, dnum);
    if(flag){
        for(int i = 0; i < N - 1; ++i) { // restore original order of rank2
            if(i != imap[i]){
                int j = i;
                while(i != imap[j] && ++j);
                swap(rank2[i], rank2[j]);
                swap(imap[i], imap[j]);
            }
        }
    }
}

ECDF2::ECDF2(vector< vector<int> >& points, vector<int>& dnum, int ifd):
    N{points.size()},ifd{ifd},iy{ifd + 1}
{
    rank2 = vector<int>(N);
    // defaulting that points is sorted.
    divide(points, dnum);
}

inline bool analyzePoints2(vector< vector<int> >& points, vector<int>& dnum, int ifd){
    int i = 1;
    while(i < dnum.size()){
        if(points[dnum[0]][ifd] != points[dnum[i++]][ifd]) return true;
    }
    return false; // has no relation of domination.
}

void ECDF2::divide(vector< vector<int> >& points, vector<int>& dnum){

    // only a or zero point
    if ( dnum.size() <= 1 ){
        return;
    }
    if(!analyzePoints2(points, dnum, ifd)){
        return; // only count amount of points which is strongly dominated.
    }
    // two or more points, starting the divide-and-conquer algorithm

    //partition

    vector<int> A;
    vector<int> B;
    // find median number
    int median = Qmedian(points, dnum, ifd);
    int xmax = vmax(points, dnum, ifd);
    // record the index of every point and place it in A or B
    // set label for every point
    vector<bool> label(dnum.size());
    for(int i = 0; i < dnum.size(); ++i){
        if(points[dnum[i]][ifd] < median || (points[dnum[i]][ifd] == median && median != xmax)){
            A.push_back(dnum[i]);
            label[i] = true;
        }
        else{
            B.push_back(dnum[i]);
            label[i] = false;
        }
    }

    divide(points, A); // calculate the first half
    divide(points, B); // calculate the last half

    // merge and conquer
    int account = label[0] ? 1 : 0;
    int last_account = 0;
    int p = 1;
    for(int i = 1; i < dnum.size(); ++i){
        if(points[dnum[i]][iy] != points[dnum[i - 1]][iy]){
            last_account = account;
        }
        if(label[p++]){ // point in A
            account++;
        }
        else{ // point in B
            if(points[dnum[i]][iy] == points[dnum[i - 1]][iy])
                rank2[dnum[i]] = rank2[dnum[i]] + last_account;
            else{
                rank2[dnum[i]] = rank2[dnum[i]] + account;
            }
        }
    }

}

void ECDF2::printRank(){

    cout << "\nEmpirical Cumulative Distribution Functions for N points in 2-dimensional space\n";
    cout << "-------------------------------------------------------------------------------";
    for(int i = 0; i < rank2.size(); ++i){
        if(i % 10 == 0)
            cout << endl;
        cout << rank2[i] << "\t";
    }
    cout << "\n-------------------------------------------------------------------------------\n";

}

/*********************************end ECDF2***********************************************/

/****************************************************************************************
 *
 * some function about the ECDFk class
 *
 ***************************************************************************************/

ECDFk::ECDFk(vector< vector<int> >& points, vector<int>& dnum, int dim, int ifd, int flag):
    N{points.size()},dimension{dim},ifd{ifd}
{
    rankk = vector<int>(N);

    vector<int> imap;
    if(flag){
        imap = dnum;
        Qsort(points, 0, points.size() - 1, ifd + dimension - 1, imap);
    }
    divide(points, dnum);
    if(flag){
        for(int i = 0; i < N - 1; ++i) { // restore original order of rank2
            if(i != imap[i]){
                int j = i;
                while(i != imap[j] && ++j);
                swap(rankk[i], rankk[j]);
                swap(imap[i], imap[j]);
            }
        }
    }
}

void ECDFk::divide(vector< vector<int> >& points, vector<int>& dnum){

    // only a or zero point
    if ( dnum.size() <= 1 ){
        return;
    }
    if(!analyzePoints2(points, dnum, ifd)){
        return; // only count amount of points which is strongly dominated.
    }
    // two or more points, starting the divide-and-conquer algorithm

    //partition

    vector<int> A;
    vector<int> B;
    // find median number
    int median = Qmedian(points, dnum, ifd);
    int xmax = vmax(points, dnum, ifd);
    // record the index of every point and place it in A or B
    vector<bool> label(dnum.size());
    for(int i = 0; i < dnum.size(); ++i){
        if(points[dnum[i]][ifd] < median || (points[dnum[i]][ifd] == median && median != xmax)){
            A.push_back(dnum[i]);
            label[i] = true;
        }
        else{
            B.push_back(dnum[i]);
            label[i] = false;
        }
    }

    divide(points, A); // calculate the first half
    divide(points, B); // calculate the last half

    // merge and conquer
    // project points on a plane
    int i = 0, j = 0;
    if(dimension != 3){
        ECDFk ecdfkAB{points, dnum, dimension - 1, ifd + 1, false};
        ECDFk ecdfkB{points, B, dimension - 1, ifd + 1, false};
        while(i < dnum.size()){
            if(!label[i]){
                rankk[dnum[i]] = rankk[dnum[i]] + ecdfkAB[dnum[i]] - ecdfkB[B[j++]];
            }
            i++;
        }
    }
    else{
        ECDF2 ecdf2AB{points, dnum, ifd + 1};
        ECDF2 ecdf2B{points, B, ifd + 1};
        while(i < dnum.size()){
            if(!label[i]){
                rankk[dnum[i]] = rankk[dnum[i]] + ecdf2AB[dnum[i]] - ecdf2B[B[j++]];
            }
            i++;
        }
    }

}

void ECDFk::printRank(){

    cout << "\nEmpirical Cumulative Distribution Functions for N points in k-dimensional space\n";
    cout << "-------------------------------------------------------------------------------";
    for(int i = 0; i < rankk.size(); ++i){
        if(i % 10 == 0)
            cout << endl;
        cout << rankk[i] << "\t";
    }
    cout << "\n-------------------------------------------------------------------------------\n";

}

/*********************************end ECDFk***********************************************/

Appendix B

/*
 * Calculating all the maximal points for N points in 2-dimensional space
 * by the divide-and-conquer algorithm.
 *
 */
class Maxima2{

public:
    Maxima2(vector< vector<int> >& points);
    void printIndex();
    int operator[](int i) const{return IndexOfMaxima[i];}


private:
    int N;
    vector<int> IndexOfMaxima; // The vector IndexOfMaxima stores indexes of all the maximal points. .

    void maxima(vector< vector<int> >& points);

};
// end Maxima2 class

/*
 * Calculating all the maximal points for N points in 3-dimensional space
 * by the divide-and-conquer algorithm.
 *
 */
class Maxima3{

public:
    Maxima3(vector< vector<int> >& points, vector<int>& dnum, int ix = 0, bool flag = true);
    void printIndex();
    vector<int> getIndex(){ return IndexOfMaxima; }
    int operator[](int i) const{return IndexOfMaxima[i];}

private:
    int N;
    int ix;
    int iy;
    int iz;
    vector<int> IndexOfMaxima; // The vector IndexOfMaxima stores indexes of all the maximal points. .

    vector<int> maxima(vector< vector<int> >& points, vector<int>& dnum);

};
// end Maxima3 class

/*
 * Calculating all the maximal points for N points in k-dimensional space
 * by the divide-and-conquer algorithm.
 *
 */
class Maximak{

public:
    Maximak(vector< vector<int> >& points);
    void printIndex();
    vector<int> getIndex(){ return IndexOfMaxima; }
    int operator[](int i) const{return IndexOfMaxima[i];}

private:
    int N;
    int dimension;
    vector<int> IndexOfMaxima; // The vector IndexOfMaxima stores indexes of all the maximal points. .

    vector<int> Divide(vector< vector<int> >& points, vector<int>& dnum, int d);
    vector<int> Merge(vector< vector<int> >& points, vector<int>& dnum, int d);

};
// end Maximak class

/****************************************************************************************
 *
 * some function about the Maxima2 class
 *
 ***************************************************************************************/

Maxima2::Maxima2(vector< vector<int> >& points):N{points.size()} {

    Qsort(points, 0, points.size() - 1, 0); // sorted by x-axis
    maxima(points);

}

void Maxima2::maxima(vector< vector<int> >& points){

    // only a or zero point
    if ( points.size()  < 1 ){
        return;
    }
    else if( points.size() == 1 ){
        IndexOfMaxima.push_back(0);
        return;
    }

    // two or more points
    int ymax = points[N - 1][1];
    IndexOfMaxima.push_back(N - 1);
    for(int i = N - 2; i >= 0; --i){
        if(points[i][1] >= ymax){
            IndexOfMaxima.push_back(i);
            ymax = points[i][1];
        }
    }

}

void Maxima2::printIndex(){

    cout << "\nIndexes of all the maximal points for N points in 2-dimensional space\n";
    cout << "-------------------------------------------------------------------------------";
    for(int i = 0; i < IndexOfMaxima.size(); ++i){
        if(i % 10 == 0)
            cout << endl;
        cout << IndexOfMaxima[i] << "\t";
    }
    cout << "\n-------------------------------------------------------------------------------\n";

}

/*********************************end Maxima2***********************************************/

/****************************************************************************************
 *
 * some function about the Maxima3 class
 *
 ***************************************************************************************/

Maxima3::Maxima3(vector< vector<int> >& points, vector<int>& dnum, int ix, bool flag):
    N{points.size()},ix{ix},iy{ix + 1},iz{ix + 2}
{

    if(flag)
        Qsort(points, 0, points.size() - 1, 0); // sorted by x-axis

    IndexOfMaxima = maxima(points, dnum);

}

inline bool analyzePoints(vector< vector<int> >& points, vector<int>& dnum, int dim){
    int i = 1;
    while(i < dnum.size()){
        if(points[dnum[0]][dim] != points[dnum[i++]][dim]) return true;
    }
    return false; // has no relation of domination.
}

vector<int> Maxima3::maxima(vector< vector<int> >& points, vector<int>& dnum){

    // only a or zero point
    if ( dnum.size()  < 1 ){
        return vector<int>();
    }
    else if( dnum.size() == 1 ){
        return vector<int>(1, dnum[0]);
    }

    if(!analyzePoints(points, dnum, iz)){
        vector<int> res = dnum;
        return res;
    }

    // divide
    vector<int> A;
    vector<int> B;
    // find median number
    int median = Qmedian(points, dnum, iz);
    int zmax = vmax(points, dnum, iz);
    // record the index of every point and place it in A or B
    for(int i = 0; i < dnum.size(); ++i){
        if(points[dnum[i]][iz] < median || (points[dnum[i]][iz] == median && median != zmax)){
            A.push_back(dnum[i]);
        }
        else{
            B.push_back(dnum[i]);
        }
    }

    vector<int> Ares = maxima(points, A);
    vector<int> Bres = maxima(points, B);

    // merge
    // set label for every point
    vector<int> res;

    int ymax = vmax(points, Bres, iy);
    for(auto p : Ares){
        if(points[p][1] >= ymax){
            res.push_back(p);
        }
    }
    mergeSortedVecter(res, Bres);

    return res;

}

void Maxima3::printIndex(){

    cout << "\nIndexes of all the maximal points for N points in 3-dimensional space\n";
    cout << "-------------------------------------------------------------------------------";
    for(int i = 0; i < IndexOfMaxima.size(); ++i){
        if(i % 10 == 0)
            cout << endl;
        cout << IndexOfMaxima[i] << "\t";
    }
    cout << "\n-------------------------------------------------------------------------------\n";

}

/*********************************end Maxima3***********************************************/

/****************************************************************************************
 *
 * some function about the Maximak class
 *
 ***************************************************************************************/

Maximak::Maximak(vector< vector<int> >& points):
    N{points.size()},dimension{points[0].size()}
{

    vector<int> dnum(N);
    for(int i = 0; i < N; ++i) dnum[i] = i;

    Qsort(points, 0, points.size() - 1, 0); // sorted by x-axis
    IndexOfMaxima = Divide(points, dnum, dimension);

}

vector<int> Maximak::Divide(vector< vector<int> >& points, vector<int>& dnum, int d){

    vector<int> res;

    // only a or zero point
    if ( dnum.size()  < 1 ){
        return vector<int>();
    }
    else if ( dnum.size() == 1 ){
        return vector<int>(1, dnum[0]);
    }

    if (!analyzePoints(points, dnum, d - 1)){
        res = dnum;
        return res;
    }

    if (d == 2){ // conquer
        int ymax = 0;
        for(int i = dnum.size() - 1; i >= 0; --i){
            if(points[dnum[i]][1] >= ymax){
                res.push_back(dnum[i]);
                ymax = points[dnum[i]][1];
            }
        }
        reverse(res.begin(), res.end());
        return res;
    }

    // divide
    vector<int> A;
    vector<int> B;
    // find median number
    int median = Qmedian(points, dnum, d - 1);
    int lmax = vmax(points, dnum, d - 1);
    // record the index of every point and place it in A or B
    for(int i = 0; i < dnum.size(); ++i){
        if(points[dnum[i]][d - 1] < median || (points[dnum[i]][d - 1] == median && median != lmax)){
            A.push_back(dnum[i]);
        }
        else{
            B.push_back(dnum[i]);
        }
    }

    vector<int> Ares = Divide(points, A, d);
    vector<int> Bres = Divide(points, B, d);

    // merge
    // set label
    for(auto p : Ares){
        points[p].push_back(0);
    }
    for(auto p : Bres){
        points[p].push_back(1);
    }
    mergeSortedVecter(Ares, Bres);
    // delete the point in Ares dominated by any point in Bres
    res = Merge(points, Ares, d - 1);
    // delete label
    for(auto p : Ares){
        points[p].pop_back();
    }
    return res;

}

vector<int> Maximak::Merge(vector< vector<int> >& points, vector<int>& dnum, int d){

    vector<int> res;

    // only a or zero point
    if ( dnum.size()  < 1 ){
        return vector<int>();
    }
    else if ( dnum.size() == 1 ){
        return vector<int>(1, dnum[0]);
    }

    if (!analyzePoints(points, dnum, d - 1)){
        res = dnum;
        return res;
    }

    if (d == 2){ // conquer
        int ymax = 0;
        for(int i = dnum.size() - 1; i >= 0; --i){
            if(points[dnum[i]][dimension]){ // label is B
                res.push_back(dnum[i]);
                if(points[dnum[i]][1] >= ymax)
                    ymax = points[dnum[i]][1];
            }else{
                if(points[dnum[i]][1] >= ymax)
                    res.push_back(dnum[i]);
            }
        }
        reverse(res.begin(), res.end());
        return res;
    }

    // divide
    vector<int> A;
    vector<int> B;
    // find median number
    int median = Qmedian(points, dnum, d - 1);
    int lmax = vmax(points, dnum, d - 1);
    // record the index of every point and place it in A or B
    for(int i = 0; i < dnum.size(); ++i){
        if(points[dnum[i]][d - 1] < median || (points[dnum[i]][d - 1] == median && median != lmax)){
            A.push_back(dnum[i]);
        }
        else{
            B.push_back(dnum[i]);
        }
    }

    vector<int> Ares = Merge(points, A, d);
    vector<int> Bres = Merge(points, B, d);

    // delete the point labeled 0 in Ares dominated by any point labeled 1 in Bres
    vector<int> UA;
    vector<int> UB;
    vector<int> Alabeled1; // the point labeled 1 in Ares
    for(auto p : Ares){
        if(!points[p][dimension]) UA.push_back(p);
        else Alabeled1.push_back(p);
    }
    for(auto p : Bres){
        if(points[p][dimension]) UB.push_back(p);
    }
    mergeSortedVecter(UA, UB);
    vector<int> Ures = Merge(points, UA, d - 1);

    // merge consequence
    mergeSortedSet(Bres, Alabeled1);
    mergeSortedSet(Bres, Ures);

    return Bres;

}

void Maximak::printIndex(){

    cout << "\nIndexes of all the maximal points for N points in k-dimensional space\n";
    cout << "-------------------------------------------------------------------------------";
    for(int i = 0; i < IndexOfMaxima.size(); ++i){
        if(i % 10 == 0)
            cout << endl;
        cout << IndexOfMaxima[i] << "\t";
    }
    cout << "\n-------------------------------------------------------------------------------\n";

}

/*********************************end Maximak***********************************************/

---

1. L.J. Bentley, “Multidimensional Divide-and-Conquer,” Comm. ACM, vol. 23, no. 4, pp. 214-229, 1980. ↩︎