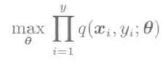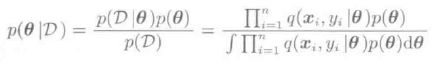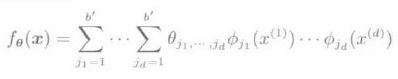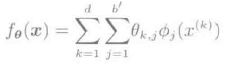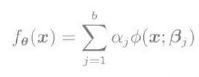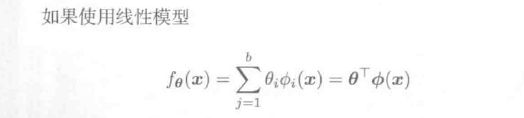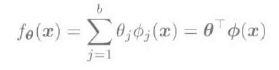机器学习基础概念及知识
AI被炒的越来越热,自己毕设也选择了相关课题,趁着AI浪潮还没过去抓紧学习一下。。哈哈。先为大家推荐《图解机器学习》这本书,这本书不会着重于算法公式的推导,更重要的是介绍一些基础的概念帮助大家理解,感觉挺适合入门的,自己的这篇博客和配图也主要来自于这本书。当然那本西瓜书《机器学习》也挺好滴,毕竟是经典推荐书籍噻,不过自我感觉还是先入个门再去读这本书会好一些。。。自己也只是个机器学习的菜鸟,如果文中有错误欢迎各位大佬们批评指正哈。。。
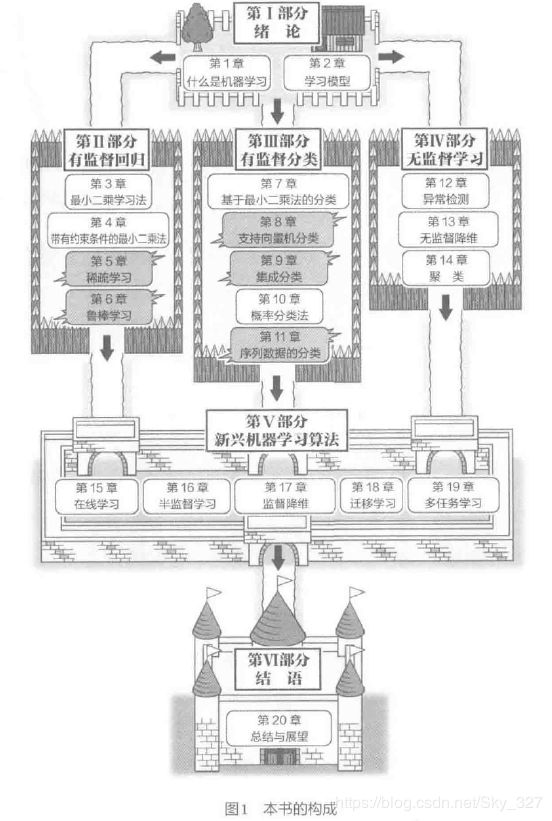
第一部分 绪论
CH01 什么是机器学习
1、学习的种类
有监督学习:文字识别、声音处理、图像处理、垃圾邮件分类与拦截、网页检索等方面应用,典型任务包括:预测数值型数据的回归、预测分类标签的分类、预测顺序的排序;
无监督学习:视频分析、社交网站解析和声音信息解析等方面应用,典型任务包括:聚类、异常检测等。
强化学习:自己对预测结果进行评估以获得最佳结果而不断进行学习进步。
2、机器学习任务的例子
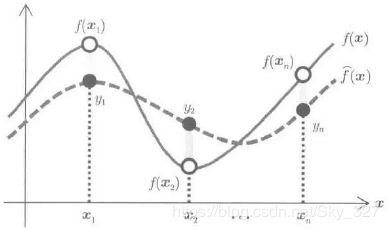
回归,把实函数在样本点附近加以近似的有监督的函数近似问题,但输出中经常会观测到噪声,即存在偏差。
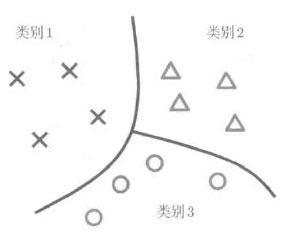
分类,对于指定的模式进行识别的有监督模型识别问题,即将输入样本划分为若干种类别,其只是单纯地对样本的类别进行预测并根据预测是否准确来衡量泛化误差,这点与回归不同。
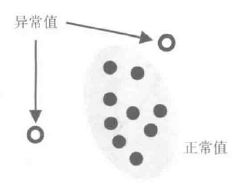
异常检测,寻找输入样本中所包含的异常数据的问题。在已知正常数据与异常数据的情况下实际就是一个有监督学习的过程,但一般情况下时是未知的,在这种情况下可采用密度估计的方法进行检测。
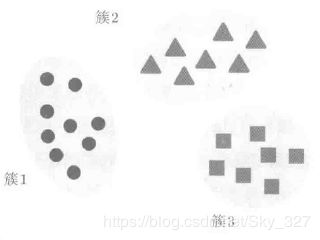
聚类,属于无监督学习,判断输入样本属于哪个簇,簇内相似性高,簇间相似性低。
降维,从高维度数据中提取关键信息,将其转换为易于计算的低维度问题进行求解,简单的说就是特征维度可能会很多,全部输入对运算性能和运算时间都有比较高的要求,所以就需要进行降维来提高效率。
3、机器学习的方法(以对模式x的类别y进行预测的分类为例)
(1)生成的分类和识别的分类:
已知模式x的时候,求得使分类类别y的条件概率达到最大值的类别y翰特的话就能进行模式识别了。应用训练集直接对后验概率p(y|x)进行学习的过程称为判别式(识别)分类。
条件概率p(y|x)通常也成为后验概率,而后验概率p(y|x)和联合概率p(x,y)是成正比例的,所以可通过使联合概率达到最大值的方法使后验概率达到最大值。
在模式识别里,联合概率p(x,y)也称为数据生成概率,通过预测生成概率进行分类,称之为生成的分类。
在进行模式识别时,如果只需计算出后验概率p(y|x),识别的分类就优于生成的分类;如果在实际问题中(如声音识别),可提前获得很多有关生成概率p(x,y)的先验知识,生成的分类就优于识别的分类。
(2)统计概率和朴素贝叶斯:
在统计概率的学习方法中,将模式θ作为决定论的变量,如何由训练集D得到高精度的模式θ是主要的研究方向。
在朴素贝叶斯方法中,将模式θ作为概率变量,对其先验概率p(θ)考虑,计算与训练集D对应的后验概率p(θ|D)。
CH02 学习模型
1、线性模型
由于一般的线性模型对于实际情况的拟合没太大实用价值,于是便将其进行扩展,使得线性模型也可以表示非线性的输入与输出。如果将基函数变为多项式的形式,那么就可以表示复杂的非线性模型,如下所示。但应注意,线性模型的基函数与训练样本是毫不相关的。
而对于多维的输入向量x,可通过使用一维的基函数构造多维基函数的乘法模型和加法模型。
(1)乘法模型:把一维的基函数作为因子,通过使其相乘而获得多维基函数
但应特别注意的是,所有参数的个数是 (bl)d ,即总的输入维数是指数级增长的,而随着维数的增加计算量呈指数级增长,称之为维数灾难.
(2)加法模型:把一维的基函数作为因子,通过使其相加而获得多维基函数的方法
加法模型中的参数只会随着输入维数d线性增长,计算力不会超出计算机正常范围,但表现力要弱很多。
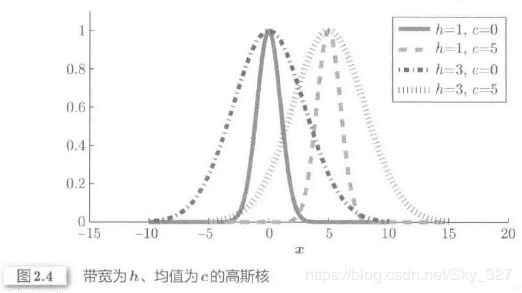
2、核模型
在进行基函数的设计时使用到了输入样本。
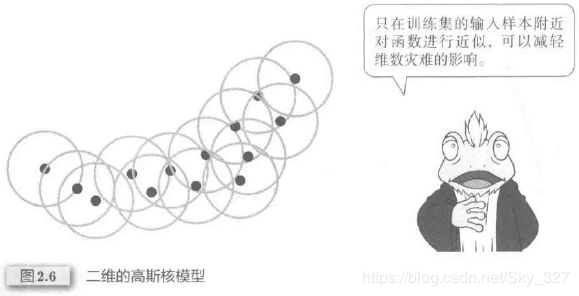
在高斯核模型汇总,一般只能在训练集的输入样本附近对函数进行近似,而正因为这个原因,从某种程度上来说,高斯核模型减轻了乘法模型中维数灾难的影响。
实际上在核模型中,参数的个数不依赖于输入变量x的维数d,只由训练样本数n决定。另一个特征是,当输入样本不是向量的时候也能很容易地实现扩展,因输入样本x只存在于核函数K(x,x’),只需对两个输入样本x和x’对应的核函数加以定义而不用关心输入样本x具体是什么。
3、层级模型
简单来讲,只要是与参数相关的,不是线性的模型都是非线性的,而层级模型又是其中很重要的一个。
应该注意的是,使用S型函数的层级模型常被称为人工神经网络;而这里的高斯函数与核模型中的高斯函数不同,核模型中的带宽和均值都是固定的而层级模型中都是可以进行学习的。
第二部分 有监督回归
CH03 最小二乘法
1、基本概念
如果公式比较难以理解的话,看图可能会更直接一些。我认为机器学习的学习过程不应仅仅局限于晦涩难懂的数学公式,而是应该掌握其整体架构,而后再深入学习。
对于顺序为i的训练样本的平方差通过权重进行加权,然后再采用最小二乘法学习,这称为加权最小二乘学习法。
2、最小二乘法的性质
首先是设计矩阵的奇异值分解。
渐近无偏性:
3、大规模数据的学习算法
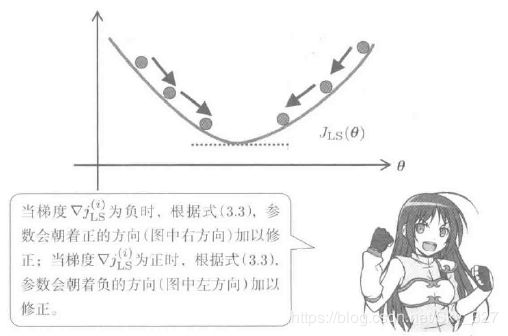
当数据规模较大,导致计算内存不足时,可采用随机梯度算法进行优化。随机梯度算法试纸,沿着训练平方误差J的梯度下降,对参数依次进行学习的算法。
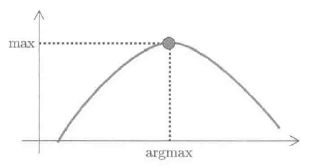
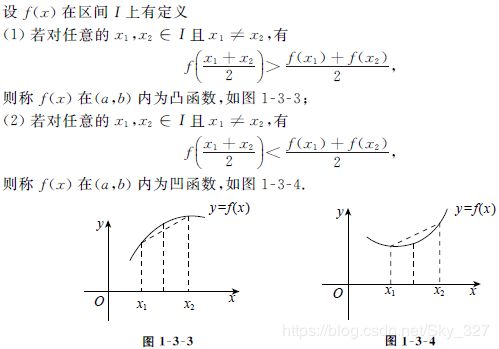
凹函数与凸函数:
因为凸函数是一只有一个峰值的函数,所以通过梯度法就可以得到训练平方误差J在值域范围内的最优解,即全局最优解。
但是,梯度法的收敛速度,强烈依赖于梯度下降的步幅和收敛结果的判断方法,这点在实际过程中是不太好操作的。
CH04 带有约束条件的最小二乘法
因上一章介绍的最小二乘法对于包含噪声的学习过程常有过拟合的弱点,因此引入了带有约束条件的最小二乘学习法,
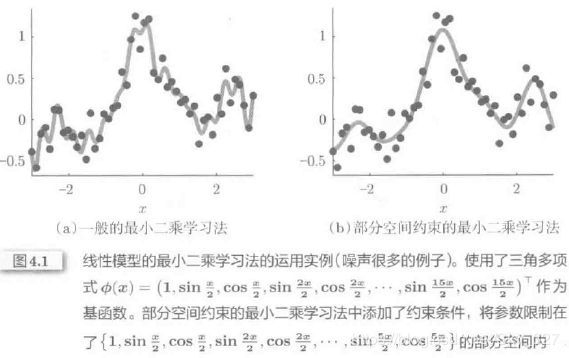
1、部分空间约束的最小二乘学习法
通过把参数空间限制在一定范围内来防止过拟合的现象。
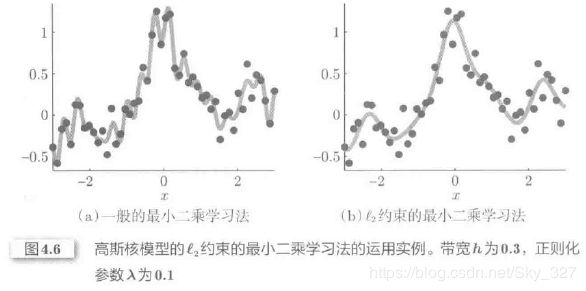
2、l2约束的最小二乘学习法(也被称为岭回归)
因正交投影矩阵P的设置有很大的自由度,在实际应用中操作很困难,所以经常会采用一种操作较为容易的l2约束的最小二乘学习法。
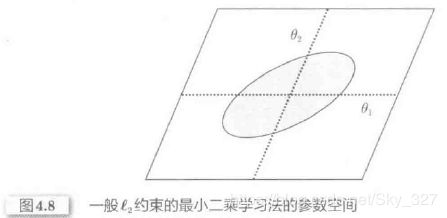
L2约束的最小二乘学习法是以参数空间的原点为圆心,在一定半径范围的圆,一般为超球进行求解的。利用拉格朗日对偶问题,通过求解下式的最优解问题就可以得到最优化问题的解。
在一些情况下,我们通过b×b的正则化矩阵G,就可以得到更为普遍的表示方法。
3、模型选择:不同的输入样本来决定算法中的参数值
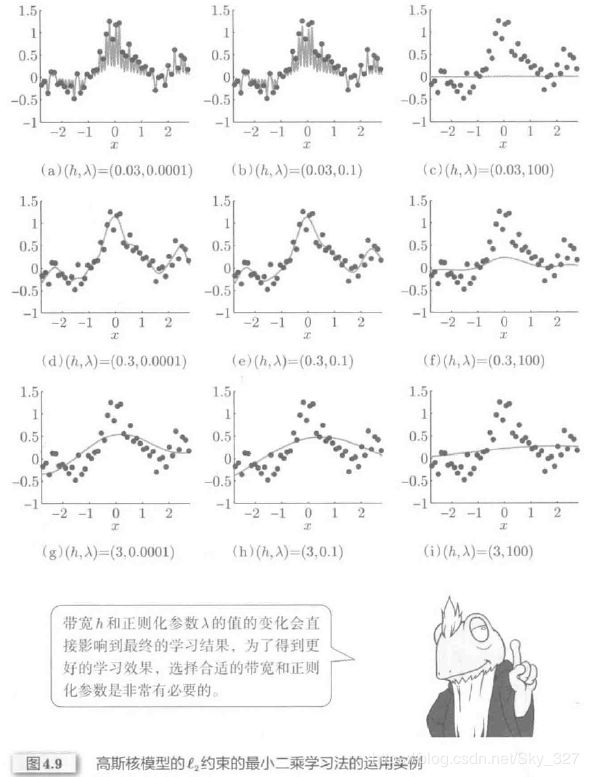
为了使带有约束条件的最小二乘学习法得到较为理想的效果,选择合适的P值和λ值是十分重要的。同时,使用线性模型时基函数的种类和数量,使用核模型时核函数的种类等选择也需要进行优化。
下图是一般的模型选择流程,其中,泛化误差是特别需要关注的,它是指对未知测试输入样本所做的预测误差。
为了得到较为理想的泛化误差,实际过程中常采用交叉验证法(10折交叉验证和留1交叉验证最为常用),对泛化误差进行较为准确的评估。
留1交叉验证是值,对 n-1 个训练样本进行学习,将余下的1个样本作为测试样本,循环进行n次学习。如果n值很大可能会使得计算时间过长,故采用如下计算方法求得交叉验证法的泛化误差的评估值的解析解G: