机器学习笔记（3） -- Boston House Price数据集预测

Python机器学习项目模版

1. 准备
a) 导入类库
b) 导入数据集
2. 概述数据
a) 描述性统计
b) 数据可视化
3. 预处理数据
a) 数据清洗
b) 特征选择
c) 数据转换
4. 评估算法
a) 分离数据集
b) 评估选项和评估矩阵
c) 算法审查
d) 算法比较
5. 提高模型准确度
a) 算法调参
b) 集成算法
6. 序列化模型
a) 预测评估数据集
b) 利用整个数据集生产模型
c) 序列化模型

1. 问题定义

在这个项目中将会分析研究波士顿房价（Boston House Price）数据集。在这个数据集的每一行数据都是对波士顿周边或者城镇的房价的描述。数据是1978年统计手机的。数据中包含如下14和特征，506条数据（UCI机器学习仓库中的定义）：

• CRIM：城镇人均犯罪率
• ZN：住宅地所占比例
• INDUS：城镇中非住宅用地所占比例
• CHAS：查尔斯河虚拟变量，用于回归分析
• NOX：环保指数
• RM：每栋住宅的房间数
• AGE：1940年以前建成的自住单位的比例
• DIS：距离5个波士顿的就业中心的加权距离
• RAD：距离高速公路的便利指数
• TAX：每一万美元的不动产税率
• PTRATIO：城镇中教师学生比例
• B：城镇中黑人比例
• LSTAT：地区中有多少房东属于低收入人群
• MEDV：自住房屋价中位数

通过这些特质属性的描述，我们可以发现输入的特质属性的度量单位是不统一的。
数据集地址：https://archive.ics.uci.edu/ml/machine-learning-databases/housing/

2. 导入数据

# 导入类库
import pandas as pd
import numpy as np
import matplotlib as mpl
from numpy import arange
import matplotlib.pyplot as plt
from pandas import set_option
from pandas.plotting import scatter_matrix
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Lasso
from sklearn.linear_model import ElasticNet
from sklearn.tree import DecisionTreeRegressor
from sklearn.neighbors import KNeighborsRegressor
from sklearn.svm import SVR
from sklearn.pipeline import Pipeline
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.ensemble import AdaBoostRegressor
from sklearn.metrics import mean_squared_error
import warnings
warnings.filterwarnings('ignore')

接下来我们将数据集导入到Python中。

# 导入数据
filename = 'housing.csv'
names = ['CRIM','ZN','INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX','PRTATIO','B','LSTAT','MEDV']
dataset = pd.read_csv(filename,names= names, delim_whitespace=True)

这里对每个特质属性设定了一个名字，方便后面程序中使用它们，因在CSV文件是通过空格键来做分隔符，因此在这里读入CSV文件时，指定分隔符为空格键（delim_whitespace = True）。

3. 分析数据

现在需要对导入的数据进行分析，以便能够构建合适的模型。

3.1 描述性统计

首先看一下数据的维度，例如数据集中有多少条记录，有多少个数据特征

# 数据维度
print(dataset.shape)

执行之后我们可以看到总共有506条记录和14个特征属性，这与我们在UCI上得到的信息一致。

接下来看一下各个特征属性的字段类型

# 特征属性的字段类型
print(dataset.dtypes)

可以了解到所有的特征属性都是数字，大部分都是浮点数，也有部分特征属性是整数类型的。

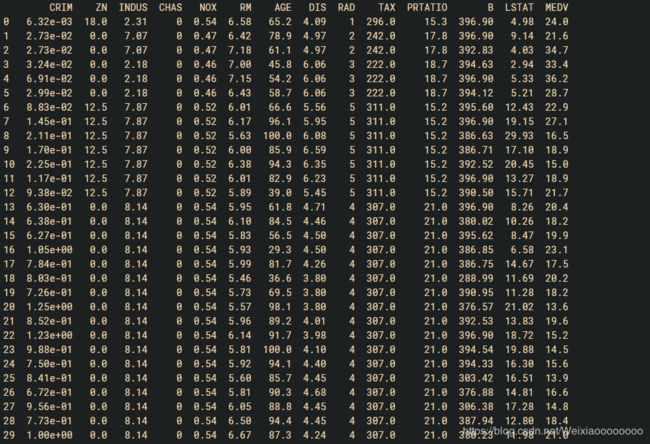
接下来对数据进行一次简单的查看，在这我们看一下最开始的30条数据。

# 查看最开始的30条记录
print(dataset.head(30))

接下来看一下数据的描述性统计信息。

# 描述统计信息
pd.set_option('precision',1)
print(dataset.describe())

在描述性统计信息中包含数据的最大值、最小值、中位数、四分位数等，分析这些数据能够加深对数据分布、数据结构等的理解。

接下来看一下数据特征之间的两两关联关系，这里查看数据的皮尔逊相关系数。

# 关联关系
pd.set_option('precision',2)
print(dataset.corr(method='pearson'))

执行结果如图：

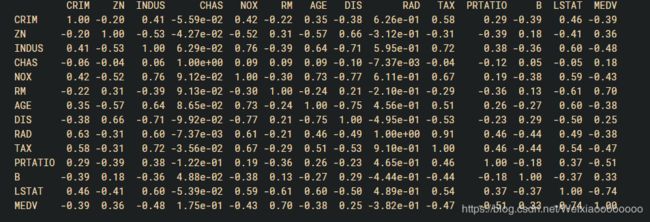
通过上面的结果可以看到，有些特征属性之间具有强关联关系（>0.7或<-0.7），如：

• NOX与INDUS之间的皮尔逊相关系数是0.76
• DIS与INDUS之间的皮尔逊相关系数是-0.71
• TAX与INDUS之间的皮尔逊相关系数是0.72
• AGE与NOX之间的皮尔逊相关系数是0.73
• DIS与NOX之间的皮尔逊相关系数是-0.77

4. 数据可视化

4.1 单一特征图表

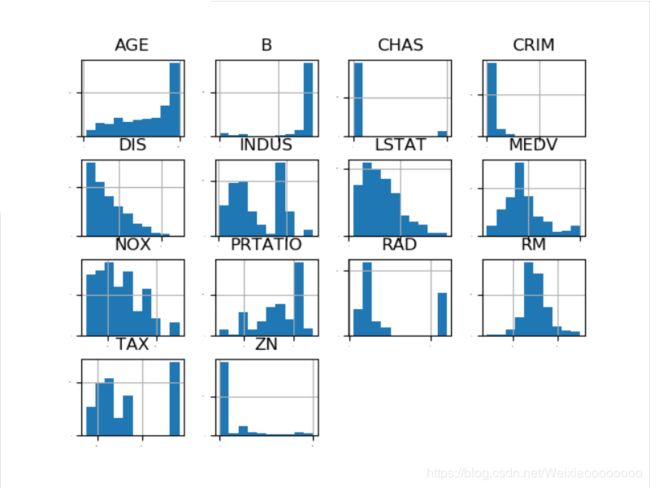
首先查看一下每一个数据特征的单独分布图，多查看几种不同的图表有助于发现更好的主意。首先看一个各个数据特征的直方图，来感受一下数据的分布情况。

# 直方图
dataset.hist(sharex=False,sharey=False,xlabelsize=1,ylabelsize=1)
plt.show()

执行结果如下，从图中可以看到有些数据呈指数分布，如CRIM，ZN，AGE，和B，有些数据特征呈双峰分布，如RAD和TAX。

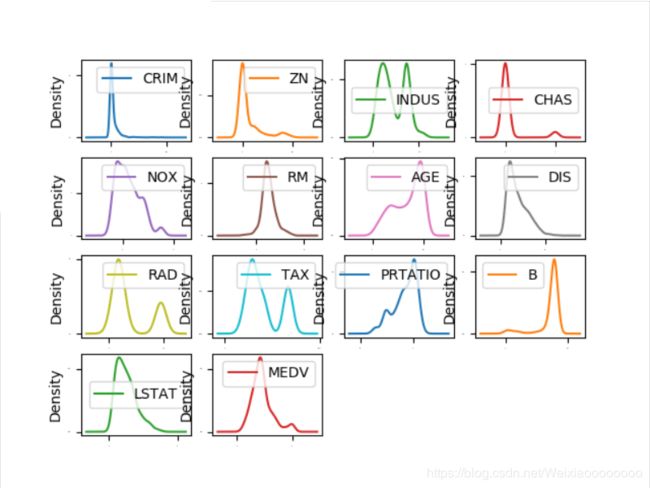
通过密度图可以展示这些数据的特征属性，密度图比 直方图更加平滑地展示了这些数据特征。

# 密度图
dataset.plot(kind = 'density', subplots = True, layout = (4,4),sharex = False, fontsize =1)
plt.show()

在密度图中，指定layout=(4,4)，这说明要画一个四行四列的图形。

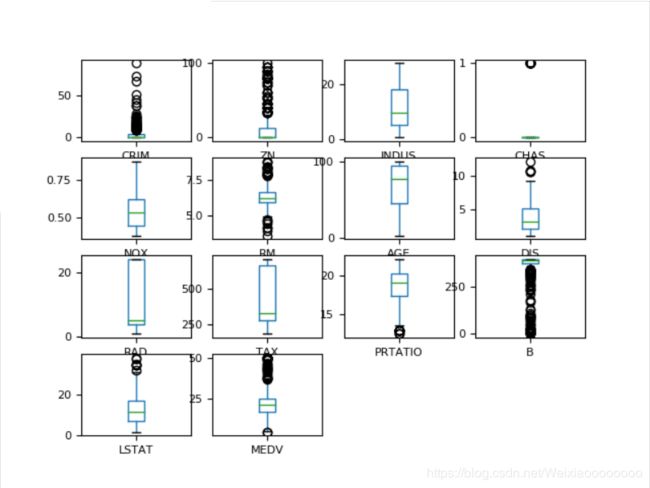
通过箱线图可以查看一个数据特征的状况，也可以很方便地看出数据分布的偏态程度。

# 箱线图
dataset.plot(kind ='box', subplots = True, layout = (4,4),sharex = False, sharey = False,fontsize = 8)
plt.show()

执行结果如图：

4.2 多重数据图表

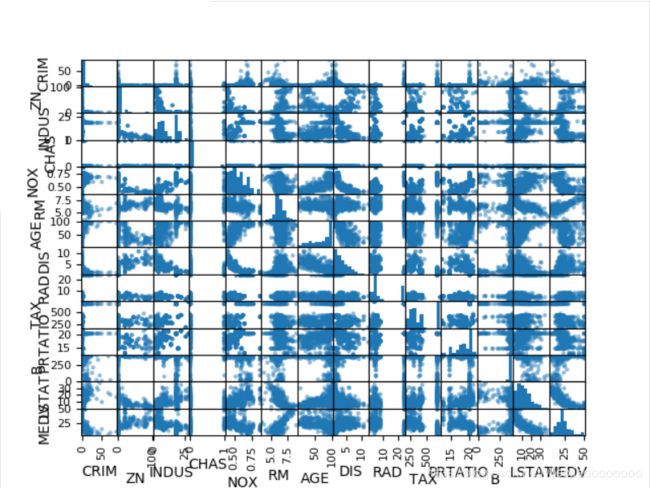
接下来利用多重数据图表来查看不同数据特征之间的相互影响关系。首先看一下散点矩阵图。

# 散点矩阵图
scatter_matrix(dataset)
plt.show()

通过散点矩阵图可以看到，虽然有些数据特征之间的关联关系很强，但是这些数据分布结构也很好。即使不是线性分布结构，也是可以很方便进行预测的分布结构。

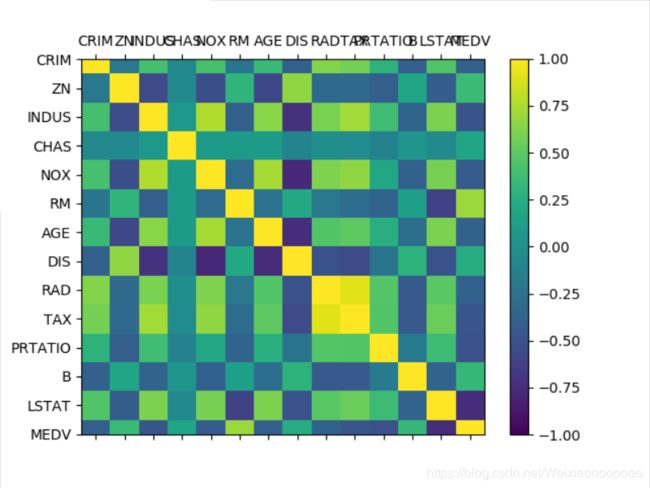
再看一下数据相互影响的相关矩阵图。

# 相关矩阵图
fig = plt.figure()
ax = fig.add_subplot(111)
cax = ax.matshow(dataset.corr(),vmin = -1, vmax = 1, interpolation = 'none')
fig.colorbar(cax)
ticks = np.arange(0,14,1)
ax.set_xticks(ticks)
ax.set_yticks(ticks)
ax.set_xticklabels(names)
ax.set_yticklabels(names)
plt.show()

根据图例可以看到，数据特征属性之间的两两相关性，有些属性之间是强相关，建议在后续的处理中移除这些特征属性，以提高算法的准确度。

4.3 思路总结

通过数据的相关性，数据的分布等发现，数据集中的数据结构比较复杂，需要考虑对数据进行转换，来提高模型的准确度。可以尝试从一下几个方面来对数据进行处理：

• 特征选择来减少大部分相关性高的特征。
• 标准化数据来降低不同数据尺度带来的影响。
• 正态化数据来降低不同的数据分布结构来提高算法的准确度。

可以进一步的花费时间来看一下数据的可能性分级（离散化），可能性分级可以帮助提高决策树算法的准确度。

5. 分离评估数据集

分离出一个评估数据集是一个很好的主意，我们可以确保分离出的数据集与训练模型的数据集完全隔离，这有助于我们分析和模型化。我们将会在整个项目的最后一步使用这个评估数据集来确认模型的准确度。在这里我们会分离20%数据作为评估数据集，80%数据作为训练数据集。

# 分离数据集
array = dataset.values
X = array[:, 0:13]
Y = array[:, 13]
validation_size = 0.2
seed = 7
X_train, X_validation, Y_train, Y_validation = train_test_split(X, Y, test_size=validation_size, random_state= seed)

6. 评估算法

6.1 评估算法 —— 原始数据

分析完数据，不能立马选择出哪个算法对这个问题最有效。我们直观上任务，由于部分数据的线性分布，线性回归算法和弹性网络回归算法可能对问题的解决比较有效。另外，由于数据的离散化，通过决策树算法或者支持向量机算法也许可以生产高准确度的模型。到这里，依然不清楚哪个算法会生产准确度最高的模型，因此需要设计一个评估框架来帮助选择合适的算法。在这里采用10折交叉验证来分离数据，通过均方误差（MSE）来比较算法的准确度。均方误差（MSE）越趋近于0，表示算法准确度越高。

# 评估算法 —— 评估标准
num_folds = 10
seed = 7
scoring = 'neg_mean_squared_error'

对原始数据不做任何处理，对算法进行一个评估，形成一个算法的评估基准。这个基准值是对后续算法改善优劣比较的基准值。在这里选择三个线性算法，三个非线性算法，共六个算法来进行比较：

• 线性算法：线性回归（LR），套索回归（LASSO）和弹性网络回归（EN）。

• 非线性算法：分类与回归树（CART），支持向量机（SVM）和K近邻算法（KNN）。

# 评估算法 —— baseline
models = {}
models['LR'] = LinearRegression()
models['LASSO'] = Lasso()
models['EN'] = ElasticNet()
models['KNN'] = KNeighborsRegressor()
models['CART'] =DecisionTreeRegressor()
models['SVM'] = SVR()

接下来对所有的算法使用默认参数，并比较算法的准确度。在这里比较的是均方误差（MSE）的均值和标准方差。

# 评估算法
results = []
for key in models:
    kfold = KFold(n_splits=num_folds,random_state=seed)
    cv_result = cross_val_score(models[key],X_train,Y_train,cv = kfold,scoring=scoring)
    results.append(cv_result)
    print('%s: %f(%f)'%(key,cv_result.mean(),cv_result.std()))

执行结果看起来线性回归（LR）具有最低的MSE，接下来是分类与回归树（CART）算法。

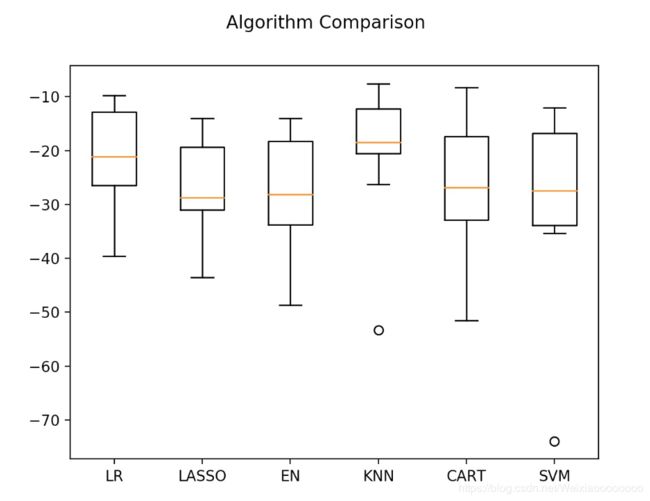
接下来看一下所有的k折交叉分离验证的结果。

# 评估算法 —— 箱线图
fig = plt.figure()
fig.suptitle('Algorithm Comparison')
ax = fig.add_subplot(111)
plt.boxplot(results)
ax.set_xticklabels(models.keys())
plt.show()

可以看到线性算法的分布比较类似，并且K近邻算法的结果分布非常紧凑。

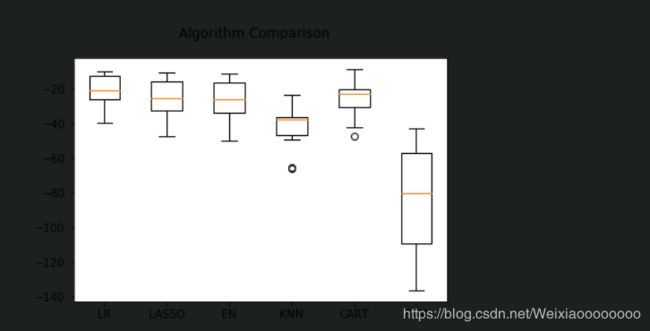
不同的数据度量单位，也许是K近邻和支持向量机算法表现不佳的主要原因。接下来对数据进行正态化处理，再次比较算法的结果。

6.1 评估算法 —— 原始数据

在这里猜测也许因为原始数据中不同特征属性的尺度不一样，导致有的算法的结果不是很好。接下来通过对数据进行正态化，再次评估这些算法。在这里对训练数据集进行数据转换处理，将所有的数据特征值转化成为0为中位值，标准差为1的数据。对数据正态化时，为了防止数据泄露，采用Pipeline来正态化数据和对模型进行评估。为了与前面的结果进行比较，在这里采用相同的评估框架来评估算法模型。

# 评估算法 —— 正太化数据
pipelines = {}
pipelines['ScalerLR'] = Pipeline([('Scaler',StandardScaler()),('LR',LinearRegression())])
pipelines['ScalerLASSO'] = Pipeline([('Scaler',StandardScaler()),('LASSO',Lasso())])
pipelines['SclaerEn'] = Pipeline([('Scaler',StandardScaler()),('EN',ElasticNet())])
pipelines['ScalerKNN'] = Pipeline([('Scaler',StandardScaler()),('KNN',KNeighborsRegressor())])
pipelines['ScalerCART'] = Pipeline([('Scaler',StandardScaler()),('CART',DecisionTreeRegressor())])
pipelines['ScalerSVM'] = Pipeline([('Scaler',StandardScaler()),('SVM',SVR())])
results = []
for key in models:
    kfold = KFold(n_splits=num_folds,random_state=seed)
    cv_result = cross_val_score(models[key],X_train,Y_train,cv = kfold,scoring=scoring)
    results.append(cv_result)
    print('%s: %f(%f)'%(key,cv_result.mean(),cv_result.std()))

执行后发现K近邻算法具有最优的MSE。

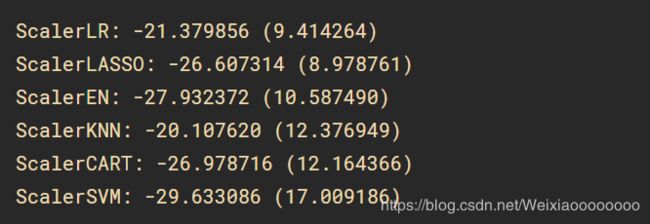
接下来看一下所有的k折交叉分离验证的结果。

# 评估算法 —— 箱线图
fig = plt.figure()
fig.suptitle('Algorithm Comparison')
ax = fig.add_subplot(111)
plt.boxplot(results)
ax.set_xticklabels(models.keys())
plt.show()

7. 调参改善算法

目前K近邻算法（KNN）对做过数据转换的数据集有很好的结果，但是是否可以对结果做一些优化呢？K近邻算法（KNN）的默认参数近邻个数（n_neighbors）是5，在这里通过网格搜索算法来优化参数。

# 调参改善算法 —— KNN
scaler = StandardScaler().fit(X_train)
rescaledX = scaler.transform(X_train)
param_grid = {'n_neighbors':[1,3,5,7,9,11,13,15,17,19,21]}
model = KNeighborsRegressor()
kfold = KFold(n_splits=num_folds,random_state=seed)
grid = GridSearchCV(estimator=model, param_grid = param_grid, scoring=scoring,cv=kfold)
grid_result = grid.fit(X = rescaledX, y=Y_train)
print('最优：%s 使用%s'%(grid_result.best_score_,grid_result.best_params_))
cv_results = zip(grid_result.cv_results_['mean_test_score'],
                grid_result.cv_results_['std_test_score'],
                grid_result.cv_results_['params'])
for mean, std, param in cv_results :
    print('%f(%f) with %r'%(mean,std,param))

最优结果 —— K 近邻算法的默认参数近邻个数是3。

8.集成算法

调参之外提高算法准确度的方法是使用集成算法。在这里会对表现比较好的线性回归（LR）、K近邻（KNN）和分类与回归树算法，采用集成算法，来分析一下算法能否提高。
装袋算法：随机森林（RF）和极端随机树（ET）
提升算法：AdaBoost（AB）和随机梯度上升（GBM）
在这里依然采用和前面同样的评估框架，和正态化之后的数据来，分析相关的算法。

# 集成算法
ensembles = {}
ensembles['ScaledAB'] = Pipeline([('Scaler',StandardScaler()),('AB',AdaBoostRegressor())])
ensembles['ScaledAB-KNN'] = Pipeline([('Scaler',StandardScaler()),('ABKNN',AdaBoostRegressor(base_estimator=KNeighborsRegressor(n_neighbors=3)))])
ensembles['ScaledAB-LR'] = Pipeline([('Scaler',StandardScaler()),('ABLR',AdaBoostRegressor(LinearRegression()))])
ensembles['ScaledRFR'] = Pipeline([('Scaler',StandardScaler()),('RFR',RandomForestRegressor())])
ensembles['ScaledETR'] = Pipeline([('Scaler',StandardScaler()),('ETR',ExtraTreesRegressor())])
ensembles['ScaledGBR'] = Pipeline([('Scaler',StandardScaler()),('GBR',GradientBoostingRegressor())])

results = []
for key in ensembles:
    kfold = KFold(n_splits=num_folds,random_state=seed)
    cv_result = cross_val_score(ensembles[key],X_train,Y_train,cv=kfold,scoring=scoring)
    results.append(cv_result)
    print('%s: %f(%f)'%(key,cv_result.mean(),cv_result.std()))

持续结果比上边的线性算法和非线性算法都具有高准确度。执行结果如下：

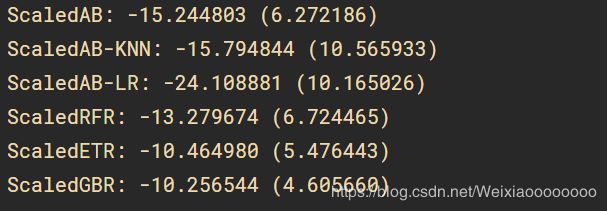
接下来通过箱线图看一下集成算法的状况。

# 集成算法 —— 箱线图
fig = plt.figure()
fig.suptitle('Algorithm Comparison')
ax = fig.add_subplot(111)
plt.boxplot(results)
ax.set_xticklabels(ensembles.keys())
plt.show()

随机梯度上升（GBM）和极端随机树具有较高的中位值和分布状况。

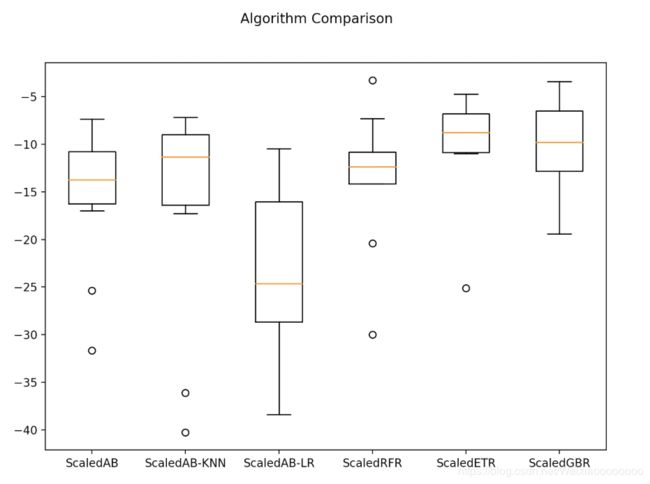
9. 集成算法调参

集成算法都有一个参数n_estimators，这是一个很好的可以用来调整的参数，对于集成参数来说，n_estimators会带来越准确的结果，当然这样有一定的限度。在这里对随机梯度上升（GBM）和极端随机树（ET）进行调参，再次比较这两个算法模型的准确度，来确定最终的算法模型。

# 集成算法GBM —— 调参
caler = StandardScaler().fit(X_train)
rescaledX = scaler.transform(X_train)
param_grid = {'n_estimators':[10,50,100,200,300,400,500,600,700,800,900]}
model = GradientBoostingRegressor()
kfold = GridSearchCV(estimator=model,param_grid=param_grid,scoring=scoring,cv= kfold)
grid_result = grid.fit(X = rescaledX, y = Y_train)
print('最优：%s 使用%s'%(grid_result.best_score_,grid_result.best_params_))

# 集成算法ET —— 调参
scaler = StandardScaler().fit(X_train)
rescaledX = scaler.transform(X_train)
param_grid = {'n_estimators':[5,10,20,30,40,50,60,70,80,90,100]}
model = ExtraTreesRegressor()
kfold = KFold(n_splits=num_folds,random_state=seed)
grid = GridSearchCV(estimator=model,param_grid = param_grid,scoring=scoring,cv=kfold)
grid_result = grid.fit(X = rescaledX,y =Y_train)
print('最优：%s 使用%s'%(grid_result.best_score_,grid_result.best_params_))

随机梯度上升（GBM）来说最优的n_estimators是600；极端随机树（ET）来说最优的n_estimators是100。执行结果，极端随机树（ET）稍微优于随机梯度上升（GBM），因此在这里采用极端随机树（ET）来训练最终的模型。执行结果如下：

10. 最终模型

从上面的数据来看，选择极端随机树（ET）来生产模型，接下来将对算法进行训练和生产模型，并计算模型的准确度。

# 训练模型
caler = StandardScaler().fit(X_train)
rescaledX = scaler.transform(X_train)
gbr = ExtraTreesRegressor(n_estimators=80)
gbr.fit(X = rescaledX,y = Y_train)

接下来通过评估数据集来评估算法的准确度。

# 评估算法模型
rescaledX_validation = scaler.transform(X_validation)
predictions = gbr.predict(rescaledX_validation)
print(mean_squared_error( Y_validation,predictions))

执行结果如下：

11. 总结

通过这个项目理解机器学习项目的模板，以及整个机器学习模型建立的流程。

参考从书：《机器学习Python实践》 魏贞原