Python【相关矩阵】和【协方差矩阵】
文章目录
- 相关系数矩阵
- 协方差矩阵
- 补充
- 协方差
- 相关系数
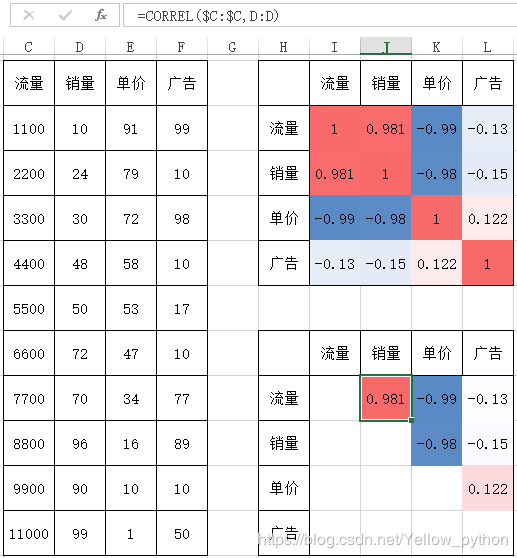
- EXCEL也能做
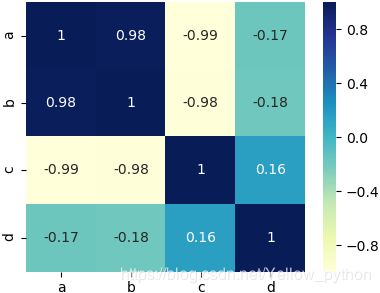
相关系数矩阵
- pandas.DataFrame(数据).corr()
import pandas as pd
df = pd.DataFrame({
'a': [11, 22, 33, 44, 55, 66, 77, 88, 99],
'b': [10, 24, 30, 48, 50, 72, 70, 96, 90],
'c': [91, 79, 72, 58, 53, 47, 34, 16, 10],
'd': [99, 10, 98, 10, 17, 10, 77, 89, 10]})
df_corr = df.corr()
# 可视化
import matplotlib.pyplot as mp, seaborn
seaborn.heatmap(df_corr, center=0, annot=True, cmap='YlGnBu')
mp.show()
协方差矩阵
- numpy.cov(数据)
import numpy as np
matric = [
[11, 22, 33, 44, 55, 66, 77, 88, 99],
[10, 24, 30, 48, 50, 72, 70, 96, 90],
[91, 79, 72, 58, 53, 47, 34, 16, 10],
[55, 20, 98, 19, 17, 10, 77, 89, 14]]
covariance_matrix = np.cov(matric)
# 可视化
print(covariance_matrix)
import matplotlib.pyplot as mp, seaborn
seaborn.heatmap(covariance_matrix, center=0, annot=True, xticklabels=list('abcd'), yticklabels=list('ABCD'))
mp.show()
补充
协方差
C o v ( X , Y ) = E [ ( X − E [ X ] ) ( Y − E [ Y ] ) ] = E [ X Y ] − 2 E [ Y ] [ X ] + E [ X ] [ Y ] = E [ X Y ] − E [ X ] [ Y ] Cov(X,Y) = E[(X-E[X])(Y-E[Y])] \newline = E[XY] - 2E[Y][X] + E[X][Y] \\ = E[XY] - E[X][Y] Cov(X,Y)=E[(X−E[X])(Y−E[Y])]=E[XY]−2E[Y][X]+E[X][Y]=E[XY]−E[X][Y]
相关系数
r ( X , Y ) = C o v ( X , Y ) V a r [ X ] V a r [ Y ] r(X,Y) = \frac{Cov(X,Y)}{\sqrt{Var[X]Var[Y]}} r(X,Y)=Var[X]Var[Y]Cov(X,Y)
EXCEL也能做
CORREL函数
