Java-并发-队列-PriorityBlockingQueue
Java-并发-队列-PriorityBlockingQueue
0x01 摘要
PriorityBlockingQueue是优先级阻塞队列,本文简要分析下。
0x02 简介
PriorityBlockingQueue特点如下:
- 支持优先级
- 无界阻塞队列
PriorityBlockingQueue 是无界队列,不会“队满”。实际当到达队列最大值后(Integer.MAX_VALUE - 8,减8的原因是:数组作为一个对象,需要一定的内存存储对象头信息,对象头信息最大占用内存不可超过8字节。),就抛OOM异常了,因此这点在使用优先队列的时候需要注意。 - 放入队列的元素必须实现
Comparable接口的public int compareTo(T o)方法 - 默认情况下
comparator为null。此时会根据元素的compareTo方法来来排序,比如String类型就是按其实现的挨个比较内部char数组的Ascii码来排序。采取从小到大顺序升序排列,也可以自定义类实现compareTo()方法来指定元素排序规则,需要注意的是不能保证同优先级元素的顺序。 - 线程安全
通过一个可重入锁ReentrantLock来控制入队和出队操作 - 入队出队不可并发
- 通过二叉堆来实现
默认情况下,父元素的值永远比任何子元素的值还小。也就是说,最小的值是queue[0] - 不可放入null元素
- 动态扩容策略
0x03 源码分析
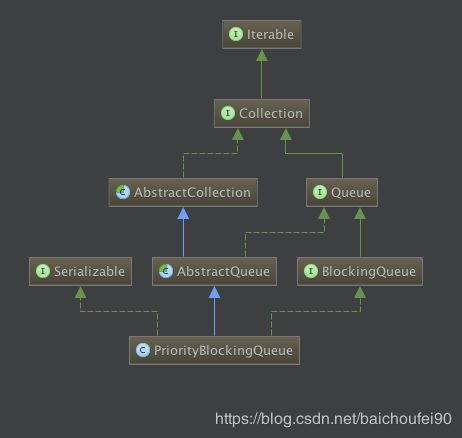
3.1 类定义和继承关系
public class PriorityBlockingQueue<E> extends AbstractQueue<E>
implements BlockingQueue<E>, java.io.Serializable
3.2 重要成员属性
// 序列化值
private static final long serialVersionUID = 5595510919245408276L;
// 默认容量是11
private static final int DEFAULT_INITIAL_CAPACITY = 11;
// 最大容量是Integer.MAX_VALUE - 8,减8的原因是:数组作为一个对象,需要一定的内存存储对象头信息
// 超过这个值直接报OOM异常
private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;
// 使用数组来实现的队列,具体策略是平衡二叉小根堆
// 第n个元素的左孩子是 2n+1,右孩子2n+2
// comparator为空时,queue[n] 小于他的所有子孙后代节点的值。
// 也就是说最小值就是根节点queue[0]
private transient Object[] queue;
// 元素个数
private transient int size;
// 比较器,默认为空
private transient Comparator<? super E> comparator;
// 全局的一个可重入锁
private final ReentrantLock lock;
// lock的Condition
private final Condition notEmpty;
// 一个普通的优先级队列,仅用于序列化,保持和该类的旧版本兼容
// 仅在序列化/反序列化期间为非null。
private PriorityQueue<E> q;
// 用于分配的自旋锁
private transient volatile int allocationSpinLock;
// 存储allocationSpinLock属性的内存偏移量
private static final long allocationSpinLockOffset;
// Unsafe mechanics
private static final sun.misc.Unsafe UNSAFE;
3.3 初始化
3.3.1
static {
try {
UNSAFE = sun.misc.Unsafe.getUnsafe();
// 获取PriorityBlockingQueue的class对象实例
Class<?> k = PriorityBlockingQueue.class;
// 获取allocationSpinLock属性在内存中的偏移量
allocationSpinLockOffset = UNSAFE.objectFieldOffset
(k.getDeclaredField("allocationSpinLock"));
} catch (Exception e) {
throw new Error(e);
}
}
3.3 构造方法
// 默认构造方法, comparator为null
public PriorityBlockingQueue() {
this(DEFAULT_INITIAL_CAPACITY, null);
}
// 指定队列初始容量, comparator为null
public PriorityBlockingQueue(int initialCapacity) {
this(initialCapacity, null);
}
public PriorityBlockingQueue(int initialCapacity,
Comparator<? super E> comparator) {
if (initialCapacity < 1)
throw new IllegalArgumentException();
// 初始化一个全局可重入锁
this.lock = new ReentrantLock();
this.notEmpty = lock.newCondition();
this.comparator = comparator;
// 初始化一个指定容量的Object数组
this.queue = new Object[initialCapacity];
}
// 用指定容器来构建一个 PriorityBlockingQueue
// 如果目标容器是SortedSet或PriorityQueue,那就会按相同排序来排序
// 否则按元素的compareTo方法排序
public PriorityBlockingQueue(Collection<? extends E> c) {
this.lock = new ReentrantLock();
this.notEmpty = lock.newCondition();
boolean heapify = true; // true if not known to be in heap order
boolean screen = true; // true if must screen for nulls
if (c instanceof SortedSet<?>) {
SortedSet<? extends E> ss = (SortedSet<? extends E>) c;
this.comparator = (Comparator<? super E>) ss.comparator();
heapify = false;
}
else if (c instanceof PriorityBlockingQueue<?>) {
PriorityBlockingQueue<? extends E> pq =
(PriorityBlockingQueue<? extends E>) c;
this.comparator = (Comparator<? super E>) pq.comparator();
screen = false;
if (pq.getClass() == PriorityBlockingQueue.class) // exact match
heapify = false;
}
Object[] a = c.toArray();
int n = a.length;
// If c.toArray incorrectly doesn't return Object[], copy it.
if (a.getClass() != Object[].class)
a = Arrays.copyOf(a, n, Object[].class);
if (screen && (n == 1 || this.comparator != null)) {
for (int i = 0; i < n; ++i)
if (a[i] == null)
throw new NullPointerException();
}
this.queue = a;
this.size = n;
if (heapify)
heapify();
}
3.4 放入元素
放入元素主要有offer,add,put三个方法。由于PriorityBlockingQueue是无界队列,所以add 和 put直接调用的 offer 方法。
3.2.1 offer
/**
* 插入元素到队列
* 该元素无界,所以不会返回false
*
* @param e the element to add
* @return {@code true} (as specified by {@link Queue#offer})
* @throws ClassCastException if the specified element cannot be compared
* with elements currently in the priority queue according to the
* priority queue's ordering
* @throws NullPointerException if the specified element is null
*/
public boolean offer(E e) {
if (e == null)
throw new NullPointerException();
final ReentrantLock lock = this.lock;
// 尝试获取锁
lock.lock();
int n, cap;
Object[] array;
// n存当前元素个数,cap存对象数组长度
while ((n = size) >= (cap = (array = queue).length))
// 当元素个数大于等于对象数组长度就进行扩容
tryGrow(array, cap);
try {
Comparator<? super E> cmp = comparator;
if (cmp == null)
// Comparator为空时采用元素实现的compareTo方法排序后,插入元素
siftUpComparable(n, e, array);
else
// 否则采用指定的Comparator的compareTo方法排序后,插入元素
siftUpUsingComparator(n, e, array, cmp);
// 插入成功后元素个数加1
size = n + 1;
// 将wait在notEmpty condition上的线程唤醒(就是那些尝试获取元素但无元素可用的线程)
notEmpty.signal();
} finally {
// 最后释放锁
lock.unlock();
}
return true;
}
3.5 获取元素
3.5.1 dequeue-出队
/**
* 主要的思想就是将根元素即优先级数值最小,优先级最高的那个根元素返回,
* 把尾节点放到原来根节点的位置,然后根据堆规则来调整堆即可
*/
private E dequeue() {
int n = size - 1;
if (n < 0)
// 元素个数已经为0 不能出队
return null;
else {
Object[] array = queue;
// 最小的根元素
E result = (E) array[0];
// 尾元素
E x = (E) array[n];
array[n] = null;
Comparator<? super E> cmp = comparator;
if (cmp == null)
siftDownComparable(0, x, array, n);
else
siftDownUsingComparator(0, x, array, n, cmp);
// 此时元素出队,size--
size = n;
return result;
}
}
3.5.2 poll
/**
* 搜索、返回、删除队列中的头结点
* 当队列为空时,返回null
*
*/
public E poll() {
// 该方法很简单,就是先锁定,然后调用dequeue返回头节点,最后调整堆
final ReentrantLock lock = this.lock;
lock.lock();
try {
return dequeue();
} finally {
lock.unlock();
}
}
再看看带超时时间的poll方法:
/**
* 搜索、返回、删除队列中的头结点
* 如果队列为空,就按指定的timeout进行等待可用的元素
*
* @param timeout how long to wait before giving up, in units of
* {@code unit}
* @param unit a {@code TimeUnit} determining how to interpret the
* {@code timeout} parameter
* @throws InterruptedException if interrupted while waiting
*/
public E poll(long timeout, TimeUnit unit) throws InterruptedException {
// 将等待时间按单位转换为纳秒
long nanos = unit.toNanos(timeout);
final ReentrantLock lock = this.lock;
// 以独占可中断模式获取锁
lock.lockInterruptibly();
E result;
try {
// 持续调用dequeue元素直到拿到元素或者已经达到指定的超时时间
while ( (result = dequeue()) == null && nanos > 0)
nanos = notEmpty.awaitNanos(nanos);
} finally {
// 释放锁
lock.unlock();
}
return result;
}
3.5.3 take
/**
* 搜索、返回、删除队列中的头结点
* 如果无元素可用时就等待
*
* @return 队列中头结点
* @throws InterruptedException if interrupted while waiting
*/
public E take() throws InterruptedException {
final ReentrantLock lock = this.lock;
lock.lockInterruptibly();
E result;
try {
while ( (result = dequeue()) == null)
notEmpty.await();
} finally {
lock.unlock();
}
return result;
}
3.5.4 peek
/**
* 搜索、返回队列中的头结点,但不删除他
* 当队列为空时,返回null
*
*/
public E peek() {
final ReentrantLock lock = this.lock;
lock.lock();
try {
return (size == 0) ? null : (E) queue[0];
} finally {
lock.unlock();
}
}
3.6 扩容
/**
* Tries to grow array to accommodate at least one more element
* (but normally expand by about 50%), giving up (allowing retry)
* on contention (which we expect to be rare). Call only while
* holding lock.
*
* @param array 元素数组
* @param oldCap 数组长度
*/
private void tryGrow(Object[] array, int oldCap) {
// 先释放锁再扩容完成后再获取锁
lock.unlock();
Object[] newArray = null;
// 如果需要自旋,且成功以CAS的方式将allocationSpinLock设为了1
// 这里需要这么操作的原因是有可能多个线程在进行tryGrow
if (allocationSpinLock == 0 &&
UNSAFE.compareAndSwapInt(this, allocationSpinLockOffset,
0, 1)) {
try {
// 扩容算法为:
// 元素个数小于64就仅扩容为: oldCap + oldCap + 2 = 2*oldCap + 2
// 大于等于64时:oldCap + oldCap/2 = 3/2*oldCap
// 也就是说小于64时扩容更迅速
int newCap = oldCap + ((oldCap < 64) ?
(oldCap + 2) : // grow faster if small
(oldCap >> 1));
// 如果扩容结果大于MAX_ARRAY_SIZE
if (newCap - MAX_ARRAY_SIZE > 0) {
// 此时就看看oldCap 只加 1是否超出了限制
int minCap = oldCap + 1;
// 如果超过了限制就抛出OOM异常
// 这里minCap<0的意思是已经从最大的服务号正数int值做加法后变为了负数
if (minCap < 0 || minCap > MAX_ARRAY_SIZE)
throw new OutOfMemoryError();
// 否则就只能设为MAX_ARRAY_SIZE
newCap = MAX_ARRAY_SIZE;
}
if (newCap > oldCap && queue == array)
// 扩容成功而且queue还是指向原数组时,就创建一个新数组
newArray = new Object[newCap];
} finally {
// 自旋锁由1重置为0
allocationSpinLock = 0;
}
}
if (newArray == null) // back off if another thread is allocating
// newArray为Null说明其他线程也在做扩容操作,此时就放弃线程CPU权限,重新竞争CPU
Thread.yield();
// 重新尝试获取锁
lock.lock();
if (newArray != null && queue == array) {
// 此时已经拿到锁,且newArray是本线程扩容的
// 就把 全局queue引用指向新的queue
queue = newArray;
// 然后把内容也复制到新数组中,扩容完毕
System.arraycopy(array, 0, newArray, 0, oldCap);
}
}
3.7 辅助方法
3.7.1 siftUpComparable
此方法是用指定的比较器,从下往上找元素应当放的位置,并调整沿途的元素位置
/**
* 插入元素 x 到位置 k ,使用的是元素自带的比较器
* 与此同时会根据堆的规则调整堆,主要是让孩子大于父节点的值
*
* To simplify and speed up coercions and comparisons. the
* Comparable and Comparator versions are separated into different
* methods that are otherwise identical. (Similarly for siftDown.)
* These methods are static, with heap state as arguments, to
* simplify use in light of possible comparator exceptions.
*
* @param k 插入的目标位置
* @param x 待插入的元素
* @param array the heap array
*/
private static <T> void siftUpComparable(int k, T x, Object[] array) {
// 获取元素x实现的比较器
Comparable<? super T> key = (Comparable<? super T>) x;
while (k > 0) {
// 得到父节点所在位置, 公式为(k-1)/2
int parent = (k - 1) >>> 1;
// 父节点
Object e = array[parent];
// 比较是否待插入元素x的值大于父节点值,大于就说明符合堆要求
if (key.compareTo((T) e) >= 0)
break;
// 此时说明待插入元素x的值小于父节点值
// 就把父元素下放到当前位置k
array[k] = e;
// 从parent位置继续往上查找
k = parent;
}
// 当前元素放到正确的数组位置即可
array[k] = key;
}
3.7.2 siftUpUsingComparator
此方法是用指定的比较器,从下往上找元素应当放的位置,并调整沿途的元素位置
// 插入元素 x 到位置 k ,使用的是指定的比较器
// 查找方法其实和上面介绍的siftUpComparable方法相同
private static <T> void siftUpUsingComparator(int k, T x, Object[] array,
Comparator<? super T> cmp) {
while (k > 0) {
int parent = (k - 1) >>> 1;
Object e = array[parent];
if (cmp.compare(x, (T) e) >= 0)
break;
array[k] = e;
k = parent;
}
array[k] = x;
}
3.7.3 siftDownComparable
/**
* Inserts item x at position k, maintaining heap invariant by
* demoting x down the tree repeatedly until it is less than or
* equal to its children or is a leaf.
* 将元素x插入到位置k,并按堆的规则来调整堆
*
* @param k 插入元素的目标位置
* @param x 需要插入的元素
* @param array 堆数组
* @param n 堆大小
*/
private static <T> void siftDownComparable(int k, T x, Object[] array,
int n) {
if (n > 0) {
Comparable<? super T> key = (Comparable<? super T>)x;
int half = n >>> 1; // loop while a non-leaf
while (k < half) {
// k节点的左孩子
int child = (k << 1) + 1; // assume left child is least
Object c = array[child];
// 右孩子下标
int right = child + 1;
// 比较左右孩子较大的,让c指向较小的孩子,child指向其下标
if (right < n &&
((Comparable<? super T>) c).compareTo((T) array[right]) > 0)
// 此时左孩子大于右孩子的值
// 就让child指向右孩子下标,c指向右孩子对象,
c = array[child = right];
if (key.compareTo((T) c) <= 0)
// 比较插入元素的指和较小的孩子节点,
// 如果插入元素较小,就说明此时已经符合堆的规则,退出while循环
break;
// 否则就说明该元素比较小的孩子大,需要上移孩子节点,下移目标节点
// k位置指向较大的孩子,相当于上移孩子节点
array[k] = c;
// k指向孩子节点下标,相当于下移目标元素下标到原来较大的孩子节点下标处
k = child;
}
// 此时已经符合堆规则,将目标元素放到数组k位置即可
array[k] = key;
}
}
0x04 总结
以上分析了一些主要方法,其他方法大同小异就不再一一细讲。
其实PriorityBlockingQueue还是挺简单的,就是一个用数组实现的二叉小根堆来实现优先级队列。用了一个可重入锁ReentrantLock来再各个阶段进行阻塞的元素读取。