序列比对(十)——viterbi算法求解最可能路径

原创: hxj7

本文介绍了如何使用viterbi算法得到概率最大的路径。

前文《序列比对（九）从掷骰子说起HMM》已经通过投骰子的例子介绍了HMM的基本概念，引用如下：

那么如何通过已知的符号序列来预测未知的状态序列呢？我们将一串状态序列称为一条路径，那么如果要选择其中的一条路径作为预测结果, 也许我们该选择概率最大的，具体如下：

图片引自《生物序列分析》

其实，正如《序列比对（八）第一部分的小结》所说，后一状态依赖于前一个状态的问题很适合用动态规划算法解决。viterbi算法就是一种基于动态规划的求解最可能路径的算法。

更具体地，还以前文提到的掷骰子为例，当根据初始向量、转移矩阵、发射矩阵等参数生成一个随机的符号序列后，我们可以利用viterbi算法来求解最可能的路径。简单来讲，就是用viterbi算法来猜每次投掷用的是公平骰子还是作弊骰子。（如果对投骰子的例子不熟悉，请参考前文《序列比对（九）从掷骰子说起HMM》）

效果如下：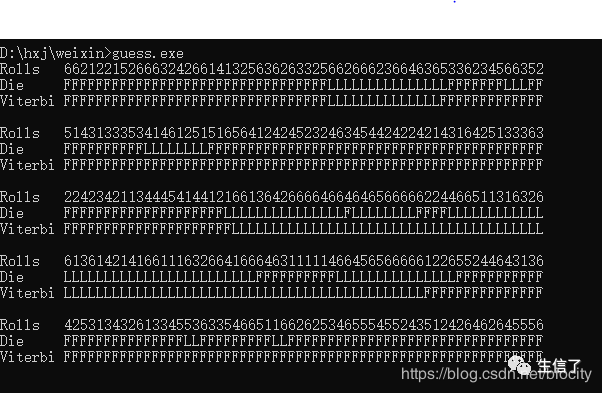
上图中Rolls代表300次投掷所产生的符号序列，Die表示投掷时实际所使用的骰子状态（F表示公平骰子，L表示作弊骰子），Viterbi表示利用viterbi算法求解的最可能路径。

具体代码如下：

（需要说明的是，实现viterbi算法要特别注意多个概率相乘会得到一个特别小的数，容易造成下溢，从而出错。所以我们将概率取log值，将公式中的概率相乘变成了log值的相加。）

#include 
#include 
#include 
#include 
#define MIN_LOG_VALUE -99

typedef char State;
typedef char Result;
State state[] = {'F', 'L'};   // 所有的可能状态
Result result[] = {'1', '2', '3', '4', '5', '6'};   // 所有的可能符号
double init[] = {0.9, 0.1};    // 初始状态的概率向量
double emission[][6] = {   // 发射矩阵：行对应着状态，列对应着符号
  1.0/6, 1.0/6, 1.0/6, 1.0/6, 1.0/6, 1.0/6,
  0.1, 0.1, 0.1, 0.1, 0.1, 0.5
};
double trans[][2] = {   // 转移矩阵：行和列都是状态
  0.95, 0.05,
  0.1, 0.9
};
const int nstate = 2;
const int nresult = 6;

State* rst;   // 一串随机状态序列
Result* rres;  // 一串随机符号序列
State* vst;   // viterbi算法猜出来的状态序列

struct Unit {
  double v;
  int *p;
  int size;
};
typedef struct Unit* pUnit;

int random(double* prob, const int n);
void randSeq(State* st, Result* res, const int n);
void printState(State* st, const int n);
void printResult(Result* res, const int n);
int getResultIndex(Result r);
void traceback(pUnit** a, const int l, const int i, State* st, const int m, int n);
void viterbi(Result* res, State* gst, const int n);

int main(void) {
  int i;
  int n = 300;
  if ((rst = (State*) malloc(sizeof(State) * n)) == NULL || \
      (rres = (Result*) malloc(sizeof(Result) * n)) == NULL || \
      (vst = (Result*) malloc(sizeof(Result) * n)) == NULL) {
    fputs("Error: out of space!\n", stderr);
    exit(1);
  }
  randSeq(rst, rres, n);
  viterbi(rres, vst, n);
  free(rst);
  free(rres);
  free(vst);
}

// 根据一个概率向量从0到n-1随机抽取一个数
int random(double* prob, const int n) {
  int i;
  double p = rand() / 1.0 / (RAND_MAX + 1);
  for (i = 0; i < n - 1; i++) {
    if (p <= prob[i])
      break;
    p -= prob[i];
  }
  return i;
}

// 根据转移矩阵和发射矩阵生成一串随机状态和符号
void randSeq(State* st, Result* res, const int n) {
  int i, ls, lr;
  srand((unsigned int) time(NULL));
  ls = random(init, nstate);
  lr = random(emission[ls], nresult);
  st[0] = state[ls];
  res[0] = result[lr];
  for (i = 1; i < n; i++) {
    ls = random(trans[ls], nstate);
    lr = random(emission[ls], nresult);
    st[i] = state[ls];
    res[i] = result[lr];
  }
}

void printState(State* st, const int n) {
  int i;
  for (i = 0; i < n; i++)
    printf("%c", st[i]);
  printf("\n");
}

void printResult(Result* res, const int n) {
  int i;
  for (i = 0; i < n; i++)
    printf("%c", res[i]);
  printf("\n");
}

int getResultIndex(Result r) {
  return r - result[0];
}

void traceback(pUnit** a, const int l, const int i, State* st, const int m, int n) {
  int j, k;
  int ll = 60;   // 每行打印几个元素
  int nl, nd;
  pUnit pu = a[l][i];
  if (! i) {
    st[n] = state[l];
    nl = m / ll;
    nd = m % ll;
    for (k = 0; k < nl; k++) {
      printf("Rolls\t");
      printResult(rres + k * ll, ll);
      printf("Die\t");
      printState(rst + k * ll, ll);
      printf("Viterbi\t");
      printState(st + k * ll, ll);
      printf("\n");
    }
    if (nd > 0) {
      printf("Rolls\t");
      printResult(rres + k * ll, nd);
      printf("Die\t");
      printState(rst + k * ll, nd);
      printf("Viterbi\t");
      printState(st + k * ll, nd);
      printf("\n"); 
    }
    printf("\n\n");
    return;  
  }
  st[n] = state[l];
  for (j = 0, k = 0; j < nstate && k < pu->size; j++) {
    if (pu->p[j]) {
      traceback(a, j, i - 1, st, m, n - 1);
      k++;
    }
  }
}

void viterbi(Result* res, State* gst, const int n) {
  double maxCol;
  double* tm;
  int i, j, k, l;
  int idx;
  pUnit** aUnit;  // 得分矩阵
  double* loginit;   // 每个元素都取log后的初始向量
  double** logem;  // 每个元素都取log后的发射矩阵
  double** logtrans;  // 每个元素都取log后的转移矩阵
  double v0 = 0;   // v0(0)的log值
  // 初始化
  if ((aUnit = (pUnit**) malloc(sizeof(pUnit*) * nstate)) == NULL || \
      (loginit = (double*) malloc(sizeof(double) * nstate)) == NULL || \
      (logem = (double**) malloc(sizeof(double*) * nstate)) == NULL || \
      (logtrans = (double**) malloc(sizeof(double*) * nstate)) == NULL) {
    fputs("Error: out of space!\n", stderr);
    exit(1);
  }
  for (i = 0; i < nstate; i++) {
    if ((aUnit[i] = (pUnit*) malloc(sizeof(pUnit) * n)) == NULL || \
        (logem[i] = (double*) malloc(sizeof(double) * nresult)) == NULL || \
        (logtrans[i] = (double*) malloc(sizeof(double) * nstate)) == NULL) {
      fputs("Error: out of space!\n", stderr);
      exit(1);
    }
    for (j = 0; j < n; j++) {
      if ((aUnit[i][j] = (pUnit) malloc(sizeof(struct Unit))) == NULL || \
          (aUnit[i][j]->p = (int*) malloc(sizeof(int) * nstate)) == NULL) {
        fputs("Error: out of space!\n", stderr);
        exit(1);
      }
      for (k = 0; k < nstate; k++)
        aUnit[i][j]->p[k] = 0;
      aUnit[i][j]->size = 0;
    }
  }
  if ((tm = (double*) malloc(sizeof(double) * nstate)) == NULL) {
    fputs("Error: out of space!\n", stderr);
    exit(1);    
  }
  // 初始向量取log值
  for (i = 0; i < nstate; i++)
    loginit[i] = init[i] == 0 ? MIN_LOG_VALUE : log(init[i]);
  // 发射矩阵取log值
  for (i = 0; i < nstate; i++)
    for (j = 0; j < nresult; j++)
      logem[i][j] = emission[i][j] == 0 ? MIN_LOG_VALUE : log(emission[i][j]);
  // 转移矩阵取log值
  for (i = 0; i < nstate; i++)
    for (j = 0; j < nstate; j++)
      logtrans[i][j] = trans[i][j] == 0 ? MIN_LOG_VALUE : log(trans[i][j]); 
  // 动态规划计算得分矩阵
  // 首先计算第0列，因为第0列的值和vk(0)有关
  // v0(0) = 1, vk(0) = 0 for k>0
  idx = getResultIndex(res[0]);
  for (l = 0; l < nstate; l++)
    aUnit[l][0]->v = v0 + loginit[l] + logem[l][idx];
  // 计算从第1列开始的各列
  for (i = 1; i < n; i++) {
    idx = getResultIndex(res[i]);
    for (l = 0; l < nstate; l++) {
      maxCol = tm[0] = aUnit[0][i - 1]->v + logtrans[0][l];
      for (k = 1; k < nstate; k++) {
        tm[k] = aUnit[k][i - 1]->v + logtrans[k][l];
        if (tm[k] > maxCol)
          maxCol = tm[k];
      }
      aUnit[l][i]->v = maxCol + logem[l][idx];
      for (k = 0; k < nstate; k++)
        if (tm[k] == maxCol) {
          aUnit[l][i]->p[k] = 1;
          aUnit[l][i]->size++;
        }
    }
  }
/*
  // 打印得分矩阵
  for (l = 0; l < nstate; l++) {
    for (i = 0; i < n; i++)
      printf("%f ", aUnit[l][i]->v);
    printf("\n");
  }
*/
  maxCol = aUnit[0][n - 1]->v;
  for (l = 1; l < nstate; l++)
    if (aUnit[l][n - 1]->v > maxCol)
      maxCol = aUnit[l][n - 1]->v;
  for (l = 0; l < nstate; l++)
    if (aUnit[l][n - 1]->v == maxCol) {
      traceback(aUnit, l, n - 1, gst, n, n - 1);
    }
}

(公众号：生信了)