牛客网左神算法中级班学习笔记(第四章)
本文是牛客网左神算法中级班学习笔记。

【分析】
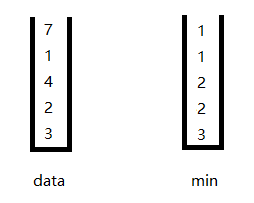
准备两个栈,一个栈是放数据的,另一个栈是放当前最小值的。
public static class MyStack2 {
private Stack<Integer> stackData;
private Stack<Integer> stackMin;
public MyStack2() {
this.stackData = new Stack<Integer>();
this.stackMin = new Stack<Integer>();
}
public void push(int newNum) {
if (this.stackMin.isEmpty()) {
this.stackMin.push(newNum);
} else if (newNum < this.getmin()) {
this.stackMin.push(newNum);
} else {
int newMin = this.stackMin.peek();
this.stackMin.push(newMin);
}
this.stackData.push(newNum);
}
public int pop() {
if (this.stackData.isEmpty()) {
throw new RuntimeException("Your stack is empty.");
}
this.stackMin.pop();
return this.stackData.pop();
}
public int getmin() {
if (this.stackMin.isEmpty()) {
throw new RuntimeException("Your stack is empty.");
}
return this.stackMin.peek();
}
}
public static class TwoQueuesStack {
private Queue<Integer> queue;
private Queue<Integer> help;
public TwoQueuesStack() {
queue = new LinkedList<Integer>();
help = new LinkedList<Integer>();
}
public void push(int pushInt) {
queue.add(pushInt);
}
public int peek() {
if (queue.isEmpty()) {
throw new RuntimeException("Stack is empty!");
}
while (queue.size() != 1) {
help.add(queue.poll());
}
int res = queue.poll();
help.add(res);
swap();
return res;
}
public int pop() {
if (queue.isEmpty()) {
throw new RuntimeException("Stack is empty!");
}
while (queue.size() > 1) {
help.add(queue.poll());
}
int res = queue.poll();
swap();
return res;
}
private void swap() {
Queue<Integer> tmp = help;
help = queue;
queue = tmp;
}
}
两个栈实现队列:
(准备两个栈,stackPop和stackPush,如果stackPop为空,才把stackPush的数据全部倒入stackPop栈中。)
public static class TwoStacksQueue {
private Stack<Integer> stackPush;
private Stack<Integer> stackPop;
public TwoStacksQueue() {
stackPush = new Stack<Integer>();
stackPop = new Stack<Integer>();
}
public void push(int pushInt) {
stackPush.push(pushInt);
}
public int poll() {
if (stackPop.empty() && stackPush.empty()) {
throw new RuntimeException("Queue is empty!");
} else if (stackPop.empty()) { // stackPop为空的时候,才把数据从stackPush栈倒入stackPop,一次倒完所有数据
while (!stackPush.empty()) {
stackPop.push(stackPush.pop());
}
}
return stackPop.pop();
}
public int peek() {
if (stackPop.empty() && stackPush.empty()) {
throw new RuntimeException("Queue is empty!");
} else if (stackPop.empty()) {
while (!stackPush.empty()) {
stackPop.push(stackPush.pop());
}
}
return stackPop.peek();
}
}

【分析】
总共情况种数:C(m+n, n) = C(m+n, m)。一共走m+n步,其中必有m步往右,必有n步往下。
动态规划思路:dp[i][j]表示从(i, j)到(n, m)位置的最短路径和,第一列和第一行仅取决于上一个,可以直接推出,其余各个位置仅仅取决于左边和上边,依次递推出。下面是动态规划(包括状态压缩版)和暴力递归的代码:
public class Main {
// 动态规划
public static int minPathSum1(int[][] m) {
if (m == null || m.length == 0 || m[0] == null || m[0].length == 0) {
return 0;
}
int row = m.length;
int col = m[0].length;
int[][] dp = new int[row][col];
dp[0][0] = m[0][0];
for (int i = 1; i < row; i++) {
dp[i][0] = dp[i - 1][0] + m[i][0];
}
for (int j = 1; j < col; j++) {
dp[0][j] = dp[0][j - 1] + m[0][j];
}
for (int i = 1; i < row; i++) {
for (int j = 1; j < col; j++) {
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + m[i][j];
}
}
return dp[row - 1][col - 1];
}
// 动态规划(状态压缩)---选择行列较小的值作为一维数组的长度进行状态压缩
public static int minPathSum2(int[][] m) {
if (m == null || m.length == 0 || m[0] == null || m[0].length == 0) {
return 0;
}
int more = Math.max(m.length, m[0].length);
int less = Math.min(m.length, m[0].length);
boolean rowmore = more == m.length;
int[] arr = new int[less];
arr[0] = m[0][0];
for (int i = 1; i < less; i++) {
arr[i] = arr[i - 1] + (rowmore ? m[0][i] : m[i][0]);
}
for (int i = 1; i < more; i++) {
arr[0] = arr[0] + (rowmore ? m[i][0] : m[0][i]);
for (int j = 1; j < less; j++) {
arr[j] = Math.min(arr[j - 1], arr[j])
+ (rowmore ? m[i][j] : m[j][i]);
}
}
return arr[less - 1];
}
// 暴力递归
public static int minPathSum3(int[][] m){
if (m == null || m.length == 0 || m[0] == null || m[0].length == 0) {
return 0;
}
return process(m, 0, 0);
}
public static int process(int[][] m, int x, int y){
if(x >= m.length || y >= m[0].length){
return Integer.MAX_VALUE;
}
if(x == m.length-1 && y == m[0].length-1){
return m[x][y];
}
return m[x][y] + Math.min(process(m, x+1, y), process(m, x, y+1));
}
// for test
public static int[][] generateRandomMatrix(int rowSize, int colSize) {
if (rowSize < 0 || colSize < 0) {
return null;
}
int[][] result = new int[rowSize][colSize];
for (int i = 0; i != result.length; i++) {
for (int j = 0; j != result[0].length; j++) {
result[i][j] = (int) (Math.random() * 10);
}
}
return result;
}
// for test
public static void printMatrix(int[][] matrix) {
for (int i = 0; i != matrix.length; i++) {
for (int j = 0; j != matrix[0].length; j++) {
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
}
public static void main(String[] args) {
for(int i = 0; i < 500000; i++){
int[][] m = generateRandomMatrix(3, 4);
int res1 = minPathSum1(m);
int res2 = minPathSum2(m);
int res3 = minPathSum3(m);
if(res1 != res3){
printMatrix(m);
System.out.println(minPathSum1(m));
System.out.println(minPathSum3(m));
return;
}
if(res1 != res2){
printMatrix(m);
System.out.println(minPathSum1(m));
System.out.println(minPathSum2(m));
return;
}
if(res2 != res3){
printMatrix(m);
System.out.println(minPathSum2(m));
System.out.println(minPathSum3(m));
return;
}
}
System.out.println("true");
}
}

【分析】
这个题如果依次统计每个波谷的水量就入坑了。。。如左老师所说如下图:
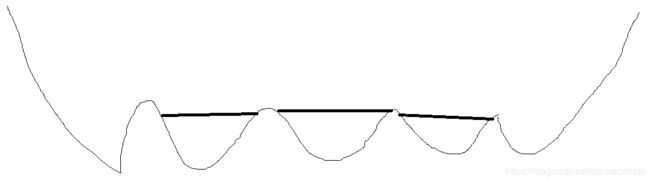
如果仅仅统计那些波谷,但两头忽然都上去了,那中间就白统计了。。。
正确的思路是,仅仅考虑每个柱子能留存的水量,每个柱子能留存的水量,就是该柱子左边所有柱子的最大值和右边所有柱子的最大值中的较大值减去该柱子的值(前提是左边最大和右边最大都比该柱子大才有留存水的可能)。
// 暴力求解
public static int getWater1(int[] arr) {
if (arr == null || arr.length < 3) {
return 0;
}
int value = 0;
for (int i = 1; i < arr.length - 1; i++) {
int leftMax = 0;
int rightMax = 0;
for (int l = 0; l < i; l++) {
leftMax = Math.max(arr[l], leftMax);
}
for (int r = i + 1; r < arr.length; r++) {
rightMax = Math.max(arr[r], rightMax);
}
value += Math.max(0, Math.min(leftMax, rightMax) - arr[i]);
}
return value;
}
// 预处理优化
public static int getWater2(int[] arr) {
if (arr == null || arr.length < 3) {
return 0;
}
int n = arr.length;
int[] leftMaxs = new int[n];
leftMaxs[0] = 0;
for (int i = 1; i < n; i++) {
leftMaxs[i] = Math.max(leftMaxs[i - 1], arr[i-1]);
}
int[] rightMaxs = new int[n];
rightMaxs[n - 1] = 0;
for (int i = n - 2; i >= 0; i--) {
rightMaxs[i] = Math.max(rightMaxs[i + 1], arr[i + 1]);
}
int value = 0;
for (int i = 0; i < n; i++) {
value += Math.max(0, Math.min(leftMaxs[i], rightMaxs[i]) - arr[i]);
}
return value;
}
// 从左向右结算,可以用一个leftMax变量代替leftMaxs数组
public static int getWater3(int[] arr) {
if (arr == null || arr.length < 3) {
return 0;
}
int n = arr.length;
int[] rightMaxs = new int[n];
rightMaxs[n - 1] = 0;
for (int i = n - 2; i >= 0; i--) {
rightMaxs[i] = Math.max(rightMaxs[i + 1], arr[i + 1]);
}
int leftMax = arr[0];
int value = 0;
for (int i = 1; i < n; i++) {
value += Math.max(0, Math.min(leftMax, rightMaxs[i]) - arr[i]);
leftMax = Math.max(leftMax, arr[i]);
}
return value;
}
// 双指针优化。其实相当于从左右两边同时结算,左右leftMax和rightMax代替了左右两个预处理数组
public static int getWater4(int[] arr) {
if (arr == null || arr.length < 3) {
return 0;
}
int value = 0;
int leftMax = arr[0];
int rightMax = arr[arr.length - 1];
int l = 1;
int r = arr.length - 2;
while (l <= r) {
if (leftMax <= rightMax) {
value += Math.max(0, leftMax - arr[l]);
leftMax = Math.max(leftMax, arr[l++]);
} else {
value += Math.max(0, rightMax - arr[r]);
rightMax = Math.max(rightMax, arr[r--]);
}
}
return value;
}

【分析】
判断a是否和b互为旋转字符串,只需要把其中一个比如a=a+a;然后判定b是否是a的子串即可。下面判定子串用到了KMP算法,具体参看链接。
public static boolean isRotation(String a, String b) {
if (a == null || b == null || a.length() != b.length()) {
return false;
}
String b2 = b + b;
return getIndexOf(b2, a) != -1; // return b2.indexOf(a) != -1;
}
// KMP Algorithm
public static int getIndexOf(String s, String m) {
if (s.length() < m.length()) {
return -1;
}
char[] ss = s.toCharArray();
char[] ms = m.toCharArray();
int si = 0;
int mi = 0;
int[] next = getNextArray(ms);
while (si < ss.length && mi < ms.length) {
if (ss[si] == ms[mi]) {
si++;
mi++;
} else if (next[mi] == -1) {
si++;
} else {
mi = next[mi];
}
}
return mi == ms.length ? si - mi : -1;
}
public static int[] getNextArray(char[] ms) {
if (ms.length == 1) {
return new int[] { -1 };
}
int[] next = new int[ms.length];
next[0] = -1;
next[1] = 0;
int pos = 2;
int cn = 0;
while (pos < next.length) {
if (ms[pos - 1] == ms[cn]) {
next[pos++] = ++cn;
} else if (cn > 0) {
cn = next[cn];
} else {
next[pos++] = 0;
}
}
return next;
}

【分析】
根据题意,左部分必定至少包含第一个元素,右部分至少包含最后一个元素。先求出全局最大值max,可以把max划到左部分或者右部分,为了使得最终所求值最大,那就尽量使得max不在的那部分的最大值尽可能的小,又由于至少含有一个元素,那就让max不在的那部分就只含有一个元素吧!!
public static int maxABS3(int[] arr) {
int max = Integer.MIN_VALUE;
for (int i = 0; i < arr.length; i++) {
max = Math.max(arr[i], max);
}
return max - Math.min(arr[0], arr[arr.length - 1]);
}