从程序员角度分析2004年数学建模b题
整个7月份去了美国嗨了半多个月,现在才开始和队友一起备赛,真是罪过罪过.....
做了几道题目后觉得数学建模的一些知识点比较琐碎(从编程的角度),尤其是数据处理方面,所以给自己写个总结,主要是给自己回头翻找的,欢迎指正哈~~
所有的数学建模题目和数据均可以在http://www.mcm.edu.cn/的赛题与评奖中的以前竞赛赛题中下载
一般来说数学建模会有两道题目,一道是侧重于计算方面的,说白了就是实打实地建立模型,编程求解数值,一般这种题目的结果还确定,然后最后一问可能会让你自由发挥扩展,结果就各不相同了,另一种是侧重于数据分析的,比如让你分析医改怎么样之类的,公说公有理婆说婆有理,这个就比较靠脑洞了。我们主要训练的是第一种,毕竟都是理科生嘛。
2004年b题难度主要在于读懂题目:
1,8个机组出力值和6条线路潮流值是什么关系.
2,如何由各个机组的段容量确定各自的段价.
3,如何由段价算出清算价
4,读懂输电阻塞管理原则(即先避免各线路超出规定的潮流值,如果不行则防止超过安全裕度,最后实在不行则直接拉闸)
先看第一问:
试用这些数据确定各线路上有功潮流关于各发电机组出力的近似表达式。
赤裸裸的数据拟合,自变量是各机组的出力值,因变量是各线路的有功潮流值,这里需要注意8个机组确定6条线路,但是6条线路的关系式肯定各不相同,所以拟合6次.
拟合的方式在之前的博客写的很清楚http://blog.csdn.net/fengsigaoju/article/details/51100402和http://blog.csdn.net/fengsigaoju/article/details/51025195。
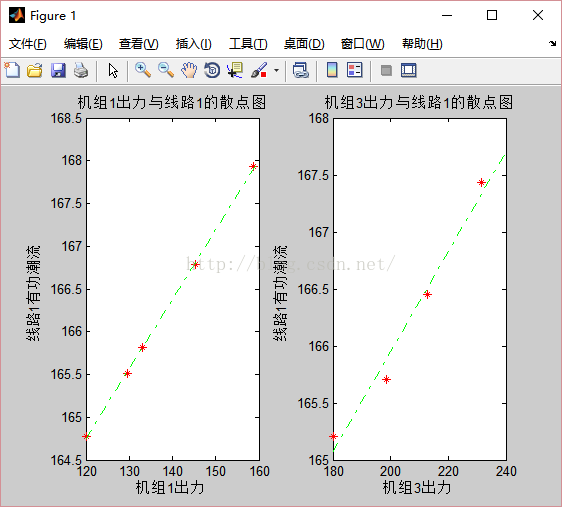
在我们不清楚它们之间的关系时先考虑线性(当然最好是画个散点图说明),发现结果很不错就行了.
散点图代码(这里还把拟合的线给画出来了,可以省略):
clear all
clc
y=xlsread('problem three.xls','A1:A5');
x=xlsread('problem two.xls','A1:A5');
subplot(1,2,1);
plot(x,y,'r*');
t=[ones(5,1),x];
b=regress(y,t);
x1=120:160;
y1=b(1)+x1*b(2);
hold on
plot(x1,y1,'g-.');
xlabel('机组1出力');
ylabel('线路1有功潮流');
title('机组1出力与线路1的散点图');
subplot(1,2,2);
x=xlsread('problem two.xls','C9:C12');
y=xlsread('problem three.xls','A9:A12');
plot(x,y,'r*');
t=[ones(4,1),x];
b=regress(y,t);
x2=180:240;
y2=b(1)+b(2)*x2;
hold on
plot(x2,y2,'g-.');
xlabel('机组3出力');
ylabel('线路1有功潮流');
title('机组3出力与线路1的散点图');
第二问是自己设计,跳过。
第三问:试按照电力市场规则给出下一个时段各机组的出力分配预案。
也就是给定总出力值,不考虑潮流值的情况下,只考虑价格求最省钱的各机组处理分配方案。
计算最大段价的步骤如下:
step1:先根据当前出力和爬坡速率求出下一时段每个机组的出力范围.
step2:根据当前的出力范围划出当前各个机组的能够取到的段容量.
step3:在当前符合的段容量所对应的段价中找到最大值,并计算其所对应的段容与其余机组可以取得的最大段容量之和,若和大于984.2则跳转4,否则跳转5
step4:在该机组的可供选择的段容中删去该最大值所对应的段容,并更新当前最大段价,跳转3.
step5:最大段价为之前所记录的最大值.
得到每一个机组出力值的步骤如下:
step1:首先获得之前计算最大段价时最后得到的符合段容量.
step2:除去取得最大段价那个机组外,每一个机组的出力值均取当前范围内的最大容量并计算和.
step3:用984.2减去之前计算的和即为剩余那个机组的出力值.
clear
t=input('请输入总出力值:');
base=xlsread('problem two.xls','A1:H1');
speed=[2.2 1 3.2 1.3 1.8 2 1.4 1.8];
c=[];
for i=1:size(speed,2)
c=[c,base(1,i)+15*speed(1,i)];
end
%第一步先算出15分钟后每个机组的最大出力值
x=xlsread('problem four.xls','A1:J8');
a=[];
for i=1:size(x,1)
sum=0;
for j=1:size(x,2)
sum=sum+x(i,j);
if sum>c(1,i)
break;
end
end
a=[a,j];
end
%根据最大出力值画出各机组段容量的范围
y=xlsread('problem five.xls','A1:J8');
true=0;
while(true==0)
max=0;
for i=1:8
for j=1:a(1,i)
if y(i,j)>max
max=y(i,j);
step=i;
step2=j;%找到当前最大值以及其所在的行和列
end
end
end
sum=0;
for i=1:8
if (step==i)
for j=1:step2
sum=sum+x(i,j);
end
else
for j=1:a(1,i)
sum=sum+x(i,j);
end
end
end%记录此时表3的最大出力和与982.4比较
if sum>=t
answer=max;%记录下当前的最大值
a(1,step)=step2-1;
step3=step;%记下最大值所在的行与列
step4=step2;
else
true=1;
end
end
%answer就是清算值而a里面存储的是下一次的,也就是说下一次+到清算值对应的表3就是安排方案
disp(['清算价格为:',num2str(answer)]);
p=[];
value=0;
for i=1:8
sum=0;
if (i~=step3)
for j=1:a(1,i)%其余的行并没有扩展
sum=sum+x(i,j);
end
if sum>c(1,i)
sum=c(1,i);%注意此处,有可能之前的出力是可以满足的最后一个
end
p(1,i)=sum;
value=value+sum;
end
end
p(1,step3)=t-value;
disp(['出力值为:',num2str(p)]);问题的难点在于阻塞费用的计算是一个分段函数,而分段函数是无法直接用软件求解的。
所以分解成一个个子问题分别求出在该范围内的最大阻塞费用,最后比较取最大值。
这里边用到fmincon,fmincon无法传递函数值进去,所以可以设计大于等于的值为全局变量。
clear;
y=xlsread('problem four.xls','A1:J8');
r=xlsread('problem five.xls','A1:J8');
safe=[165 150 160 155 132 162];
d=[173.3047 141.0049 -150.9235 120.9114 136.8265 168.519];
x=[120 73 180 80 125 125 81.1 90];
speed=[2.2 1 3.2 1.3 1.8 2 1.4 1.8];
p=[];%上界
q=[];%下界
for i=1:8
p=[p x(1,i)+speed(1,i)*15];
q=[q x(1,i)-speed(1,i)*15];
end
answer=[];
for i=1:8
sum=0;
t=0;
for j=1:10
sum=sum+y(i,j);
if sum>=q(1,i) && t==0%第一次找到
answer(i,1)=j;
t=2;
continue;
end
if sum<=p(1,i) && t~=0
answer(i,t)=j;
t=t+1;
end
if sum>p(1,i)
answer(i,t)=j;
break;
end
end
end
z=[];
for i=1:8
sum=0;
for j=1:8
if answer(i,j)~=0
sum=sum+1;
else
break;
end
end
z=[z,sum];
end
ma=1000000;
Ma=1000000;
options=optimset;
for d1=7:7
for d2=6:6
for d3=5:5
for d4=1:(z(1,4)-1)
for d5=5:(z(1,5)-1)
for d6=1:(z(1,6)-1)
for d7=2:(z(1,7)-1)
for d8=1:(z(1,8)-1)
global t;
t=[];
m=[];
sum=0;
for i=1:answer(1,d1)
sum=sum+y(1,i);
end
t=[t,sum,sum+y(1,answer(1,d1+1))];
m=[m,r(1,d1+1)];
sum=0;
for i=1:answer(2,d2)
sum=sum+y(2,i);
end
t=[t,sum,sum+y(2,answer(2,d2+1))];
m=[m,r(2,d2+1)];
%%%%%%%%%%%%%%%%%%
sum=0;
for i=1:answer(3,d3)
sum=sum+y(3,i);
end
t=[t,sum,sum+y(3,answer(3,d3+1))];
m=[m,r(3,d3+1)];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
sum=0;
for i=1:answer(4,d4)
sum=sum+y(4,i);
end
t=[t,sum,sum+y(4,answer(4,d4+1))];
m=[m,r(4,d4+1)];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%
sum=0;
for i=1:answer(5,d5)
sum=sum+y(5,i);
end
t=[t,sum,sum+y(5,answer(5,d5+1))];
m=[m,r(5,d5+1)];
%%%%%%%%%%%%%%%%%%%%%%%%%%
sum=0;
for i=1:answer(6,d6)
sum=sum+y(6,i);
end
t=[t,sum,sum+y(6,answer(6,d6+1))];
m=[m,r(6,d6+1)];
%%%%%%%%%%%%%%%%%%%%%%%%%%
sum=0;
for i=1:answer(7,d7)
sum=sum+y(7,i);
end
t=[t,sum,sum+y(7,answer(7,d7+1))];
m=[m,r(7,d7+1)];
%%%%%%%%%%%%%%%%%%%%%%
sum=0;
for i=1:answer(8,d8)
sum=sum+y(8,i);
end
t=[t,sum,sum+y(8,answer(8,d8+1))];
m=[m,r(8,d8+1)];
%接下去找段价最高
t=[t,max(m)];
max(m);
sum=0;
for i=1:16
sum=sum+t(i);
end
t(7)
t(8)
if (sum>=982.4)
[x,l]=fmincon('fun55',rand(8,1),[],[],[],[],zeros(8,1),[],'mycon2',options)
y1=110.4775+0.0826*x(1)+0.0478*x(2)+0.0528*x(3)+0.1199*x(4)-0.0257*x(5)+0.1216*x(6)+0.1220*x(7)-0.0015*x(8)
y2=131.3521-0.0547*x(1)+0.1275*x(2)-0.0001*x(3)+0.0332*x(4)+0.0867*x(5)-0.1127*x(6)-0.0186*x(7)+0.0985*x(8)
y3=abs(-108.9928-0.0694*x(1)+0.0620*x(2)-0.1565*x(3)-0.0099*x(4)+0.1247*x(5)+0.0024*x(6)-0.0028*x(7)-0.2012*x(8))
y4=77.6116-0.0346*x(1)-0.1028*x(2)+0.2050*x(3)-0.0209*x(4)-0.0120*x(5)+0.0057*x(6)+0.1452*x(7)+0.0763*x(8)
y5=133.1334+0.003*x(1)+0.2428*x(2)-0.0647*x(3)-0.0412*x(4)-0.0655*x(5)+0.070*x(6)-0.0039*x(7)-0.0092*x(8)
y6=120.8481+0.2376*x(1)-0.0607*x(2)-0.0781*x(3)+0.0929*x(4)+0.0466*x(5)-0.0003*x(6)+0.1664*x(7)+0.0004*x(8)
if y1<=165&&y2<=150&&y3<=160&&y4<=155&&y5<=132&&y6<=162&&lfun55.m
function f=fun55(x)
global t;
%z=[(110.4775+.0826*x(1)+0.0478*x(2)+0.0528*x(3)+0.1199*x(4)-0.0257*x(5)+0.1216*x(6)+0.1220*x(7)-0.0015*x(8)-165)/165,(131.3521-0.0547*x(1)+0.1275*x(2)-0.0001*x(3)+0.0332*x(4)+0.0867*x(5)-0.1127*x(6)-0.0186*x(7)+0.0985*x(8)-150)/150,(abs(-108.9928-0.0694*x(1)+0.0620*x(2)-0.1565*x(3)-0.0099*x(4)+0.1247*x(5)+0.0024*x(6)-0.0028*x(7)-0.2012*x(8))-160)/160,(77.6116-0.0346*x(1)-0.1028*x(2)+0.2050*x(3)-0.0209*x(4)-0.0120*x(5)+0.0057*x(6)+0.1452*x(7)+0.0763*x(8)-155)/155,(133.1334+0.003*x(1)+0.2428*x(2)-0.0647*x(3)-0.0412*x(4)-0.0655*x(5)+0.070*x(6)-0.0039*x(7)-0.0092*x(8)-132)/132,(120.8481+0.2376*x(1)-0.0607*x(2)-0.0781*x(3)+0.0929*x(4)+0.0466*x(5)-0.0003*x(6)+0.1664*x(7)+0.0004*x(8)-162)/162];
f=(x(1)-120)+(x(2)-73)+(x(3)-180)+(x(4)-80)+(x(5)-125)+(x(6)-125)+(x(7)-81.1)+(x(8)-90)*t(17);mycon2.m
function[g,ceg]=mycon2(x)
global t;
g(1)=x(1)-t(2);
g(2)=x(2)-t(4);
g(3)=t(1)-x(1);
g(4)=t(3)-x(2);
g(5)=t(5)-x(3);
g(6)=x(3)-t(6);
g(7)=t(7)-x(4);
g(8)=x(4)-t(8);
g(9)=t(9)-x(5);
g(10)=x(5)-t(10);
g(11)=t(11)-x(6);
g(12)=x(6)-t(12);
g(13)=t(13)-x(7);
g(14)=x(7)-t(14);
g(15)=t(15)-x(8);
g(16)=x(8)-t(16);
g(17)=110.4775+0.0826*x(1)+0.0478*x(2)+0.0528*x(3)+0.1199*x(4)-0.0257*x(5)+0.1216*x(6)+0.1220*x(7)-0.0015*x(8)-186.45;
g(18)=131.3521-0.0547*x(1)+0.1275*x(2)-0.0001*x(3)+0.0332*x(4)+0.0867*x(5)-0.1127*x(6)-0.0186*x(7)+0.0985*x(8)-177;
g(19)=abs(-108.9928-0.0694*x(1)+0.0620*x(2)-0.1565*x(3)-0.0099*x(4)+0.1247*x(5)+0.0024*x(6)-0.0028*x(7)-0.2012*x(8))-174.4;
g(20)=77.6116-0.0346*x(1)-0.1028*x(2)+0.2050*x(3)-0.0209*x(4)-0.0120*x(5)+0.0057*x(6)+0.1452*x(7)+0.0763*x(8)-172.05;
g(21)=133.1334+0.003*x(1)+0.2428*x(2)-0.0647*x(3)-0.0412*x(4)-0.0655*x(5)+0.070*x(6)-0.0039*x(7)-0.0092*x(8)-151.80;
g(22)=120.8481+0.2376*x(1)-0.0607*x(2)-0.0781*x(3)+0.0929*x(4)+0.0466*x(5)-0.0003*x(6)+0.1664*x(7)+0.0004*x(8)-184.68;
g(23)=x(1)-153;
g(24)=x(2)-88;
g(25)=x(3)-228;
g(26)=x(4)-99.5;
g(27)=x(5)-152;
g(28)=x(6)-155;
g(29)=x(7)-102;
g(30)=x(8)-117;
ceg=x(1)+x(2)+x(3)+x(4)+x(5)+x(6)+x(7)+x(8)-982.4;而第五问带入这个式子计算发现找不到最优解,说明不可能在满足规定值的情况下做到满足负荷需求,所以将规定值修改为安全裕度.
而此时要安全与费用并重,这就是一个多目标规划问题,而多目标规划问题通常加权转化为单目标规划问题。
fun44.m
function f=fun44(x)
global t;
z=[(110.4775+.0826*x(1)+0.0478*x(2)+0.0528*x(3)+0.1199*x(4)-0.0257*x(5)+0.1216*x(6)+0.1220*x(7)-0.0015*x(8)-165)/165,(131.3521-0.0547*x(1)+0.1275*x(2)-0.0001*x(3)+0.0332*x(4)+0.0867*x(5)-0.1127*x(6)-0.0186*x(7)+0.0985*x(8)-150)/150,(abs(-108.9928-0.0694*x(1)+0.0620*x(2)-0.1565*x(3)-0.0099*x(4)+0.1247*x(5)+0.0024*x(6)-0.0028*x(7)-0.2012*x(8))-160)/160,(77.6116-0.0346*x(1)-0.1028*x(2)+0.2050*x(3)-0.0209*x(4)-0.0120*x(5)+0.0057*x(6)+0.1452*x(7)+0.0763*x(8)-155)/155,(133.1334+0.003*x(1)+0.2428*x(2)-0.0647*x(3)-0.0412*x(4)-0.0655*x(5)+0.070*x(6)-0.0039*x(7)-0.0092*x(8)-132)/132,(120.8481+0.2376*x(1)-0.0607*x(2)-0.0781*x(3)+0.0929*x(4)+0.0466*x(5)-0.0003*x(6)+0.1664*x(7)+0.0004*x(8)-162)/162];
f=0.5*max(z)+0.5*((x(1)-120)+(x(2)-73)+(x(3)-180)+(x(4)-80)+(x(5)-125)+(x(6)-125)+(x(7)-81.1)+(x(8)-90))*t(17)/374796.8;mycon2.m
function[g,ceg]=mycon2(x)
global t;
g(1)=x(1)-t(2);
g(2)=x(2)-t(4);
g(3)=t(1)-x(1);
g(4)=t(3)-x(2);
g(5)=t(5)-x(3);
g(6)=x(3)-t(6);
g(7)=t(7)-x(4);
g(8)=x(4)-t(8);
g(9)=t(9)-x(5);
g(10)=x(5)-t(10);
g(11)=t(11)-x(6);
g(12)=x(6)-t(12);
g(13)=t(13)-x(7);
g(14)=x(7)-t(14);
g(15)=t(15)-x(8);
g(16)=x(8)-t(16);
g(17)=110.4775+0.0826*x(1)+0.0478*x(2)+0.0528*x(3)+0.1199*x(4)-0.0257*x(5)+0.1216*x(6)+0.1220*x(7)-0.0015*x(8)-186.45;
g(18)=131.3521-0.0547*x(1)+0.1275*x(2)-0.0001*x(3)+0.0332*x(4)+0.0867*x(5)-0.1127*x(6)-0.0186*x(7)+0.0985*x(8)-177;
g(19)=abs(-108.9928-0.0694*x(1)+0.0620*x(2)-0.1565*x(3)-0.0099*x(4)+0.1247*x(5)+0.0024*x(6)-0.0028*x(7)-0.2012*x(8))-174.4;
g(20)=77.6116-0.0346*x(1)-0.1028*x(2)+0.2050*x(3)-0.0209*x(4)-0.0120*x(5)+0.0057*x(6)+0.1452*x(7)+0.0763*x(8)-172.05;
g(21)=133.1334+0.003*x(1)+0.2428*x(2)-0.0647*x(3)-0.0412*x(4)-0.0655*x(5)+0.070*x(6)-0.0039*x(7)-0.0092*x(8)-151.80;
g(22)=120.8481+0.2376*x(1)-0.0607*x(2)-0.0781*x(3)+0.0929*x(4)+0.0466*x(5)-0.0003*x(6)+0.1664*x(7)+0.0004*x(8)-184.68;
g(23)=x(1)-153;
g(24)=x(2)-88;
g(25)=x(3)-228;
g(26)=x(4)-99.5;
g(27)=x(5)-152;
g(28)=x(6)-155;
g(29)=x(7)-102;
g(30)=x(8)-117;
ceg=x(1)+x(2)+x(3)+x(4)+x(5)+x(6)+x(7)+x(8)-1052.8;five.m
clear;
y=xlsread('problem four.xls','A1:J8');
r=xlsread('problem five.xls','A1:J8');
safe=[186.45 177 174.4 172.05 151.80 184.68];
d=[173.3047 141.0049 -150.9235 120.9114 136.8265 168.519];
x=[120 73 180 80 125 125 81.1 90];
speed=[2.2 1 3.2 1.3 1.8 2 1.4 1.8];
p=[];%上界
q=[];%下界
for i=1:8
p=[p x(1,i)+speed(1,i)*15];
q=[q x(1,i)-speed(1,i)*15];
end
answer=[];
for i=1:8
sum=0;
t=0;
for j=1:10
sum=sum+y(i,j);
if sum>=q(1,i) && t==0%第一次找到
answer(i,1)=j;
t=2;
continue;
end
if sum<=p(1,i) && t~=0
answer(i,t)=j;
t=t+1;
end
if sum>p(1,i)
answer(i,t)=j;
break;
end
end
end
z=[];
for i=1:8
sum=0;
for j=1:8
if answer(i,j)~=0
sum=sum+1;
else
break;
end
end
z=[z,sum];
end
ma=1000000;
Ma=1000000;
options=optimset;
for d1=7:7
for d2=1:(z(1,1)-1)
for d3=1:(z(1,1)-1)
for d4=1:(z(1,4)-1)
for d5=5:(z(1,5)-1)
for d6=1:(z(1,6)-1)
for d7=2:(z(1,7)-1)
for d8=1:(z(1,8)-1)
global t;
t=[];
m=[];
sum=0;
for i=1:answer(1,d1)
sum=sum+y(1,i);
end
t=[t,sum,sum+y(1,answer(1,d1+1))];
m=[m,r(1,d1+1)];
sum=0;
for i=1:answer(2,d2)
sum=sum+y(2,i);
end
t=[t,sum,sum+y(2,answer(2,d2+1))];
m=[m,r(2,d2+1)];
%%%%%%%%%%%%%%%%%%
sum=0;
for i=1:answer(3,d3)
sum=sum+y(3,i);
end
t=[t,sum,sum+y(3,answer(3,d3+1))];
m=[m,r(3,d3+1)];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
sum=0;
for i=1:answer(4,d4)
sum=sum+y(4,i);
end
t=[t,sum,sum+y(4,answer(4,d4+1))];
m=[m,r(4,d4+1)];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%
sum=0;
for i=1:answer(5,d5)
sum=sum+y(5,i);
end
t=[t,sum,sum+y(5,answer(5,d5+1))];
m=[m,r(5,d5+1)];
%%%%%%%%%%%%%%%%%%%%%%%%%%
sum=0;
for i=1:answer(6,d6)
sum=sum+y(6,i);
end
t=[t,sum,sum+y(6,answer(6,d6+1))];
m=[m,r(6,d6+1)];
%%%%%%%%%%%%%%%%%%%%%%%%%%
sum=0;
for i=1:answer(7,d7)
sum=sum+y(7,i);
end
t=[t,sum,sum+y(7,answer(7,d7+1))];
m=[m,r(7,d7+1)];
%%%%%%%%%%%%%%%%%%%%%%
sum=0;
for i=1:answer(8,d8)
sum=sum+y(8,i);
end
t=[t,sum,sum+y(8,answer(8,d8+1))];
m=[m,r(8,d8+1)];
%接下去找段价最高
t=[t,max(m)];
max(m);
sum=0;
for i=1:16
sum=sum+t(i);
end
if (sum>=1052.8)
[x,l]=fmincon('fun44',rand(8,1),[],[],[],[],zeros(8,1),[],'mycon2',options)
y1=110.4775+0.0826*x(1)+0.0478*x(2)+0.0528*x(3)+0.1199*x(4)-0.0257*x(5)+0.1216*x(6)+0.1220*x(7)-0.0015*x(8)
y2=131.3521-0.0547*x(1)+0.1275*x(2)-0.0001*x(3)+0.0332*x(4)+0.0867*x(5)-0.1127*x(6)-0.0186*x(7)+0.0985*x(8)
y3=abs(-108.9928-0.0694*x(1)+0.0620*x(2)-0.1565*x(3)-0.0099*x(4)+0.1247*x(5)+0.0024*x(6)-0.0028*x(7)-0.2012*x(8))
y4=77.6116-0.0346*x(1)-0.1028*x(2)+0.2050*x(3)-0.0209*x(4)-0.0120*x(5)+0.0057*x(6)+0.1452*x(7)+0.0763*x(8)
y5=133.1334+0.003*x(1)+0.2428*x(2)-0.0647*x(3)-0.0412*x(4)-0.0655*x(5)+0.070*x(6)-0.0039*x(7)-0.0092*x(8)
y6=120.8481+0.2376*x(1)-0.0607*x(2)-0.0781*x(3)+0.0929*x(4)+0.0466*x(5)-0.0003*x(6)+0.1664*x(7)+0.0004*x(8)
if l这道题目层次鲜明,线性回归(1),贪心法求解无约束条件的规划问题(3),单目标规划(4),代入第五问发现无解故用到另一个多目标规划的模型(5)