代码本色 结合牛顿力学

目录
序章 随机游走
第一章 向量
第二章 力
第三章 震荡
第四章 粒子系统
序章 随机游走
1.借以回顾本书的中心编程思想——面向对象编程。我们要用面向对象方法来模拟物体在 Processing窗口的运动，随机游走模型就是这个例子的模板。
2.随机游走模型引入了贯穿本书的两个关键问题：如何定义对象的行为规则，以及如何用 Processing模拟这些行为规则。
3.在本书中，我们需要对随机性、概率和Perlin噪声有基本的了解，随机游走模型展示了 其中的关键点，这在我们以后的学习中会很有用。
Perlin噪声
Perlin噪声算法表现出了一定的自然性，因为它能生成符合自然排序（“平滑”）的伪随机 数序列。图I-5展示了Perlin噪声的效果，x轴代表时间；请注意曲线的平滑性。
调整由Perlin噪声功能产生的细节的特征和水平。 类似于物理学中的谐波，噪声是在几个八度计算的。 较低的八度对输出信号贡献更大，因此定义噪声的过强度，而较高的八度将噪声序列中的细节细化。
默认情况下，噪声计算超过4个八度音阶，每个八度音阶的贡献与其前身的比例相差一倍，从第一个八度音阶的50％强度开始。 可以通过添加附加的功能参数来改变该衰减量。
通过改变这些参数，由noise（）函数创建的信号可以适应非常特定的需求和特性。

```java
float noiseVal;
float noiseScale=0.02;

void draw() {
for (int y = 0; y < height; y++) {
for (int x = 0; x < width/2; x++) {
noiseDetail(3,0.5);
noiseVal = noise((mouseX+x) * noiseScale, (mouseY+y) * noiseScale);
stroke(noiseVal*255);
point(x,y);
noiseDetail(8,0.65);
noiseVal = noise((mouseX + x + width/2) * noiseScale,
(mouseY + y) * noiseScale);
stroke(noiseVal * 255);
point(x + width/2, y);
}
}
}

![在这里插入图片描述](https://img-blog.csdnimg.cn/20200104181842684.gif)
**第一章向量**

小球向鼠标方向移动
我们可以将其看成两个不同方向单位矢量的合成
)
```java
class Mover {    
  // The Mover tracks position, velocity, and acceleration  
PVector position;  
PVector velocity; 
PVector acceleration;    // The Mover's maximum speed
float topspeed;   
Mover() {   
                    // Start in the center   
position = new PVector(width/2,height/2);   
velocity = new PVector(0,0);      
topspeed = 5;    
}      
void update() {            
// Compute a vector that points from position to mouse      
PVector mouse = new PVector(mouseX,mouseY);      
PVector acceleration = PVector.sub(mouse,position);      // Set magnitude of acceleration      
acceleration.setMag(0.2);            // Velocity changes according to acceleration      
velocity.add(acceleration);      // Limit the velocity by topspeed      
velocity.limit(topspeed);      // position changes by velocity      
position.add(velocity);   
 }      
 void display() {      
 stroke(0);      
 strokeWeight(2);      
 fill(127);      
 ellipse(position.x,position.y,48,48);    
 }    
 } 




Mover mover;    
void setup() {    
size(640,360);   
 mover = new Mover();   
 }    
 void draw() {    
 background(255);        // Update the position    
 mover.update();    // Display the Mover    
 mover.display();   
 } 
 

第二章 力

嗯“s”重启
1.小球
生成一组小球，自由落体后进入水面，在出水面，最后模仿进出过程更好的体现在液体中的阻力，主要运用了牛顿定律中的自由落体的公式`

class Mover {
  // position, velocity, and acceleration 
  PVector position;
  PVector velocity;
  PVector acceleration;

  // Mass is tied to size
  float mass;

  Mover(float m, float x, float y) {
    mass = m;
    position = new PVector(x, y);
    velocity = new PVector(0, 0);
    acceleration = new PVector(0, 0);
  }

  void applyForce(PVector force) {
    // Divide by mass 
    PVector f = PVector.div(force, mass);
    // Accumulate all forces in acceleration
    acceleration.add(f);
  }

  void update() {
    // Velocity changes according to acceleration
    velocity.add(acceleration);   
    // position changes by velocity
    position.add(velocity);
    // We must clear acceleration each frame
    acceleration.mult(0);
  }

  // Draw Mover
  void display() {
    stroke(0);
    strokeWeight(2);
    fill(127, 200);
    ellipse(position.x, position.y, mass*16, mass*16);
  }

  // Bounce off bottom of window
  void checkEdges() {
    if (position.y > height) {
      velocity.y *= -0.9;  // A little dampening when hitting the bottom
      position.y = height;
    }
  }
}

2.液体
根据阻力公式，计算小球在液体中所受的阻力。

class Liquid {
  // Liquid is a rectangle
  float x, y, w, h;
  // Coefficient of drag
  float c;

  Liquid(float x_, float y_, float w_, float h_, float c_) {
    x = x_;
    y = y_;
    w = w_;
    h = h_;
    c = c_;
  }

  // Is the Mover in the Liquid?
  boolean contains(Mover m) {
    PVector l = m.position;
    return l.x > x && l.x < x + w && l.y > y && l.y < y + h;
  }

  // Calculate drag force
  PVector drag(Mover m) {
    // Magnitude is coefficient * speed squared
    float speed = m.velocity.mag();
    float dragMagnitude = c * speed * speed;

    // Direction is inverse of velocity
    PVector dragForce = m.velocity.get();
    dragForce.mult(-1);

    // Scale according to magnitude
    // dragForce.setMag(dragMagnitude);
    dragForce.normalize();
    dragForce.mult(dragMagnitude);
    return dragForce;
  }

  void display() {
    noStroke();
    fill(50);
    rect(x, y, w, h);
  }
}

判断小球十分入水

主程序
Mover[] movers = new Mover[9];

Liquid liquid;

void setup() {
size(640, 360);
reset();

liquid = new Liquid(0, height/4, width, height/4, 0.1);
}

void draw() {
background(255);

liquid.display();

PVector dragForce = new PVector(0, 0);

for (int i = 0; i < movers.length; i++) {

if (liquid.contains(movers[i])) {
  
  dragForce = liquid.drag(movers[i]);

  movers[i].applyForce(dragForce);
}


PVector gravity = new PVector(0, 0.1*movers[i].mass);

movers[i].applyForce(gravity);

movers[i].update();
movers[i].display();
movers[i].checkEdges();


stroke(155);

}

fill(0);

if (keyPressed) {
if (key == ‘r’) {
reset();
}
}
}

void mousePressed() {
PVector press = new PVector(0,-6);
for (int i = 0; i < movers.length; i++) {
movers[i].applyForce(press);
}
}

void reset() {
for (int i = 0; i < movers.length; i++) {
movers[i] = new Mover(random(0.5, 3), 40+i*70, 0);
}
}
第三章 振荡
Y=sinx公式，来自直角三角形。在直角三角形中，∠α（不是直角）的对边与斜边的比叫做∠α的正弦，记作sinα，即sinα=∠α的对边/∠α的斜边 。

而本次我使用的就是上方那个正弦公式的延伸公式：

——简谐运动公式。

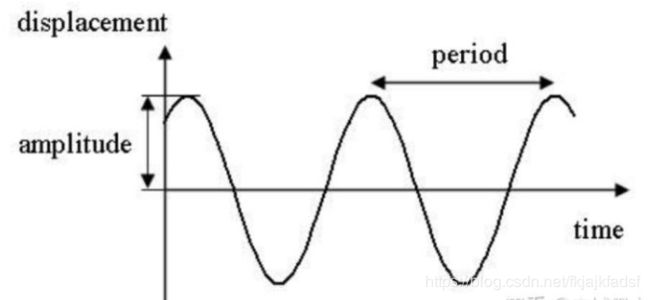
在这个式子中，A为振幅，ω为角速度，t为时间，Φ为初相位。表现起来，这个公式对应的曲线是这样的：

而小球的运动，便是通过简谐运动描述的。

void setup()  
{    
size(400,400);  
}    
void draw()  
{  
  background(255);  
  float period=120;  
  float amplitude = 100;
  float x= amplitude*cos(TWO_PI*frameCount/period);    
  stroke(0);    
  fill(175);    
  translate(width/2,height/2);    
  line(0,0,x,0);    
  ellipse(x,0,40,40); 
 }  

第四章 粒子系统
看了本章内容我决定用以前做的粒子系统加以更改在体现出来，以下为本章的两个重点。
粒子系统的生成
随机点的生成
粒子就是在屏幕中移动的对象，它有位置、速度和加速度变量，有构造函数用于内部变量的初始化，有display()函数用于绘制自身，还有update()函数用于更新位置。
典型的粒子系统中都有一个发射器，发射器是粒子的源头，它控制粒子的初始属性，包括位置、速度等。发射器发射的粒子可能是一股粒子，也可能是连续的粒子流，或是同时包含这两种发射方式。有一点非常关键：在一个典型的粒子系统中，粒子在发 射器中诞生，但并不会永远存在。假设粒子永不消亡，系统中的粒子将越积越多，Sketch的运行速度也会越来越慢，最后程序会挂起。新的粒子不断产生，与此同时，旧的粒子应该不断消亡，只有这样，程序的性能才不会受到影响。决定粒子何时消亡的方法很多，比如，粒子可以和另一个粒子结合在一起，或在离开屏幕时消亡。
用数组实现复杂的粒子系统。

 int num = 1000;//the number of point(s).
float mts = PI/24;//max theta speed.
int r = 100;//radius of the circle
int rdtr = 5;//range of the rdt
int rdu = 1;//radius of circle
//**********
PVector v[]=new PVector[num];
boolean mv = true;
boolean mo = true;
color c[] = new color[num];//color of each point.
float theta[] = new float[num];//original angle of each point.
float mtheta[] = new float[num];//translate angle to math value.
float dtheta[] = new float[num];//speed of theta.
float easing[] = new float[num];
int rdt[] = new int[num];//make a shuffle of radius.
void setup() {
colorMode(RGB,255,255,255);
size(250,250);
for(int i =0;i<num-1;i++){
c[i] = color(random(100,200),random(100,200),random(100,200));
v[i] = new PVector(random(width),random(height));
theta[i] = round(random(360));
dtheta[i] = random(mts);
mtheta[i] = theta[i]/180*PI;
rdt[i] = round(random(-rdtr,rdtr));
easing[i] = random(0.02,0.3);
}
frameRate(60);
}
void draw() {
fill(25,25,25,25);
rect(0,0,width,height);
pushMatrix();
noStroke();
if(mv){
if(mo){
for(int i = 0;i<num-1;i++){
mtheta[i] += dtheta[i];
v[i].lerp(mouseX+cos(mtheta[i])*(rdt[i]+r), mouseY+sin(mtheta[i])*(rdt[i]+r),0,easing[i]);
fill(c[i]);
ellipse(v[i].x, v[i].y, rdu,rdu);
}
}
if(!mo){
for(int i = 0;i<num-1;i++){
v[i].lerp(mouseX+cos(mtheta[i])*(rdt[i]+r), mouseY+sin(mtheta[i])*(rdt[i]+r),0,easing[i]);
fill(c[i]);
ellipse(v[i].x, v[i].y, rdu,rdu);
}
}
}
if(!mv){
if(mo){
for(int i = 0;i<num-1;i++){
mtheta[i] += dtheta[i];
v[i].lerp(mouseX+cos(mtheta[i])*rdt[i], mouseY+sin(mtheta[i])*rdt[i],0,easing[i]);
fill(c[i]);
ellipse(v[i].x, v[i].y, rdu,rdu);
}
}
if(!mo){
for(int i = 0;i<num-1;i++){
v[i].lerp(mouseX+cos(mtheta[i])*rdt[i], mouseY+sin(mtheta[i])*rdt[i],0,easing[i]);
fill(c[i]);
ellipse(v[i].x, v[i].y, rdu,rdu);
}
}
}
popMatrix();
fill(0);
rect(0,0,width,15);
fill(255);
textAlign(LEFT,TOP);

if(mv){
fill(255,0,0);
}
if(!mv){
}
if(mo) {
fill(255,0,0);
}
if(!mo){
fill(255);
}
}
void mousePressed(){
  
mv = !mv;
}
void keyPressed(){
if(key == 's'||key == 'S'){
mo =!mo;
}
}
void mouseWheel(MouseEvent event){
float e = event.getCount();
if(e == -1) r+=10;
if(e == 1) r-=10;
}