最小生成树 加权无向图

最小生成树

加权图：为每条边关联一个权值或成本的图模型

本节我们将学习加权无向图模型并用算法求解最小生成树问题。

最小生成树（MST）：给定一幅加权无向图，找到它的一棵最小生成树。图的生成树是它的一棵含有其所有顶点的无环连通子图。一幅加权无向图的最小生成树是它的一棵权值（树中所有边的权值之和）最小的生成树。

计算最小生成树的两种经典算法：Prim算法 和 Kruskal算法

在计算最小生成树的过程中可能出现各种特殊情况。我们约定如下：只考虑连通图；边的权重可能是0或负数；所有边的权重都各不相同

原理

切分定理

图的一种切分是将图的所有顶点分为两个非空且不重复的两个集合。横切边是一条连接两个属于不同集合的顶点的边。

根据切分定理，我们把加权图中的所有顶点分为两个集合、检查横跨两个集合的所有边并识别哪条边应属于图的最小生成树。

在假设所有的边的权重均不相同的前提下，每幅连通图都只有一棵唯一的最小生成树。切分定理也表明了对于每一种切分，权重最小的横切边必然属于最小生成树。

贪心算法

切分定理是解决最小生成树问题的所有算法的基础。
更准确的说，这些算法都是一种贪心算法的特殊情况：使用切分定理找到最小生成树的一条边，不断重复直到找到最小生成树的所有边。
这些算法相互之间的不同之处在于保存切分和判定权重最小的横切边的方式，但他们都是以下命题的特殊情况：

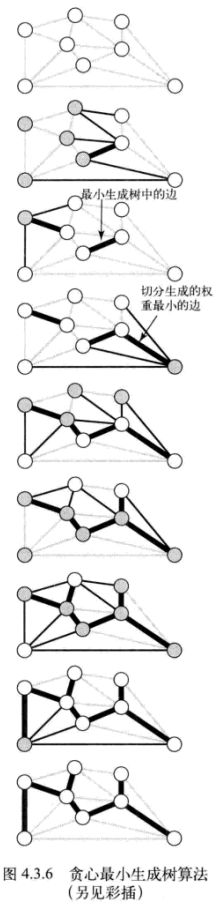
下图展示了这个贪心算法运行的典型轨迹。每一幅图表现的都是一次切分，其中算法识别了一条权重最小的横切边（加粗）并将它加入最小生成树之中。

加权无向图

加权无向图应该如何表示？最简单的方法就是扩展无向图的表示方法：
在邻接矩阵的表示中，可以用边的权重代替布尔值作为矩阵的元素
在邻接表的表示中，可以在链表的结点中增加一个权重域

加权无向边的数据类型

另外一种表示方式，用更加通用的API来处理Edge对象：

该数据结构 提供了either() 和 other(v) 两个方法。
当已知一个顶点v时，用例可以使用 other(v) 来得到边的另一个顶点。
当两个顶点都是未知时，用例可以使用惯用代码 v = e.either()，w = e.other(v) 来访问一个Edge对象e的两个顶点。

Edge类必须实现 Comparable接口 并包含一个 compareTo() 方法。

/*
 * 带权重的边的数据类型
 */
public class Edge implements Comparable<Edge>{
    private final int v;          //顶点之一
    private final int w;          //另一个顶点
    private final double weight;  //权重
    
    public Edge(int v, int w, double weight) {
        this.v = v;
        this.w = w;
        this.weight = weight;
    }
    public double weight() { return weight; }
    
    public int either() { return v; }
    
    public int other(int vertex) {
        if(vertex == v) return w;
        else if(vertex == w) return v;
        else throw new RuntimeException("Inconsisitent edge");
    }

    public int compareTo(Edge that) {
        if(this.weight() < that.weight()) return -1;
        else if(this.weight() > that.weight()) return 1;
        else return 0;
    }
    
    public String toString() { return String.format("%d%-d %.2f", v,w,weight); }
    
}

加权无向图的数据类型

加权无向图的实现很自然地使用了Edge对象，API如下表：
这份API和无向图Graph的API非常相似。两者的两个重要不同之处在于本节API的基础是Edge且添加了一个 edges() 方法。

/*
 * 加权无向图的数据类型
 */
public class EdgeWeightedGraph {
    private final int V;       //顶点总数
    private int E;             //边的总数
    private Bag<Edge>[] adj;   //邻接表
    
    public EdgeWeightedGraph(int V) {
        this.V = V;
        this.E = 0;
        adj = (Bag<Edge>[]) new Bag[V];  //和Queue不同,Bag保证无序
        for(int v=0; v<V; v++) {
            adj[v] = new Bag<Edge>();
        }
    }
    public int V() { return V; }
    public int E() { return E; }
    
    public void addEdge(Edge e) {
        int v = e.either(), w = e.other(v);  //
        adj[v].add(e);
        adj[w].add(e);
        E++;
    }
    
    public Iterable<Edge> adj(int v) {
        return adj[v];
    }
    
    //返回加权无向图中的所有边
    public Iterable<Edge> edges() {
        Bag<Edge> b = new Bag<Edge>();
        for (int v = 0; v < V; v++) {
            for (Edge e : adj(v)) {
                if (e.other(v) > v)
                    b.add(e);
            }
        }
        return b;
    }
}

最小生成树的API

在API中会定义一个接受加权无向图为参数的构造函数，并且支持能够为用例返回图的最小生成树和其权重的方法。