2019 力扣杯全国秋季编程大赛

1. 猜数字

题目描述

小A 和 小B 在玩猜数字。小B 每次从 1, 2, 3 中随机选择一个，小A 每次也从 1, 2, 3 中选择一个猜。他们一共进行三次这个游戏，请返回 小A 猜对了几次？
输入的guess数组为 小A 每次的猜测，answer数组为 小B 每次的选择。guess和answer的长度都等于3。
示例 1：
输入：guess = [1,2,3], answer = [1,2,3]
输出：3
解释：小A 每次都猜对了。

示例 2：
输入：guess = [2,2,3], answer = [3,2,1]
输出：1
解释：小A 只猜对了第二次。

题解

水题，不多解释。

代码

class Solution {
public:
    int game(vector<int>& guess, vector<int>& answer) {
        int res = 0;
        for(int i = 0; i < 3; ++i){
            res = res + (guess[i] == answer[i]);
        }
        return res;
    }
};

2. 分式化简

题目描述

有一个同学在学习分式。他需要将一个连分数化成最简分数，你能帮助他吗？
连分数是形如上图的分式。在本题中，所有系数都是大于等于0的整数。
输入的cont代表连分数的系数（cont[0]代表上图的a0，以此类推）。返回一个长度为2的数组[n, m]，使得连分数的值等于n / m，且n, m最大公约数为1。

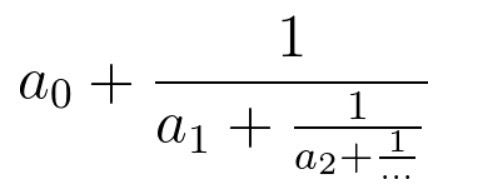
示例 1：
输入：cont = [3, 2, 0, 2]
输出：[13, 4]
解释：原连分数等价于3 + (1 / (2 + (1 / (0 + 1 / 2))))。注意[26, 8], [-13, -4]都不是正确答案。

示例 2：
输入：cont = [0, 0, 3]
输出：[3, 1]
解释：如果答案是整数，令分母为1即可。

限制：
cont[i] >= 0
1 <= cont的长度 <= 10
cont最后一个元素不等于0
答案的n, m的取值都能被32位int整型存下（即不超过2 ^ 31 - 1）。

题解

这个题规律很明。从最内侧来看，形式都是形如$a+\frac{1}{b}$，当只有一个数时，直接返回cont[0]。当数大于1时，第一次计算的a = cont[len - 2]， b = cont[len - 1]，计算出的结果作为新的b，然后a = cont[len - 3]……

代码

class Solution {
public:
    int gcd(int num1, int num2){//求两个数的最大公约数
        return num2 == 0?num1:gcd(num2, num1 % num2);
    }
    vector<int> cal(vector<int>num1, vector<int>num2){//计算num1 + 1 / num2，注意num1与num2都是分数的形式
        vector<int>res(2);
        res[0] = num1[0] * num2[0] + num1[1] * num2[1];
        res[1] = num1[1] * num2[0];
        int tmp = gcd(res[0], res[1]);//分数化成最简分数，同时除以分子分母的最大公约数
        res[0] = res[0] / tmp;
        res[1] = res[1] / tmp;
        return res;
    }
    vector<int> fraction(vector<int>& cont) {
        int len = cont.size();
        vector<int>res({cont[len - 1], 1});
        if(len == 1){//长度为1时，直接返回仅有的一个元素
            return vector<int>({cont[0], 1});
        }
        for(int i = len - 1; i >= 1; --i){//循环计算
            res = cal(vector<int>({cont[i - 1],1}), res);
        }
        return res;
    }
};

大神代码（JOHNKRAM）

代码更加精简，思路相同

class Solution {
public:
    long long gcd(long long x,long long y)
    {
        return y?gcd(y,x%y):x;
    }
    vector<int> fraction(vector<int>& cont) {
        long long x,y,n=cont.size(),i;
        x=cont[n-1];//分子
        y=1;//分母
        for(i=n-2;~i;i--)
        {
            swap(x,y);//颠倒分子与分母
            x+=cont[i]*y;
        }
        i=gcd(x,y);//简化分子与分母
        x/=i;
        y/=i;
        vector<int> ans;
        ans.push_back(x);
        ans.push_back(y);
        return ans;
    }
};

3. 机器人大冒险

题目描述

力扣团队买了一个可编程机器人，机器人初始位置在原点(0, 0)。小伙伴事先给机器人输入一串指令command，机器人就会无限循环这条指令的步骤进行移动。指令有两种：
U: 向y轴正方向移动一格
R: 向x轴正方向移动一格。
不幸的是，在 xy 平面上还有一些障碍物，他们的坐标用obstacles表示。机器人一旦碰到障碍物就会被损毁。
给定终点坐标(x, y)，返回机器人能否完好地到达终点。如果能，返回true；否则返回false。
示例 1：
输入：command = “URR”, obstacles = [], x = 3, y = 2
输出：true
解释：U(0, 1) -> R(1, 1) -> R(2, 1) -> U(2, 2) -> R(3, 2)。

示例 2：
输入：command = “URR”, obstacles = [[2, 2]], x = 3, y = 2
输出：false
解释：机器人在到达终点前会碰到(2, 2)的障碍物。

示例 3：
输入：command = “URR”, obstacles = [[4, 2]], x = 3, y = 2
输出：true
解释：到达终点后，再碰到障碍物也不影响返回结果。

限制：
2 <= command的长度 <= 1000
command由U，R构成，且至少有一个U，至少有一个R
0 <= x <= 1e9, 0 <= y <= 1e9
0 <= obstacles的长度 <= 1000
obstacles[i]不为原点或者终点

题解

考试的时候初次尝试：看到题目中给了起点和终点，还有一个指令串，萌生的第一个想法就是直接按照指令模拟，结果代码连给的第一个示例都过不了。开始怀疑自己审题是否出现错误，重读题目发现指令可以无限循环执行，发现初始的方法似乎行不通。
AC的方法：先判断按照机器人在无障碍的情况下，是否能到达终点，不能的话，直接返回false。能的话，再看机器人在向终点移动的过程中是否能碰到障碍物。实际上仍是判断机器人能否在无障碍的情况下，到达障碍物的位置且障碍物必须要在原点与终点之间。
判断能否可达时，有一个小优化，先走n次完整的comand指令，将机器人移动到终点附近，再走部分串，这样的效率会高很多。

代码

class Solution {
public:
    int step_u, step_r;
    bool canReach(string command, int x, int y){//判断能否可达
        int step = min(y / step_u,  x / step_r);//先执行完整的command
        int now_x = step * step_r;
        int now_y = step * step_u;
        if(x - now_x + y - now_y >= command.size()){//不可达
            return false;
        }
        if(x- now_x + y - now_y == 0){//可达
            return true;
        }
        else{
            for(int i = 0; i < command.size(); ++i){//再执行部分的command
                if(command[i] == 'U'){
                    ++now_y;
                    if(now_y == y && now_x == x){
                        return true;
                    }
                }
                else{
                    ++now_x;
                    if(now_y == y && now_x == x){//可达
                        return true;
                    }
                }
            }
            return false;
        }
    }
    bool robot(string command, vector<vector<int>>& obstacles, int x, int y) { 
        step_u = 0, step_r = 0;
        for(int i = 0; i < command.size(); ++i){//统计command中up与right的次数，用于reach时的优化。
            if(command[i] == 'U'){
                ++step_u;
            }
            else{
                ++step_r;
            }
        }
        if(canReach(command, x, y)){//无障碍物下可达终点
            for(int i = 0; i < obstacles.size(); ++i){//判断能否到达障碍物
                if((obstacles[i][0] <= x && obstacles[i][1] < y) ||(obstacles[i][0] < x && obstacles[i][1] <= y)){
                    if(canReach(command, obstacles[i][0], obstacles[i][1]))//碰到障碍物
                        return false;
                }
            }
            return true;
        }
        else{//无障碍物下不可达终点
            return false;
        }
    }
};

大神代码（JOHNKRAM）

我真想把膝盖献给第一名，思路太清晰了，第二个for循环太惊艳了，直接看代码吧。

class Solution {
public:
    bool robot(string command, vector<vector<int>>& obstacles, int x, int y) {
        int a=0,b=0,u=0,v=0;
        for(auto i:command)if(i=='R')a++;//统计指令中up与right的次数
        else b++;
        bool c=0;
        for(auto i:command)//逐步执行指令（这里太妙了）
        {
            for(auto j:obstacles)if(j[0]<=x&&j[1]<=y&&(j[0]-u)%a==0&&(j[1]-v)%b==0&&(j[0]-u)/a==(j[1]-v)/b)return 0;//若执行部分指令，可到达原点与终点间的某个障碍物，则直接返回false
            if((x-u)%a==0&&(y-v)%b==0&&(x-u)/a==(y-v)/b)c=1;//可以到达终点，更新标记
            if(i=='R')u++;//统计已执行的指令中的up与right的次数
            else v++;
        }
        return c;
    }
};

4. 覆盖

你有一块棋盘，棋盘上有一些格子已经坏掉了。你还有无穷块大小为1 * 2的多米诺骨牌，你想把这些骨牌不重叠地覆盖在完好的格子上，请找出你最多能在棋盘上放多少块骨牌？这些骨牌可以横着或者竖着放。
输入：n, m代表棋盘的大小；broken是一个b * 2的二维数组，其中每个元素代表棋盘上每一个坏掉的格子的位置。
输出：一个整数，代表最多能在棋盘上放的骨牌数。
示例 1：
输入：n = 2, m = 3, broken = [[1, 0], [1, 1]]

输出：2
解释：我们最多可以放两块骨牌：[[0, 0], [0, 1]]以及[[0, 2], [1, 2]]。（见下图）

示例 2：
输入：n = 3, m = 3, broken = []
输出：4
解释：下图是其中一种可行的摆放方式

限制：
1 <= n <= 8
1 <= m <= 8
0 <= b <= n * m

题解

比赛的时候4、5题没做出来，第4题用的dfs，一直显示超时，感觉dfs应该能做，只是优化没做到位。这里只能从大神们的代码中窥出他们的思路。

欢迎加入LeetCode周赛讨论群！