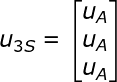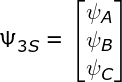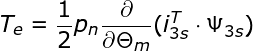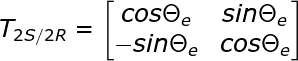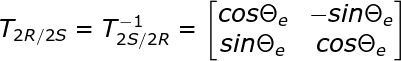PMSM 控制技术探究与仿真1：三相PMSM的数学建模与坐标变换

  永磁同步电机（PMSM：permanent magnet synchronous motor）是一个强耦合、复杂的非线性系统，为了能够更好地理解PMSM及其控制算法，特此开启这个PMSM的博客系列。本系列基于《线代永磁同步电机控制原理及MATLAB仿真》（袁雷，北京航空航天大学出版社）以及鄙人看过的论文等资料进行编撰。下面的链接里可以下载该书的PDF、例程模型和TI电机驱动PPT。将资料吃透有益于理解PMSM的矢量控制方法。转载本博客请注明出处。

  https://download.csdn.net/download/huagengpai1994/10811757

---

1，三相PMSM的基本数学模型

  1.1 三相PMSM 的结构

  当三相PMSM转子磁路的结构不同时，电机的运行性能、控制方法、制造工艺和适用场合也会不同。目前，根据永磁体转子上的位置不同，三相PMSM的转子结构可以分为表贴式和内置式两种结构，具体如下图所示：

  对于表贴式转子结构而言，由于其具有结构简单、制造成本低和转动惯量小等优点，在恒功率运行范围不宽的三相PMSM 和永磁无刷直流电机中得到广泛应用。表贴式转子结构中的永磁磁极易于实现最优设计，能使电机的气隙磁密波形趋于正弦波分布，进而提高电机的运行性能。内置式转子结构可以充分利用转子磁路不对称所产生的磁阻转矩，提高电机的功率密度，使得电机的动态性能较表贴式转子结构有所玫善，制造工艺也较简单，但漏磁系数和制造成本都较表贴式转子结构大。对于采用稀土永磁材料的电机来说，由于永磁材料的磁导率接近1，所以表贴式转子结构在电滋性能上属于隐极转子结构；而内置式转子结构相邻永磁磁极间有着磁导率很大的改磁材料，在电磁性能上属于凸极转子结构。

  1.2 基本数学模型

  对于三相PMSM而言，基本的可变输入是三相交流电流，即电流矢量（包括大小和角度），输出是转矩和转速。在三相PMSM里面三相电流的电角度严格互差120度，所以只能变动电流的大小。构建数学模型的意义在于，搞明白在被控对象的每一状态下，输入怎样的电流（或电压）会输出怎样的转矩和转速。研究清楚这个后，相当于知道了对于被控对象，在当下瞬态给一个作用后在下一个瞬态会变化成什么样。然后，欲使对象从此状态到达彼状态，就需要设计控制方法，以此来确定在每时每刻该作用什么。总结一下就是，先构建数学模型（包括力学模型、动力学模型等），再设计控制器。
  为了简化分析，假设三相PMSM为理想电机，且满足下列条件：

  - 忽略电机铁芯的饱和
  - 不计电机中的涡流和磁滞损耗
  - 电机中的电流为对称的三相正弦波电流

  这样，自然坐标系下PMSM的三相电压方程可以写为：
  

  u_3S、R和i_3S分别为：三相绕组的相电压、相电阻和相电流。Ψ_3S为三相绕组的磁链变化率，磁链的方程为：
  

  L_3S为三相绕组的电感；ψ_fF_3S(θ_e)整体表示永磁体在三相绕组中产生的磁链，ψ_f为永磁体磁链，F_3S(θ_e)为与电角度相关的系数(在书中该处的说法是有问题的)。
  磁链是导电线圈或电流回路所链环的磁通量。其大小为导电线圈匝数N与穿过该线圈各匝的平均磁通量φ的乘积。电机都是遵循法拉第电磁感应定律，按照电能—磁能—机械能的方法驱动。
  以下为矩阵的具体表示：
  

        

  其中，L_m3为定子互感；L_m3为定子漏感，Θ_e表示电角度。解释一下电角度：

  上图中，u,v,w为三相绕组，2极的意思是极对数为2，也就是说有2极×3相=6块小扇区。可以看到N从V到达下一个V对于三相电流而言走完了一个完整的周期又回到了初始状态，但是电机并没有转完一整圈。换言之，如果电机完整转完一圈，那么对于三相电流而言不过是重复了极对数遍周期过程。所以控制上直接讨论的是电角度，然后换算到机械角度。多机电机的显而易见的：转矩和转速的控制更精确、转动更平滑。缺点是多极电机的电动势中高次谐波增加，齿槽转矩增加，由高次谐波引起的损耗增加。

电角度=机械角度×极对数

  解释结束，继续推导公式。
  根据机电能量转换原理，电磁转矩T_e等于磁场储能与机械角Θ_m位移的偏导，因此有：

  其中，p_n为三相PMSM的极对数。
  另外，由牛顿第二定理可得电机的机械运动方程为

  可以看出电磁转矩的方程比较复杂，为了能达到想要的转矩，去确定三相电流值是很困难的。总而言之，如此建立的三相PMSM的数学模型是一个比较复杂且强耦合的多变量系统。必须要对模型进行解耦，降阶（转矩方程中有矩阵乘法——自变量与自变量的乘积，会导致多阶）。

---

2，三相PMSM的坐标变换

  2.1 d-q轴数学模型是什么

  下述英文来自TI的官方PPT，该PPT在开头链接里有。动画是我从PPT里面扒出来做的。
  Assume we have a two or three phase AC motor as shown in the bottom-left animation. By properly controlling the motor’s sinusoidal currents in real time, you can create a smoothly rotating magnetic flux pattern as shown, where the frequency of rotation corresponds to the frequency of the current sinewaves. If you then place a magnetized rotor inside the stator frame, the magnetic attraction between the rotating stator flux and the rotor magnets will cause the rotor to follow this rotation. However, the animation indicates a condition of relatively low motor loading, as indicated by the fact that the orientation of the rotor magnets and stator flux are the same. As you load down the motor, you will see that the rotor angle will start to lag the stator flux angle. This effect is plotted in the center diagram, where generated motor torque is plotted against this lag angle. When the rotor flux axis is lagging the stator flux angle by 90 degrees, this is the condition of maximum torque for a given amount of stator coil current. So depending on whether we would like clockwise or counterclockwise torque, we would like the relative angle to be either -90 or +90 degrees.（假设我们有一个两相或三相交流电动机，如左下角动画所示。通过适当地实时控制电机的正弦电流，可以创建如图所示的平滑旋转的磁通模式，其中旋转的频率对应于电流正弦波的频率。如果你在定子框架内放置一个磁化的转子，那么在旋转的定子磁通和转子磁铁之间的磁吸引力将导致转子跟随这个旋转。但是，该动画显示电机负载相对较低的情况，如转子磁铁和定子磁通的方向相同的事实所示。当你把马达装下去的时候，你会发现转子的角度会开始滞后于定子磁通角度。这种效应在中心图中绘制，其中产生的电机转矩相对于这个滞后角绘制。当转子磁链轴滞后于定子磁链角90度时，这是给定定子线圈电流时最大转矩的条件。因此，根据我们是顺时针还是逆时针扭矩，我们希望相对角度是-90度或+90度。）

  It turns out that we can’t instantaneously control the axis of the rotor magnets to be at +/- 90 degrees with respect to the angle of the stator flux. But we CAN instantaneously control the angle of the stator flux to be at +/- 90 degrees with respect to the axis of the rotor magnets. This axis is called the “d” or “direct” axis. All we need is some kind of measurement to tell us where the d-axis is at, (and consequently, what angle the rotor flux is at), and from this information, we control the currents into the motor to produce a stator flux vector which is 90 degrees with respect to it. This 90 degree axis is called the “q” or “quadrature” axis. As the motor is spinning, the d-axis is also spinning. So we need to constantly update the stator currents accordingly so as to reposition the stator flux pattern to always be offset by 90 degrees from the d-axis. This is shown in real time by the animation on the right, where the red vector represents the rotor flux on the d-axis, and the green vector represents the stator flux on the q-axis. If you want more torque, you simply increase the stator flux intensity by increasing the instantaneous stator current levels, which in effect makes the green vector longer. But you always want to keep that vector to be at 90 degrees with respect to the rotor flux vector. （结果表明，我们不能瞬时控制转子磁铁的轴线相对于定子磁通角为+/-90度。但我们可以瞬间控制定子磁通相对于转子磁铁轴线的角度为+/-90度。这个轴称为“D”轴或“直”轴。我们只需要某种测量来告诉我们d轴在什么位置（以及转子磁通在什么角度），并且根据这个信息，我们控制进入电机的电流，以产生一个相对于它90度的定子磁通矢量。这个90度轴称为“q”或“正交”轴。当电机旋转时，D轴也在旋转。因此，我们需要不断地更新定子电流，以便重新定位定子磁通模式，使其总是偏离d轴90度。这在右边的动画中实时显示，其中红色矢量表示d轴上的转子磁通，绿色矢量表示q轴上的定子磁通。如果你想要更多的转矩，你只要通过增加瞬时定子电流水平来增加定子磁链强度，这实际上使绿色矢量变长。但是你总是想保持这个向量相对于转子磁通向量在90度。）

  简单来说就是：通过控制三相电流可以让定子绕组产生旋转的磁场，该旋转磁场致使固定了永磁体的转子产生相对转动。且转子磁铁的轴线相对定子磁通的角度为90度（正负不同会使转矩方向不同）时，磁场产生的转动效果最好（简单理解为正交时转矩最大）。那么我们就可以监测转子磁铁的轴线角度并且实时改变定子磁通的角度和大小，以达到控制转子的目的。称转子磁铁的轴线方向为“d”轴或“直轴”（红色），实时控制改变的定子磁通矢量为“q”轴或“交轴”（绿色）。d-q 正交轴是与电机转子随动的，矢量控制或者叫场定向控制（Field Oriented Control)就是这么来的。值得注意的一个细节是，d-q轴是在电角度意义上说的。也就是说对于多极电机，转子完全旋转一圈，d-q轴会旋转多圈，并不只是图示的这一种情况。
  从这个思路出发构造出来的数学模型叫d-q轴两相旋转坐标模型，简称d-q模型。
  电压方程为：

  定子磁链方程为：

  两方程组合后电压方程重写为：

  其中：u_d、u_q分别是定子电压的d-q轴分量；i_d、i_q分别是定子电流的d-q轴分量；R是定子电阻；ψ_d、ψ_q为定子磁链的d-q轴分量；ω_e是电角速度；L_d、L_q分别是d-q轴电感分量；ψ_f代表永磁体磁链。
  电磁转矩方程可以写为：

  上面的四组方程是针对内置式三相PMSM建立的数学模型；对于标贴式三相PMSM，定子电感满足L_d=L_q=L_s。因此表贴式三相PMSM的数学模型相对简单一些。
  另外，还会经常用到这几个重要的关系式：

  其中：ω_m为电机的机械角速度，rad/s。N_r为电机的转速，r/min。
  现在来看整个数学模型“顺”了很多，后面矢量控制中若用i_d=0的方式，那么转矩就只和i_q相关，电压方程也简化了很多。定子电压方程有两个，等于自变量的个数且自变量不相关，整体上这个d-q模型实现了完全的解耦。这样欲使达到某一个转矩（转速与转矩相关，位置与转速相关，所以内环是控转矩），就知道需要怎样的i_q和i_d。但是为得到想要的i_q和i_d又该怎么样去输入三相电流呢，还有d-q轴的电感如何去合成呢，这就需要坐标变换来完成了。

  2.2坐标变换——克拉克变换与帕克变换

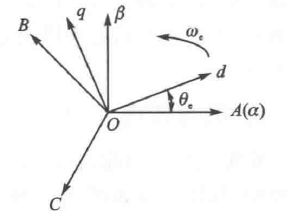
  在电角度的平面里面，A,B,C代表三相交流电的矢量。因为规定了三相交流电互差120度所以A,B,C的方向是固定的，只有大小可以变化。α与β是固定的正交轴（相当于规范的x,y轴，我也不知道为啥这里要用αβ），其中α与A方向重合。d-q轴就是前文中说到的随电机旋转的直轴与交轴。

  我们的目的是通过改变A,B,C三个矢量的大小，然后映射到d-q轴上形成想要的d-q轴矢量。但是d-q轴是随时在变化的，而且直接转换，计算起来不太容易，所以我们分两步进行。
   第一步：将A,B,C映射到标准正交轴α与β上 ———— 克拉克变换。
  第二步：将α与β轴上的矢量映射到d-q轴 ——— 帕克变换。
  （说实在的，凭这俩3×3的简单矩阵就可以在无数工程人心中留下大名，克拉克和帕克真是赚到了。“一个人的命运，当然要靠自我奋斗，但也要考虑到历史的进程。”）

   克拉克变换如下：

  其中：f代表电压、电流或磁链等变量；T_3s/2s为坐标变换矩阵，表示为

  MATLAB的simulink里面是这个样子的：

  变换矩阵前的系数为2/3,是根据幅值不变作为约束条件得到的，即依据相电压峰值；当采用功率不变作为约束条件时，该系数变为根号下的2/3，即依据相电压有效值（原谅我在html中不会打根号，知道的大神评论一下）。
  反过来就是反克拉克变换了，也就是矩阵求逆。

  同样的可以得到帕克变换的公式如下：

  将两个变换合起来就得到了从三相到d-q轴的变换方法，其系数矩阵如下。

  反变换的系数矩阵如下：

  至此，PMSM控制技术的第一篇就结束了。鄙人制作真的很辛苦啊，毕竟第一篇，要开个好头。要是有路过的大神，请指出不足之处啊。