泰坦尼克号生存预测(一)-- 数据处理
项目及数据集来自Kaggle。
持续更新中......
1. 提出问题
建立模型预测乘客是否生还。
2. 理解数据
数据特征含义:survival为目标变量,其他为特征。
| Variable | Definition | Key |
|---|---|---|
| survival | Survival | 0 = No, 1 = Yes |
| pclass | Ticket class | 1 = 1st, 2 = 2nd, 3 = 3rd |
| sex | Sex | |
| Age | Age in years | |
| sibsp | # of siblings / spouses aboard the Titanic | |
| parch | # of parents / children aboard the Titanic | |
| ticket | Ticket number | |
| fare | Passenger fare | |
| cabin | Cabin number | |
| embarked | Port of Embarkation | C = Cherbourg, Q = Queenstown, S = Southampton |
# load libraries of anlysis and visualization
import numpy as np
import pandas as pd
import re # Regular Expression operations
import matplotlib.pyplot as plt
%matplotlib inline
train = pd.read_csv('train.csv')
test = pd.read_csv('test.csv')
# 观察数据
train.head() #前5行数据
train.sample(5) #随机5行数据
train.describe() #各列统计数据
train.dtypes #数据类型# 载入seaborn作图
import seaborn as sns
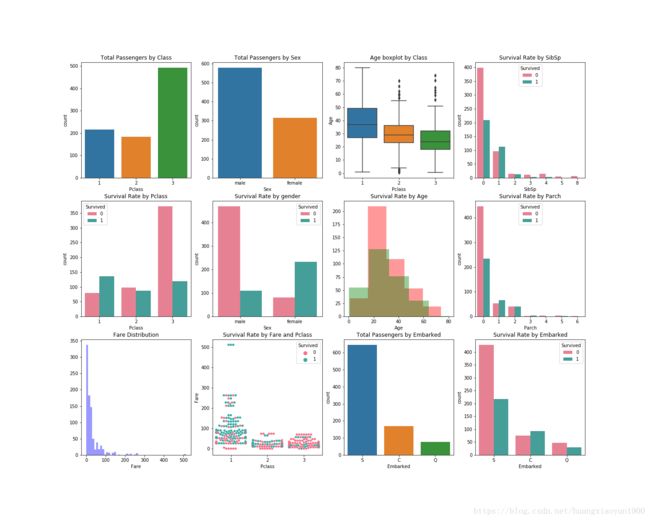
f,ax = plt.subplots(3,4,figsize=(20,16))
sns.countplot('Pclass',data=train,ax=ax[0,0])
sns.countplot('Sex',data=train,ax=ax[0,1])
sns.boxplot(x='Pclass',y='Age',data=train,ax=ax[0,2])
sns.distplot(train['Fare'].dropna(),ax=ax[2,0],kde=False,color='b')
sns.countplot('Embarked',data=train,ax=ax[2,2])
sns.countplot('SibSp',hue='Survived',data=train,ax=ax[0,3],palette='husl')
sns.countplot('Parch',hue='Survived',data=train,ax=ax[1,3],palette='husl')
sns.countplot('Embarked',hue='Survived',data=train,ax=ax[2,3],palette='husl')
sns.countplot('Pclass',hue='Survived',data=train,ax=ax[1,0],palette='husl')
sns.countplot('Sex',hue='Survived',data=train,ax=ax[1,1],palette='husl')
sns.distplot(train[train['Survived']==0]['Age'].dropna(),ax=ax[1,2],kde=False,color='r',bins=5)
sns.distplot(train[train['Survived']==1]['Age'].dropna(),ax=ax[1,2],kde=False,color='g',bins=5)
sns.swarmplot(x='Pclass',y='Fare',hue='Survived',data=train,ax=ax[2,1],palette='husl')
ax[0,0].set_title('Total Passengers by Class')
ax[0,1].set_title('Total Passengers by Sex')
ax[0,2].set_title('Age boxplot by Class')
ax[0,3].set_title('Survival Rate by SibSp')
ax[1,0].set_title('Survival Rate by Pclass')
ax[1,1].set_title('Survival Rate by gender')
ax[1,2].set_title('Survival Rate by Age')
ax[1,3].set_title('Survival Rate by Parch')
ax[2,0].set_title('Fare Distribution')
ax[2,1].set_title('Survival Rate by Fare and Pclass')
ax[2,2].set_title('Total Passengers by Embarked')
ax[2,3].set_title('Survival Rate by Embarked')
3. 数据清理
a. 找出异常值和离群点
# 检测异常值 因为此数据中没有明显异常点,故检测离群点(1.5个IQR(四分位距)以外的点)
'''
定义离群点函数
输入:dataset,MAX离群特征个数n,特征名
输出:超过n个离群特征的样本index
'''
# 调取collections的Counter,用于对list计数
from collections import Counter
def detect_outliers(df,n,feature):
outlier_indices = []
for f in feature:
# 1st quartile(25%)
Q1=np.percentile(df[f],25)
# 3rd quartile(75%)
Q3=np.percentile(df[f],75)
# Interquartile range四分位距
IQR=Q3-Q1
outlier_step=1.5*IQR
# 生成该特征中为离群点的样本index
outlier_list_col = df[(df[f]<(Q1-outlier_step))|(df[f]>(Q3+outlier_step))].index
# 生成一个含有离群点样本index的list
outlier_indices.extend(outlier_list_col)
# 对该list计数,生成字典key为要计数的值,value为key的计数值
outlier_indices = Counter(outlier_indices)
multiple_outliers = list(k for k,v in outlier_indices.items() if v>n)
return multiple_outliers
# 找出同时有两个以上特征为离群点的样本
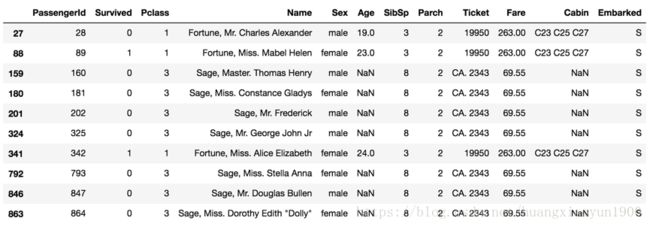
Outliers_to_drop=detect_outliers(train,2,['Fare','Age','SibSp','Parch'])
train.loc[Outliers_to_drop]由上述结果可以: 1. 存在10个以上超过2个特征为离群点的样本; 2. 有三位乘客费付了较高的票价263;3. 有7位乘客有较多的兄弟姐妹或伴侣在此船上;4. 结合之前train.describe()结果,这些离群点并不是偏得离谱,因此,应该保留下来。
b. 缺失值处理
# 统计各列缺失值个数
train.isnull().sum()
test.isnull().sum()在train和test两个数据集中,"Age", "Cabin"中含有较多缺失值,在train数据集中embarked含有两个缺失值,在test数据集中Fare有一个缺失值。
4. 特征工程-二变量统计分析
对特征分析第一步就要看特征是numerical/ordinal values,一般分两种情况:
1) 定性型Qualitative data: discrete离散型
名义型数据如姓名,或分类型数据如性别等
2) Numeric/Qualitative data连续型或可排序的数据:
数值离散型数据:如Pcalss等级这类可以排序的数据,或连续型数据
a. 上船地点
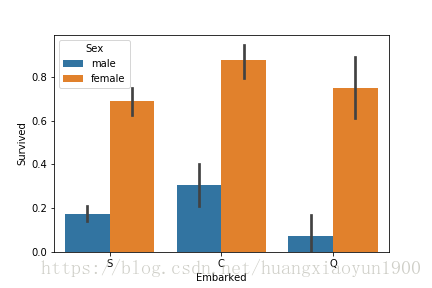
# Embarked
sns.barplot(x = 'Embarked',y='Survived',hue='Sex',data=train)单从此图看,女性的存活率明显高于男性,从哪里上船与存活率没有明显的关系,需要进一步探索。
b. 姓名
姓名长度
train['Name_length']=train['Name'].apply(len)
sum_name = train[['Name_length','Survived']].groupby(['Name_length'],as_index=False).sum()
average_name = train[['Name_length','Survived']].groupby(['Name_length'],as_index=False).mean()
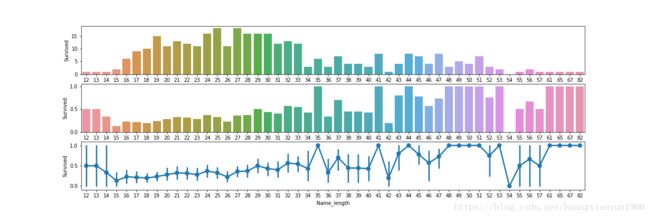
f,(axis1,axis2,axis3) = plt.subplots(3,1,figsize=(18,6))
sns.barplot(x = 'Name_length',y='Survived',data=sum_name,ax=axis1)
sns.barplot(x='Name_length',y='Survived',data=average_name,ax=axis2)
sns.pointplot(x='Name_length',y='Survived',data=train,ax=axis3)c. 性别
将性别转换为数值型二分类数据
full_data = [train,test]
Survival = train['Survived']
# 将性别数值化
for dataset in full_data:
dataset['Sex']=dataset['Sex'].map({'female':0,'male':1}).astype(int)d. 年龄
# Age
# 不同年龄存活率分布
# sns.FacetGrid可以绘制多个轴变量相同的图,aspect设置图aspect ratio纵横比,size设置图片高度,通常需要用.map()作图。
a=sns.FacetGrid(train,hue='Survived',aspect=6)
a.map(sns.kdeplot,'Age',shade=True)
a.set(xlim=[0,train['Age'].max()])
a.add_legend()由以上核密度图可知:存活的人中,小孩和30左右的人占比较高,而未存活的人集中在23左右,且右偏。
将年龄离散化:
# 由于年龄有较多缺失值,用均值正负一个标准差内的值对其填充
for dataset in full_data:
age_avg = dataset['Age'].mean()
age_std = dataset['Age'].std()
age_null_count = dataset['Age'].isnull().sum()
# 对缺失值填充
age_null_random_list = np.random.randint(age_avg-age_std,age_avg+age_std,size=age_null_count)
dataset['Age'][np.isnan(dataset['Age'])]=age_null_random_list
dataset['Age']=dataset['Age'].astype(int)
# 对年龄离散化
# 若使用pd.qcut()可自动离散化,dataset['Age]=pd.qcout(dataset['Age'],6,labels=False)
# 本例自定义
dataset.loc[dataset['Age']<=14,'Age_level'] = 1
dataset.loc[(dataset['Age']>14)&(dataset['Age']<=30),'Age_level'] = 2
dataset.loc[(dataset['Age']>30)&(dataset['Age']<=40),'Age_level'] = 3
dataset.loc[(dataset['Age']>40)&(dataset['Age']<=50),'Age_level'] = 4
dataset.loc[(dataset['Age']>50)&(dataset['Age']<=60),'Age_level'] = 5
dataset.loc[(dataset['Age']>60),'Age_level'] = 6
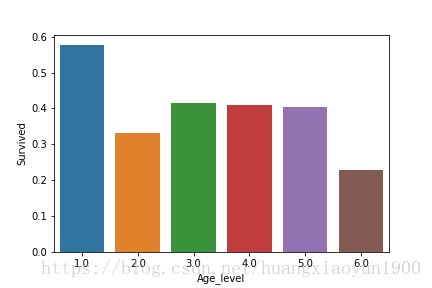
train['Age_level'].value_counts()
Age_Surv=train[['Age_level','Survived']].groupby('Age_level',as_index=False).mean().sort_values(by='Age_level',ascending=False)
sns.barplot(x='Age_level',y='Survived',data=Age_Surv)由上图可知:年龄在14岁以下的儿童存活率明显高于其他年龄段的人,年龄在60岁以上的老年人存活率明显低于其他年龄段的人。
e. 家庭:SibSp/Parch
# 用 familysize 来表示SibSp和Parch
for dataset in full_data:
dataset['Familysize']=dataset['SibSp']+dataset['Parch']+1
# 用isAlone列表示是否独自一人上船
dataset['isAlone']=0
dataset.loc[dataset['Familysize']==1,'isAlone']=1
# 用boy列表示是否为男孩
dataset['boy']=0
dataset.loc[(dataset['Sex']==1)&(dataset['Age_level']==0),'boy']=1
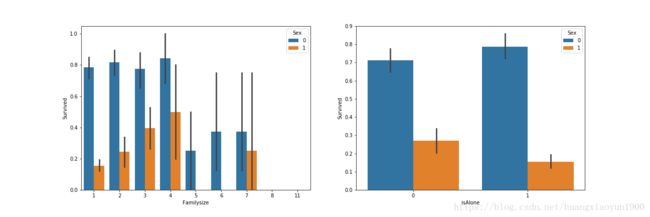
f, (axis1,axis2) = plt.subplots(1,2, figsize=(18,6))
sns.barplot(x='Familysize',y='Survived',hue='Sex',data=train,ax=axis1)
sns.barplot(x='isAlone',y='Survived',hue='Sex',data=train,ax=axis2)由上图可知,是否有家人陪同isAlone存活率没有明显的差别,反而是男女的存活率有明显的差别。
f. 费用
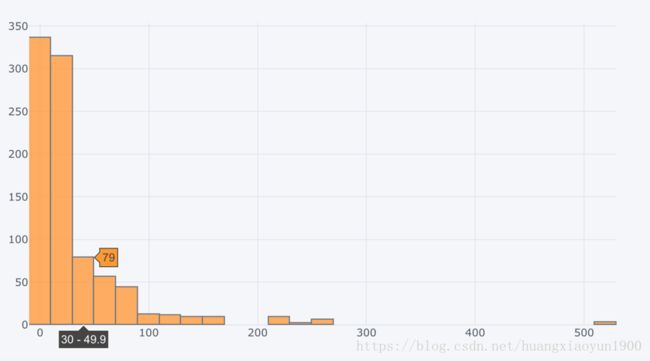
# 使用cufflinks画交互图
import cufflinks as cf
cf.go_offline()
train['Fare'].iplot(kind=hist,bins=30)交互式图表的优点是鼠标指哪里就显示哪里的数值。
# 处理【'Fare'】缺失值,用中位数填充
for dataset in full_data:
dataset['Fare'].fillna(dataset['Fare'].median)
# 看看费用分布图
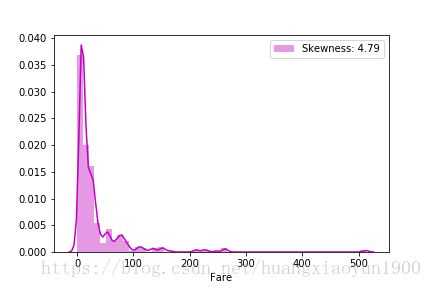
sns.distplot(train['Fare'],color = 'm',label='Skewness: %.2f'%(train['Fare'].skew()))
plt.legend(loc='best')由以上费用分布图可以看出,费用分布严重右偏,这会造成统计量右偏,因此,可以将数据对数化来降低偏度。
# 取对数,np.log()
for dataset in full_data:
dataset['Fare_log']=dataset['Fare'].map(lambda i: np.log(i) if i > 0 else 0)
f, ax = plt.subplots(figsize=(20,6))
sns.distplot(train['Fare_log'][train['Survived']==0],color='r',label='Skewness: %.2f'%(train['Fare_log'].skew()))
sns.distplot(train['Fare_log'][train['Survived']==1],color='b',label='Skewness: %.2f'%(train['Fare_log'].skew()))
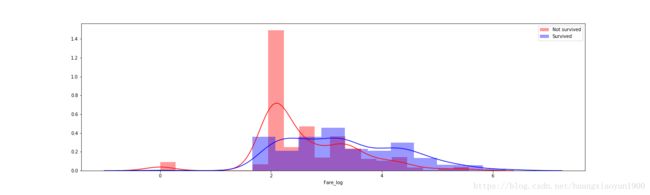
plt.legend(['Not survived','Survived'])由上图可以看出,log['Fare'] 高于2.7的有更高的存活率,而低于2.7的存活率较低。
将数值离散化:
# 将log('Fare')离散化分析
for dataset in full_data:
dataset.loc[dataset['Fare_log']< 2.7,'Fare_log'] = 1
dataset.loc[(dataset['Fare_log']>= 2.7)&(dataset['Fare_log']< 3.2),'Fare_log'] = 2
dataset.loc[dataset['Fare_log']>=3.2,'Fare_log'] = 3
train['Fare_log'].value_counts()g. 客舱
有无客舱
# 若无客舱标为0,有客舱标记为1
for dataset in full_data:
dataset['Has_Cabin'] = dataset['Cabin'].apply(lambda i: 0 if type(i)==float else 1)
train[['Has_Cabin','Survived']].groupby(['Has_Cabin'], as_index=False).sum().sort_values(by='Survived',ascending=False)
train[['Has_Cabin','Survived']].groupby(['Has_Cabin'], as_index=False).mean().sort_values(by='Survived',ascending=False)| Has_Cabin | Survived | |
|---|---|---|
| 0 | 0 | 206 |
| 1 | 1 | 136 |
| Has_Cabin | Survived | |
|---|---|---|
| 1 | 1 | 0.666667 |
| 0 | 0 | 0.299854 |
拥有客舱的乘客存活率明显高于没有客舱的乘客。
客舱分类和数值化:
Cabin里的C123此处的C代表甲板等级Deck:
# U代表Unknown没有cabin的
deck = {'A':1,'B':2,'C':3,'D':4,'E':5,'F':6,'G':7,'U':8}
for dataset in full_data:
dataset['Cabin']=dataset['Cabin'].fillna('U')
dataset['Deck']=dataset['Cabin'].map(lambda x: re.compile('[A-Za-z]+').search(x).group())
dataset['Deck']=dataset['Deck'].map(deck)
dataset['Deck']=dataset['Deck'].fillna(0)
dataset['Deck']=dataset['Deck'].astype(int)
train['Deck'].value_counts()
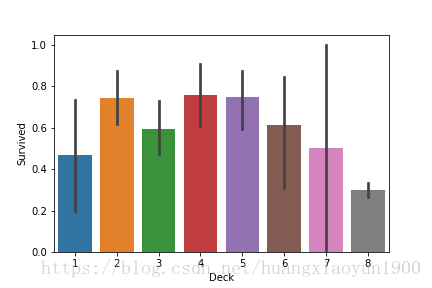
sns.barplot(x='Deck',y='Survived',data=train,order=[1,2,3,4,5,6,7,8])8 687
3 59
2 47
4 33
5 32
1 15
6 13
7 4
0 1由以上图表,将Deck分为三类:
for dataset in full_data:
dataset.loc[(dataset['Deck']<=1),'Deck']=1
dataset.loc[(dataset['Deck']>1)&(dataset['Deck']<7),'Deck']=0
dataset.loc[(dataset['Deck']>=7),'Deck']=2
train[['Deck','Survived']].groupby('Deck',as_index=False).mean().sort_values(by='Survived',ascending=False)| Deck | Survived | |
|---|---|---|
| 0 | 0 | 0.690217 |
| 1 | 1 | 0.437500 |
| 2 | 2 | 0.301013 |
h. 上船地点
for dataset in full_data:
# 缺失值填充为'S'
dataset['Embarked']=dataset['Embarked'].fillna('S')
# 数值化
dataset['Embarked']=dataset['Embarked'].map({'S': 1, 'C':2, 'Q':3}).astype(int)
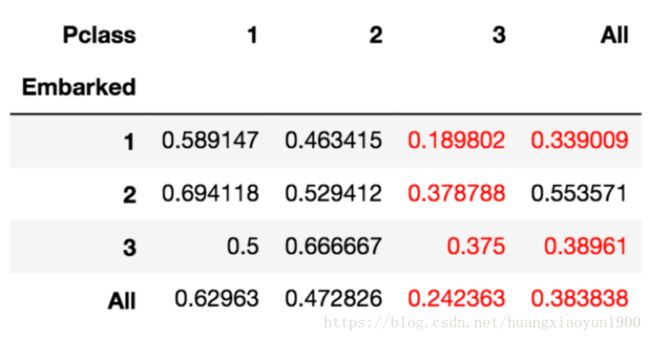
train_pivot = pd.pivot_table(train, index='Embarked', columns = 'Pclass', values = 'Survived', aggfunc=np.mean, margins=True)
def train_nagetive_red(val):
color = 'red' if val < 0.4 else 'black'
return 'color: %s'%color
train_pivot = train_pivot.style.applymap(train_nagetive_red)
train_pivot可以看到,无论从哪里上船,三等舱的乘客生存率都小于0.4;此外,若不考虑客舱等级,从S和Q上船的乘客生存率要小于从C上船的乘客。
i. 乘客的title
# 用正则表达式寻找Name里的Title
def get_title(name):
# Mr. Miss.等
title_search = re.search('([A-Za-z]+)\.',name)
if title_search:
# 返回找到的第一个字符串group(1)
return title_search.group(1)
return ""
for dataset in full_data:
dataset['Title']=dataset['Name'].apply(get_title)
f, ax = plt.subplots(1,figsize=(18,6))
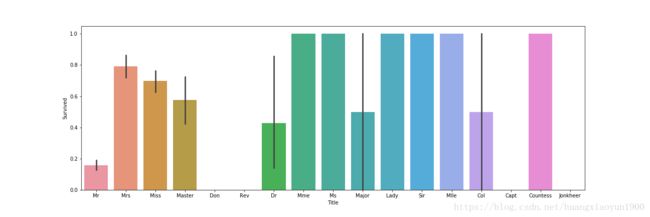
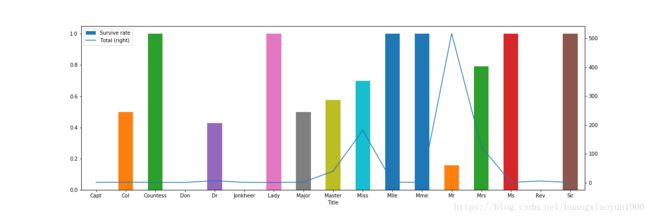
sns.barplot(x='Title',y='Survived',data=train,ax=ax)由上图可以看到不同Title之间生存率有明显差别,其中,Mme,Ms,Lady,Sir,Mlle,Countess的生存率为100%,但是单从上图中无法得出这些人的生存几率就是高于其他人,因为很可能这些人的样本数非常少,是个例。因此,需要结合总人数来看:
A = train[['Title','Survived']].groupby('Title').mean()
B = train[['Title','Survived']].groupby('Title').count()
C = pd.concat([A,B],axis=1)
C.columns = ['Survive rate','Total']
f,ax = plt.subplots(figsize=(18,6))
C.plot(kind='bar',x=C.index,y='Survive rate',ax=ax)
C.plot(kind='line',x=C.index,y='Total',secondary_y=True,ax=ax)| Survive rate | Total | |
|---|---|---|
| Title | ||
| Capt | 0.000000 | 1 |
| Col | 0.500000 | 2 |
| Countess | 1.000000 | 1 |
| Don | 0.000000 | 1 |
| Dr | 0.428571 | 7 |
| Jonkheer | 0.000000 | 1 |
| Lady | 1.000000 | 1 |
| Major | 0.500000 | 2 |
| Master | 0.575000 | 40 |
| Miss | 0.697802 | 182 |
| Mlle | 1.000000 | 2 |
| Mme | 1.000000 | 1 |
| Mr | 0.156673 | 517 |
| Mrs | 0.792000 | 125 |
| Ms | 1.000000 | 1 |
| Rev | 0.000000 | 6 |
| Sir | 1.000000 | 1 |
结合总人数来看生存率,这些生存率为100%的Title总人数都不多于2人,当然,也有些人数和生存率均很高的Title,例如,Mrs/Miss/Master,而总体来看,Mr的生存率非常低。
要使用监督学习模型,需对Title进行分类和数值化:
- Mme, Ms, Lady, Sir, Mlle, Countess: 100%.
- Mrs, Miss: around 70% survival
- Master: around 60%
- Dr, Major, Col: around 40%
- Mr: below 20%
- Don, Rev, Capt, Jonkheer: 0
for dataset in full_data:
dataset['Title']=dataset['Title'].replace(['Mme', 'Ms', 'Lady', 'Sir', 'Mlle', 'Countess'],'MMLSMC')
dataset['Title'] = dataset['Title'].replace(['Mrs', 'Miss'], 'MM')
dataset['Title'] = dataset['Title'].replace(['Dr', 'Major', 'Col'], 'DMC')
dataset['Title'] = dataset['Title'].replace(['Don', 'Rev', 'Capt', 'Jonkheer'],'DRCJ')
# title map
title_mapping = {"MMLSMC":1,"MM":2,"Master":3,"DMC":4,"Mr": 5,"DRCJ":6}
dataset['Title']=dataset['Title'].map(title_mapping)
# test中有一个“Dona.”没有赋值,取中间的值赋予它
test['Title']=test['Title'].fillna(4)
train[['Title','Survived']].groupby(['Title'],as_index=False).mean().sort_values(by='Survived',ascending=False)| Title | Survived | |
|---|---|---|
| 0 | 1 | 1.000000 |
| 1 | 2 | 0.736156 |
| 2 | 3 | 0.575000 |
| 3 | 4 | 0.454545 |
| 4 | 5 | 0.156673 |
| 5 | 6 | 0.000000 |