matlab实现loop细分
可能利用opengl实现loop细分的工作还要再搁置一段时间,先放matlab写好的程序
作者是Jesus Mena,代码在https://cn.mathworks.com/matlabcentral/fileexchange/24942-loop-subdivision中
具体的细分规则在我的http://blog.csdn.net/lafengxiaoyu/article/details/51524302这篇文章的下半篇里有很明确的简介,这里主要讲的是实现方法
首先是以loopSubdivision命名的.m文件
function [newVertices, newFaces] = loopSubdivision(vertices, faces)
% Mesh subdivision using the Loop scheme.
%
% Dimensions:
% vertices: 3xnVertices
% faces: 3xnFaces
%
% Author: Jesus Mena
global edgeVertice;
global newIndexOfVertices;
newFaces = [];
newVertices = vertices;
nVertices = size(vertices,2);
nFaces = size(faces,2);
edgeVertice = zeros(nVertices, nVertices, 3);
newIndexOfVertices = nVertices;
% ------------------------------------------------------------------------ %
% create a matrix of edge-vertices and the new triangulation (newFaces).
% computational complexity = O(3*nFaces)
%
% * edgeVertice(x,y,1): index of the new vertice between (x,y)
% * edgeVertice(x,y,2): index of the first opposite vertex between (x,y)
% * edgeVertice(x,y,3): index of the second opposite vertex between (x,y)
%
% 0riginal vertices: va, vb, vc, vd.
% New vertices: vp, vq, vr.
%
% vb vb
% / \ / \
% / \ vp--vq
% / \ / \ / \
% va ----- vc -> va-- vr --vc
% \ / \ /
% \ / \ /
% \ / \ /
% vd vd
for i=1:nFaces
[vaIndex, vbIndex, vcIndex] = deal(faces(1,i), faces(2,i), faces(3,i));
vpIndex = addEdgeVertice(vaIndex, vbIndex, vcIndex);
vqIndex = addEdgeVertice(vbIndex, vcIndex, vaIndex);
vrIndex = addEdgeVertice(vaIndex, vcIndex, vbIndex);
fourFaces = [vaIndex,vpIndex,vrIndex; vpIndex,vbIndex,vqIndex; vrIndex,vqIndex,vcIndex; vrIndex,vpIndex,vqIndex]';
newFaces = [newFaces, fourFaces];
end;
% ------------------------------------------------------------------------ %
% positions of the new vertices
for v1=1:nVertices-1
for v2=v1:nVertices
vNIndex = edgeVertice(v1,v2,1);
if (vNIndex~=0)
vNOpposite1Index = edgeVertice(v1,v2,2);
vNOpposite2Index = edgeVertice(v1,v2,3);
if (vNOpposite2Index==0) % boundary case
newVertices(:,vNIndex) = 1/2*(vertices(:,v1)+vertices(:,v2));
else
newVertices(:,vNIndex) = 3/8*(vertices(:,v1)+vertices(:,v2)) + 1/8*(vertices(:,vNOpposite1Index)+vertices(:,vNOpposite2Index));
end;
end;
end;
end;
% ------------------------------------------------------------------------ %
% adjacent vertices (using edgeVertice)
adjVertice{nVertices} = [];
for v=1:nVertices
for vTmp=1:nVertices
if (vvTmp && edgeVertice(vTmp,v,1)~=0)
adjVertice{v}(end+1) = vTmp;
end;
end;
end;
% ------------------------------------------------------------------------ %
% new positions of the original vertices
for v=1:nVertices
k = length(adjVertice{v});
adjBoundaryVertices = [];
for i=1:k
vi = adjVertice{v}(i);
if (vi>v) && (edgeVertice(v,vi,3)==0) || (viv2Index) % setting: v1 <= v2
vTmp = v1Index;
v1Index = v2Index;
v2Index = vTmp;
end;
if (edgeVertice(v1Index, v2Index, 1)==0) % new vertex
newIndexOfVertices = newIndexOfVertices+1;
edgeVertice(v1Index, v2Index, 1) = newIndexOfVertices;
edgeVertice(v1Index, v2Index, 2) = v3Index;
else
edgeVertice(v1Index, v2Index, 3) = v3Index;
end;
vNIndex = edgeVertice(v1Index, v2Index, 1);
return;
end 这里涉及到非常多很新奇的数据结构和代码思想,这段代码我得一句一句解释
global edgeVertice;
global newIndexOfVertices;
newFaces = [];
newVertices = vertices;
nVertices = size(vertices,2);
nFaces = size(faces,2);
edgeVertice = zeros(nVertices, nVertices, 3);
newIndexOfVertices = nVertices;意思是新的边点和顶点索引
值得注意的是 在函数文件里,全局变量的定义语句应放在变量使用以前,为了便于了解所有的全局变量,一般把全局变量的定义语句放在文件的前部。
注意:全局变量在使用时都需要用global来定义。也就是,在所有需要用到此全局变量的函数中都要先用global来定义了,然后再使用。
因此在后面的函数里再次定义的这两个全局变量
后面两句是初始化新面和新边
然后是计算点数和面数(2表示计算的是列)
size(A,n)如果在size函数的输入参数中再添加一项n,并用1或2为n赋值,则 size将返回矩阵的行数或列数。其中r=size(A,1)该语句返回的时矩阵A的行数, c=size(A,2) 该语句返回的时矩阵A的列数。
edgeVertice = zeros(nVertices, nVertices, 3);是非常重要的一步,建立了一个n*n*3的矩阵,n为点数,之后将展现强大的功用
% ------------------------------------------------------------------------ %
% create a matrix of edge-vertices and the new triangulation (newFaces).
% computational complexity = O(3*nFaces)
%
% * edgeVertice(x,y,1): index of the new vertice between (x,y)
% * edgeVertice(x,y,2): index of the first opposite vertex between (x,y)
% * edgeVertice(x,y,3): index of the second opposite vertex between (x,y)
%
% 0riginal vertices: va, vb, vc, vd.
% New vertices: vp, vq, vr.
%
% vb vb
% / \ / \
% / \ vp--vq
% / \ / \ / \
% va ----- vc -> va-- vr --vc
% \ / \ /
% \ / \ /
% \ / \ /
% vd vd 把一个三角形分割为四个(apr,bpq,cqr,pqr)
for i=1:nFaces
[vaIndex, vbIndex, vcIndex] = deal(faces(1,i), faces(2,i), faces(3,i));
vpIndex = addEdgeVertice(vaIndex, vbIndex, vcIndex);
vqIndex = addEdgeVertice(vbIndex, vcIndex, vaIndex);
vrIndex = addEdgeVertice(vaIndex, vcIndex, vbIndex);
fourFaces = [vaIndex,vpIndex,vrIndex; vpIndex,vbIndex,vqIndex; vrIndex,vqIndex,vcIndex; vrIndex,vpIndex,vqIndex]';
newFaces = [newFaces, fourFaces];
end;[Y1, Y2, Y3, ...] = deal(X1, X2, X3, ...) Matlab中文论坛
相当于 Y1 = X1; Y2 = X2; Y3 = X3; ...
就是把每个三角形统一化为abc,进行操作
p点是插入在a和b之间的,其对面的点是c
vpIndex = addEdgeVertice(vaIndex, vbIndex, vcIndex);
vqIndex = addEdgeVertice(vbIndex, vcIndex, vaIndex);
vrIndex = addEdgeVertice(vaIndex, vcIndex, vbIndex);function vNIndex = addEdgeVertice(v1Index, v2Index, v3Index)
global edgeVertice;
global newIndexOfVertices;
if (v1Index>v2Index) % setting: v1 <= v2
vTmp = v1Index;
v1Index = v2Index;
v2Index = vTmp;
end;
if (edgeVertice(v1Index, v2Index, 1)==0) % new vertex
newIndexOfVertices = newIndexOfVertices+1;
edgeVertice(v1Index, v2Index, 1) = newIndexOfVertices;
edgeVertice(v1Index, v2Index, 2) = v3Index;
else
edgeVertice(v1Index, v2Index, 3) = v3Index;
end;
vNIndex = edgeVertice(v1Index, v2Index, 1);
return;
end之后重新定义了两个全局变量
然后调换前两个边的顺序,使其成为顺序关系(这将为以后的运算带来方便,得到的edgeVertice矩阵将会是三角矩阵)
if (edgeVertice(v1Index, v2Index, 1)==0) % new vertex
newIndexOfVertices = newIndexOfVertices+1;这个时候就要说到edgeVertice的妙用了,其相当于有三层矩阵,每一层都是n*n,比如拿正四面体为例,一共四个点,就是4*4
就是一个4*4的表格,x行y列表示边xy
第一层表示边上插入点的索引值,例如第一次迭代为三角形123,在12上插入边,由于12这条边还没有用过,(if语句就是用来判断这条边是不是已经用过了,如果已经用过了,那么第一层的值不应该是0,第二层的值被赋予是ab边对着的点c,接下来就是赋予第三层的值,也就是ab边对着的点d【ab边只能最多被两个三角形共用,如果被一个三角形用,那其就是边界,如果被两个三角形共用,就是内部边】)
newIndexOfVertices = newIndexOfVertices+1;第二层的值被赋予是ab边对着的点c,然后返回新加入点的索引值,再对面中其他的边做
然后再遍历其他的面,如果这条边已经被其他三角形用过,第一层就不是0了,比如三角形123之后是
faces =
1 1 1 4
2 3 4 3
3 4 2 2
134,其中13已经做过了,插入的是5,对着的是2,这是插入点的索引就直接返回5,但是第三层的数加入为4
一遍做过之后
edgeVertice(:,:,1) =
0 5 7 9
0 0 6 10
0 0 0 8
0 0 0 0
edgeVertice(:,:,2) =
0 3 2 3
0 0 1 1
0 0 0 1
0 0 0 0
edgeVertice(:,:,3) =
0 4 4 2
0 0 4 3
0 0 0 2
0 0 0 0
第一个表示12间插入5,23点间插入6等
第二个表示12对着是3,23对着1等
第二个表示12还对着是4,23还对着4等
如果一条边只有对着一个点,那么对应的第三层应该是0
点的索引值搞定!下一步就是确定点的坐标
中间的一大堆代码就是干这个的
首先确定新点(就是边点坐标)
% ------------------------------------------------------------------------ %
% positions of the new vertices
for v1=1:nVertices-1
for v2=v1:nVertices
vNIndex = edgeVertice(v1,v2,1);
if (vNIndex~=0)
vNOpposite1Index = edgeVertice(v1,v2,2);
vNOpposite2Index = edgeVertice(v1,v2,3);
if (vNOpposite2Index==0) % boundary case
newVertices(:,vNIndex) = 1/2*(vertices(:,v1)+vertices(:,v2));
else
newVertices(:,vNIndex) = 3/8*(vertices(:,v1)+vertices(:,v2)) + 1/8*(vertices(:,vNOpposite1Index)+vertices(:,vNOpposite2Index));
end;
end;
end;
end;
就是这一段
遍历(n-1)*n的表格(因为第n行一定是0)
vNIndex是插入点索引
如果不为0(就是插入了点)
vNOpposite1Index = edgeVertice(v1,v2,2);
vNOpposite2Index = edgeVertice(v1,v2,3);
分别为边对着的两个点
if (vNOpposite2Index==0) % boundary case
newVertices(:,vNIndex) = 1/2*(vertices(:,v1)+vertices(:,v2));
else
newVertices(:,vNIndex) = 3/8*(vertices(:,v1)+vertices(:,v2)) + 1/8*(vertices(:,vNOpposite1Index)+vertices(:,vNOpposite2Index));之后就是计算旧点的坐标了
% ------------------------------------------------------------------------ %
% adjacent vertices (using edgeVertice)
adjVertice{nVertices} = [];
for v=1:nVertices
for vTmp=1:nVertices
if (vvTmp && edgeVertice(vTmp,v,1)~=0)
adjVertice{v}(end+1) = vTmp;
end;
end;
end;
% ------------------------------------------------------------------------ %
% new positions of the original vertices
for v=1:nVertices
k = length(adjVertice{v});
adjBoundaryVertices = [];
for i=1:k
vi = adjVertice{v}(i);
if (vi>v) && (edgeVertice(v,vi,3)==0) || (vi adjVertice{nVertices} = [];是建立了一个cell数据,为的是记录其中每个点的邻接点
比如我们这里nVertices为4,就是[] [] [] []4个数组
分别存储点1 2 3 4的邻近点
if (vvTmp && edgeVertice(vTmp,v,1)~=0) 判断是邻接点,储存入相应数组的结尾end就是数组结尾的意思,见http://blog.sina.com.cn/s/blog_6472561e0100gqqk.html
执行完这段语句之后的结果是
>>adjVertice{1}
ans =
2 3 4
>> adjVertice{2}
ans =
1 3 4
>> adjVertice{3}
ans =
1 2 4
>> adjVertice{4}
ans =
1 2 3
第二段就是分情况计算坐标了
for v=1:nVertices
k = length(adjVertice{v});
adjBoundaryVertices = [];
for i=1:k
vi = adjVertice{v}(i);
if (vi>v) && (edgeVertice(v,vi,3)==0) || (viadjBoundaryVertices = [];
for i=1:k
vi = adjVertice{v}(i);
if (vi>v) && (edgeVertice(v,vi,3)==0) || (vi然后分情况计算坐标!解释完毕
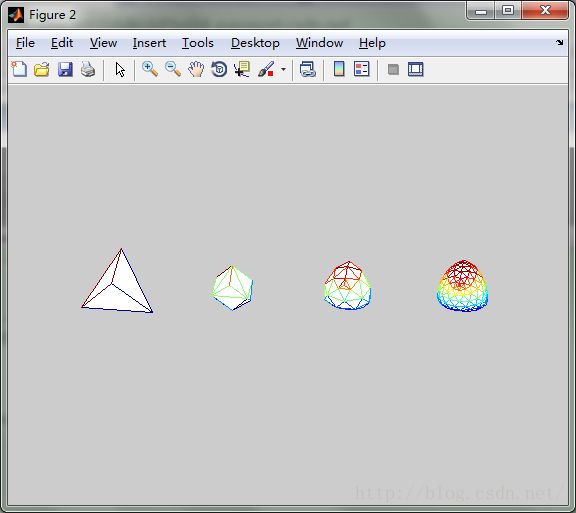
vertices = [10 10 10; -100 10 -10; -100 -10 10; 10 -10 -10]';
faces = [1 2 3; 1 3 4; 1 4 2; 4 3 2]';
figure(2);
subplot(1,4,1);
trimesh(faces', vertices(1,:), vertices(2,:), vertices(3,:));
axis tight;
axis square;
axis off;
view(3);
for i=2:4
subplot(1,4,i);
[vertices, faces] = loopSubdivision(vertices, faces);
trimesh(faces', vertices(1,:), vertices(2,:), vertices(3,:));
axis tight;
axis square;
axis off;
view(3)
end只需要说明trimesh(Tri,X,Y,Z) ,第一个tri为三角形索引,然后分别是三点x,y,z坐标