回溯法解决N皇后问题

八皇后问题

在棋盘上放置8个皇后，使得它们互不攻击，此时每个皇后的攻击范围为同行同列和同对角线，要求找出所有解。
递归函数将不再递归调用它自身，而是返回上一层调用，这种现象称为回溯（backtracking）。
当把问题分成若干步骤并递归求解时，如果当前步骤没有合法选择，则函数将返回上一级递归调用，这种现象称为回溯。 正是因为这个原因，递归枚举算法常被称为回溯法，应用十分普遍。

生成-测试法（低效）

// n皇后问题：生成-测试法
// Rujia Liu
#include
using namespace std;

// C索引表示行，值表示列
// tot表示解的个数
// nc表示执行递归函数次数
int C[50], tot = 0, n = 8, nc = 0;

void search(int cur) {
  int i, j;
  nc++;
  if(cur == n) {
    for(i = 0; i < n; i++)
      for(j = i+1; j < n; j++)
        if(C[i] == C[j] || i-C[i] == j-C[j] || i+C[i] == j+C[j]) return;
    tot++;
	// 输出正确结果
	for(int m=0; m<n; m++) {
		printf("%d", C[m]);
	}
	printf("\n");
  } else for(i = 0; i < n; i++) {
    C[cur] = i;
    search(cur+1);
  }
}

int main() {
  scanf("%d", &n);
  search(0);
  printf("%d\n", tot);
  printf("%d\n", nc);
  return 0;
}

C[i] == C[j] || i-C[i] == j-C[j] || i+C[i] == j+C[j]只比较列、主对角线、副对角线，原理见下图：

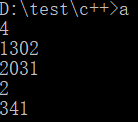
输入输出：

普通回溯法（高效）

// n皇后问题：普通回溯法
// Rujia Liu

#include
using namespace std;

int C[50], tot = 0, n = 8, nc = 0;

void search(int cur) {
  int i, j;
  nc++;
  if(cur == n) { //递归边界。 只要走到了这里，所有皇后必然不冲突
    tot++;
  } else for(i = 0; i < n; i++) {
    int ok = 1;
	//尝试把第cur行的皇后放在第i列
    C[cur] = i;
	//检查是否和前面的皇后冲突
    for(j = 0; j < cur; j++)
      if(C[cur] == C[j] || cur-C[cur] == j-C[j] || cur+C[cur] == j+C[j]) {
        ok = 0;
        break;
      }
	//如果合法，则继续递归
    if(ok) search(cur+1);
  }
}

int main() {
  scanf("%d", &n);
  search(0);
  printf("%d\n", tot);
  printf("%d\n", nc);
  return 0;
}

输入输出

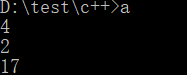
4皇后执行了17次，比生成-测试法的341次，少了不少。

优化回溯法，用二维数组判断

// n皇后问题：优化的回溯法
// Rujia Liu

#include
#include
using namespace std;

// vis表示列、主对角线、副对角线
int C[50], vis[3][50], tot = 0, n = 8, nc = 0;

void search(int cur) {
  int i, j;
  nc++;
  if(cur == n) {
    tot++;
  } else for(i = 0; i < n; i++) {
	//利用二维数组直接判断
    if(!vis[0][i] && !vis[1][cur+i] && !vis[2][cur-i+n]) {
	  //如果不用打印解，整个C数组都可以省略
      C[cur] = i;
	  //修改全局变量
      vis[0][i] = vis[1][cur+i] = vis[2][cur-i+n] = 1;
      search(cur+1);
	  //切记！一定要改回来
      vis[0][i] = vis[1][cur+i] = vis[2][cur-i+n] = 0;
    }
  }
}

int main() {
  scanf("%d", &n);
  memset(vis, 0, sizeof(vis));
  search(0);
  printf("%d\n", tot);
  printf("%d\n", nc);
  return 0;
}

如果在回溯法中使用了辅助的全局变量，一定要及时把他们恢复原状。特别的，如果函数有多个出口，则需要在每个出口初恢复被修改的值。