数据结构——AVL树(平衡二叉树)的详细实现
github地址:https://github.com/lining91/AVLTree
AVL树的介绍:
AVL树的必要条件:
1、必须是二叉查找树
2、每个节点的左子树和右子树的高度差至多为1。
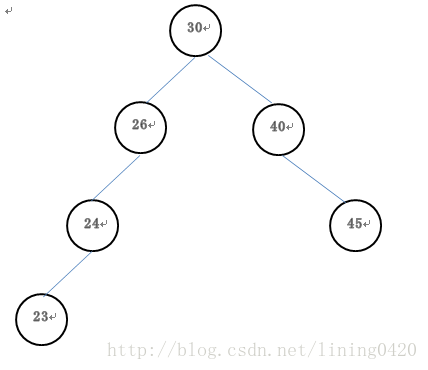
图一:非平衡二叉树
图一:非平衡二叉树中节点26的左子树高度为2,右子树高度为0,左右子树差为2。所以是非平衡二叉树。
AVL树的查找、插入、删除操作在平均和最坏的情况下都是O(logn)。
不平衡的二叉查找树在查找时效率比较低。如果需要查找的数据集合本身没有顺序,在频繁的查找的同时也经常的插入和删除的时候,AVL树是不错的选择。
相关概念:
1、平衡因子
将二叉树上节点的左子树减去右子树高度的值,称为该节点的平衡因子BF。
对于平衡二叉树,BF取值范围为[-1, 1]。对于不在此范围的树需要进行调整。
2、最小不平衡子树
距离插入节点最近的,且平衡因子的绝对值大于1的节点为根的子树。
插入新节点倒是失衡调整:
1、左单旋转
向右子树插入右孩子导致AVL失衡时,需要围绕最小失衡子树的根节点进行左单旋转。
对应接口是LeftRotaion。
2、右单旋转
向左子树插入左孩子导致AVL失衡时,需要围绕最小失衡子树的根节点进行右单旋转。
对应接口是RightRotation。
3、先左旋后右旋
在左子树上插入右孩子导致AVL树失衡时,需要进行先左旋后右旋。
对应接口是LeftRightRotation。
4、先右旋后左旋
在右子树上插入左孩子导致AVL树失衡时,需要进行先右旋后左旋。
对应接口是RightLeftRotation。
删除节点:
1、删除右子树的节点
删除右子树的节点导致AVL树失衡,相当于在左子树插入新节点导致AVL树失衡,应进行右单旋转或先右旋后左旋。
2、删除左子树的节点
删除左子树的节点导致AVL树失衡,相当于在右子树插入新节点导致AVL树失衡,应进行左单旋转或者先左旋后右旋。
查找元素:
可以使用递归和非递归两种方法查询对应的元素。
遍历:
分为先序遍历、中序遍历、后序遍历。
代码如下:
#include 
