KMP总结
什么是KMP?
KMP算法,又称为模式匹配算法,能够在线性时间内判定字符串 \(A[1\)~\(N]\) 是否为字符串 \(B[1\)~\(M]\) 的子串,并求出字符串 \(A\) 在字符串 \(B\) 中各次出现的位置。(from 李煜东《算法竞赛进阶指南》)
如何进行KMP?
第一步: \(A\)串进行自我匹配,构造出\(next\)数组
第二步: 通过\(next\)数组和\(B\)串进行匹配,构造出\(f\)数组
什么是\(next\)数组?
\(next[i]\)表示\(A[1..i]\)的前缀和后缀最大匹配的长度(且最大匹配不能为\(A\)串本身),如:(下标从\(1\)开始)
对于串 \(ababcab\)来说,\(next[7]=2\);(\(A[1..2]\)和\(A[6..7]\)均为\(ab\))
如何构造\(next\)数组?
(配合代码食用风味更佳)
代码如下:
int next[maxn+5];
void init(char A[],int n){
next[1]=0;
for(int i=2,j=0;i<=n;i++){
while(j>0&&A[i]!=A[j+1]) j=next[j];
if(A[i]==A[j+1]) j++;
next[i]=j;
}
}
十分简短的代码(虽然看不懂 (大雾))。
那么我们来看看是什么意思哈
- 首先,\(next[1]=0\),这个是显然的(定义),所以\(i\)直接从\(2\)开始;
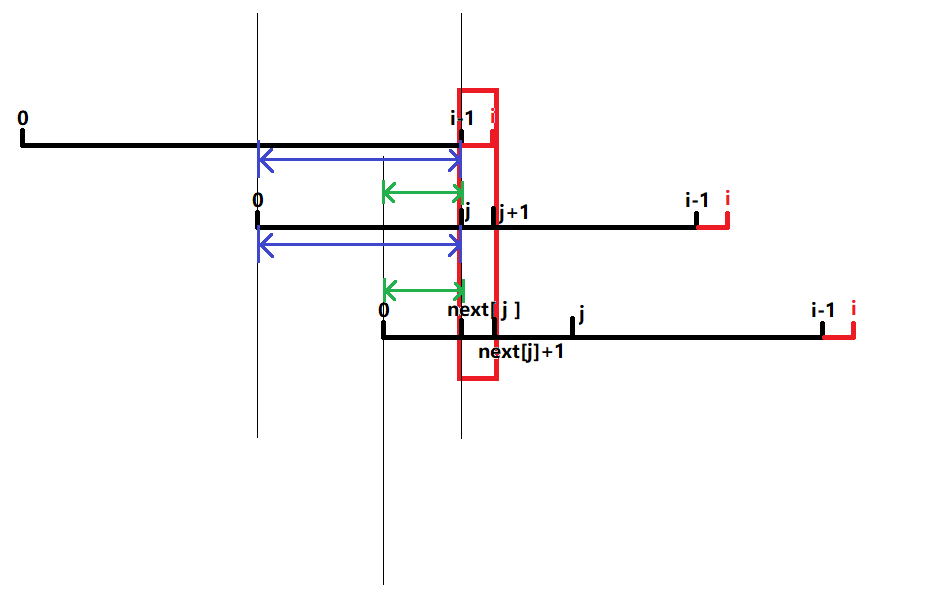
- 接下来,就是上图的过程了;
- 对于每一次循环,\(j\)的初始值都等于\(next[j-1]\);
- 在第一次\(while\)中,根据定义可得\(A[i-next[i-1] .. i-1]\)与\(A[1 .. next[i-1]]\)相等(图中蓝色区间);于是\(A[i-next[next[i-1]]..i-1]\)与\(A[1..next[next[i-1]]\)(新的前后缀)相等(图中的绿色区间)
- 之后在每一次\(while\)循环中,由于\(A[i-j .. i-1]\)与\(A[1 .. j]\)相等,所以只用判断\(A[i]\)与\(A[j+1]\)相不相等了;也只有\(A[i-j .. i-1]\)与\(A[1 .. j]\)相等才有可能匹配。所以,只有\(j=next[i]/next[next[i]]/...\)才可能符合条件。
从某种意义而言,\(next\)数组的构造,就是模式串\(A\)自我匹配的一个过程
什么是\(f\)数组?
\(f[i]\)表示\(A\)串的前缀和\(B[1..i]\)的后缀最大匹配的长度,如:(下标从\(1\)开始)
对于串\(A="abb"\)串 \(B="ababcab"\)来说,\(f[7]=2\);(\(A[1..2]\)和\(B[6..7]\)均为\(ab\))
如何构造\(f\)数组?
构造\(f\)数组的过程,和构造\(next\)数组的过程类似。(本质上是一样的)
话不多说,上代码:
int f[maxn+5];
void solve(char A[],int n,char B[],int m){
for(int i=1,j=0;i<=m;i++){
while(j>0&&(j==n||B[i]!=A[j+1])) j=next[j];
if(B[i]==A[j+1]) j++;
f[i]=j;
}
}
(还是看不懂)
(不如感性理解)
KMP的应用
事实上,\(f\)数组的构造只是其一个功能,如果将\(solve\)函数的一些部分进行更改,就可以用来解决一些特殊的问题。
在此不多赘述(我懒得写)