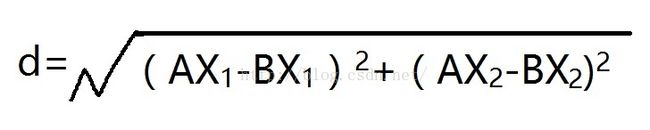KNN算法思想与应用例子
这篇文章是在学习KNN时写的笔记,所参考的书为《机器学习实战》,希望深入浅出地解释K近邻算法的思想,最后放一个用k近邻算法识别图像数字的例子。
KNN算法也称K近邻,是一种监督学习算法,即它需要训练集参与模型的构建。它适用于带标签集的行列式(可理解为二维数组)的数据集。
需要准备的数据有:训练数据集,训练标签集(每个数据与每个标签都一一对应)用于参与模型构建;需要测试的数据集——通过这个模型得出——标签集(每个数据对应的标签)
举个例子:我们把人体的指标量化,比如体重多少,三围多少,脂肪比例多少,然后这个标签就是性别(男或女)。我们的训练数据集就是500个男性和500个女性的身体指标,每个数据对应性别标签(男或女),这个就是训练标签集。然后我们输入一个人的指标,模型给出一个性别的判断,这个就是输出的标签集,也就是最后的预测结果。
算法的流程为:
1、计算输入测试数据与训练数据集的距离,这里用欧式距离来计算。
2、根据得到的距离大小,按升序排序
3、取前K个距离最小的数据集对应的标签
4、计算这些标签的出现频率
5、取出现频率最高的标签作为输入的测试数据的最后的标签,即预测结果
这个公式怎么理解呢?假设输入的被测数据为A,它有两个维度(或者说字段),分别是AX1和AX2。B为训练数据集,同理也有两个维度,BX1和BX2和,所以以上的计算公式即不同维度的差的平方的和的开方。
下面直接贴上代码,每一段都附有注释,希望童鞋们可以通过理解代码的执行来掌握整个KNN算法的流程。
# KNN算法主程序
def knnmain(inX,dataset,labels,k): #输入量有(被测数据,训练数据集,训练标签集,K值),输入量皆为数组形式
datasetsite=dataset.shape[0] #取训练数据集的总数量n
inXdata=tile(inX,(datasetsite,1)) #将被测数据的数组复制为n行相同数组组成的二维数组,方便下面的欧式距离计算
sqdistance=inXdata-dataset #开始计算欧式距离,这里计算被测数据和训练数据集之间相同维度的差
distance=sqdistance**2 #计算差的平方
dist=distance.sum(axis=1) #计算不同维度的差的平方的总和
lastdistance=dist**0.5 #将总和开方
sortnum=lastdistance.argsort() #返回从小到大(增序)的索引值
countdata={} #创建一个空字典用于储存标签和对应的数量值
for i in range(k):
vlabels=labels[sortnum[i]] #将前k个距离最近的数据的标签传给vlabels
countdata[vlabels]=countdata.get(vlabels,0)+1 #vlabels作为字典的键,而其出现的次数作为字典的值
sortnumzi=sorted(countdata.iteritems(),key=operator.itemgetter(1),reverse=True) #将字典按值降序排序,即第一位是出现次数最多的标签
return sortnumzi[0][0] #返回出现次数最多的标签值
整个KNN算法的核心思想是比较简洁的,下面贴一个手写数字识别的应用。
一个文本文档里储存一个32*32的由1和0组成的图像,差不多是下图所示:
我们大概能识别出第一个图片里是0,第二个图片里是1,实际上每个文本文档都有一个文档名,如第一个图片的文档名就是"0_0.txt",那么我们就可以从文档名里取得该图片的标签。我们有一个训练文件夹,里面的文档文件可以获取并构成训练数据集和训练标签集。
我们也有一个测试文件夹,同理里面的文档文件也可以获取并构成测试数据集和测试标签集(拿来与预测结果做对比)。文件夹截图如下:
下面直接贴上代码帮助理解
先是一个将32*32的文本文档转化为1*1024的程序,因为我们写的KNN算法主程序是以一行为单位的。
def to_32(filename):
returnoss=zeros((1,1024))
ma=open(filename)
i=int(0)
for line in ma.readlines():
for j in range(32):
returnoss[0,i*32+j]=line[j]
i += 1
return returnoss下面是手写数字识别程序:
def distinguish():
filestrain=listdir('trainingDigits') #打开训练集文件夹
filestest=listdir('testDigits') #打开测试集文件夹
mtrain=len(filestrain) #训练集文件数量
mtest=len(filestest) #测试集文件数量
allfilestrain=zeros((mtrain,1024)) #m行1024列的矩阵
allfilestest=zeros((mtest,1024))
labelstrain=[] #创造一个空列表用于储存试验向量的标签
labelstest=[]
for i in range(mtrain):
nametrain=filestrain[i] #选取文件名
inX=open('trainingDigits/%s' % nametrain)
allfilestrain[i,:]=to_32(inX) ##把每个文件中的32*32矩阵转换成1*1024的矩阵
label1=nametrain.split('.')[0]
label1=int(label1.split('_')[0]) #获取每个数据的标签
labelstrain.append(label1) #将所有标签合成一个列表
for j in range(mtest):
nametest=filestest[j]
inY=open('trainingDigits/%s' % nametest)
allfilestest[j,:]=to_32(inY)
label2=nametest.split('.')[0]
label2=int(label2.split('_')[0])
labelstest.append(label2)
labelstrain=np.array(labelstrain)
labelstest=np.array(labelstest)
grouptrain=allfilestrain
grouptest=allfilestest
error=0.0 #初始化判断错误率
results=[]
for line in grouptest:
result=knnmain(line,grouptrain,labelstrain,3)
results.append(result)
errornum=0 ##初始化判断错误数量
print 'the wrong prodiction as:'
for i in range(mtest):
if results[i] != labelstest[i]:
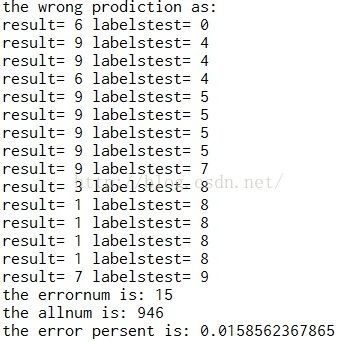
print 'result=',results[i],'labelstest=',labelstest[i] #输出所有判断错误的例子
errornum +=1
print 'the errornum is:',errornum #输出判断错误量
print 'the allnum is:',mtest #输出总测试量
error=float(errornum/float(mtest))
print 'the error persent is:',error #输出总测试错误率我们看到错误率是比较低,说明该算法的精度是很高的。
结语:从上面例子的应用来看,KNN算法的精度是很高,但是对噪声有些敏感,我们观察上面的运行结果,凡是判断失误的一般是两个数字长得比较像,比如9和5,下面的勾很像,9和7,也是比较像的,也就是说,假如测试的数据有些偏于常态,可能一个7长得比较歪,那就判断为9了,这些都是噪声,它对这些噪声的数据是无法精准识别的,因为k值较小,下面会说到k值得取值问题。另有,它的计算相对复杂,若对象数据集巨大,则计算量也很大。当然,最重要的一点,对k值的把握很重要,这一般是根据具体情况来判断,较大的k值能减少噪声干扰,但会使分类界限模糊,较小的k值又容易被噪声影响。一般取一个较小的k值,再通过交叉验证来选取最优k值。