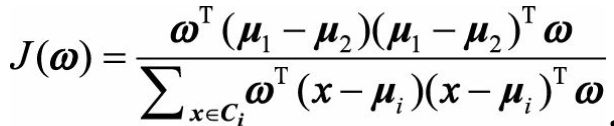机器学习--降维总结--PCA\LDA\SVD

本文部分参考和摘录了以下文章，在此由衷感谢以下作者的分享！
https://zhuanlan.zhihu.com/p/77151308
周志华老师的西瓜书
百面机器学习

开始咯！

降维

什么是降维呢，可以想象一个5 * 4矩阵乘以一个4 * 3 的一个矩阵，相当于对5 * 4的矩阵进行了线性变换，得到一个5 * 3的一个矩阵，他的维度就变成了5*3。
那么降维有什么好处呢，我们为什么要进行降维？在我们进行机器学习任务的时候，数据的维度往往很大，在进行处理和训练的时候要花费大量的时间。而这些数据中往往包含很多的冗余与噪声，如果我们能用一个低纬度的向量表示原来高纬度的特征，那我们就能节省不必要的资源。

PCA

PCA（Principal Components Analysis），主成分分析，这是一种线性、非监督、全局的降维算法。PCA的思想就是希望降维后保留尽量多的信息，但是这些信息又尽可能不相关。

你可以想像一个m*n的数据集，m为样本的数量，n为描述样本的特征的数量，我们希望降维后信息尽可能的保留，就是保留尽可能多的样本，因为降维后样本又可能会重合，这样就是失去一些样本。并且我们又希望特征变量之间不存在相关性，因为如果两个特征相关意味着他们并不是完全独立，必然存在重复信息。

为了避免降维之后的样本重合，我们希望降维后的样本尽可能的分散，而我们知道，数值上的分散程度可以用方差来描述。

那么降维后变量的相关性独立我们又怎么来描述呢，这时我们可以使用协方差来表示。为了让降维尽量的低，我们希望降维后的特征之间不存在相关性。

致此，我们就得到了降维的优化目标：将一组N维的向量降维到K维后，各变量两两协方差为0，而变量的协方差尽可能大。

为了计算方便，我们将变量均值化为0，均值化为0后，方差和协方差变为

协方差矩阵：
设

可以看出来，协方差矩阵对角线上是每个变量的方差，其余元素为两两变量的协方差。

假设原始矩阵为X，P是一组基，Y = PX，Y为X对P做基变换（降维）后的数据，Y的协方差矩阵为

因为D除了对角线外全为0，所以我们要找的P要能使C可以对角化，剩下来的就是求对角矩阵的问题啦。
找到对角矩阵后，我们将特征值按从大到小排列，选择前K大的特征值和他们对应的特征向量，这些特征向量乘以X就得到X从N维降到K维的矩阵啦。

LDA

LDA（Linear Discriminant Analysis）与PCA不同的是，LDA是一种有监督的机器学习方法，在PCA中，算法没有考虑数据的标签，只是把数据映射到一些方差比较大的方向而已。

那么LDA是怎么做的，才能使得在降维的过程中不损失类别信息？
主要的思路是希望多数据降维后，同样类别的点尽可能的接近，而异类的点尽可能的远离。对于新样本，对其降维后。

设w（w为正交基）为投影方向，u₁、u₂是某一变量特征的不同类别（C₁,C₂,假设是二分类）的均值，我们希望投影后两类的距离尽可能大
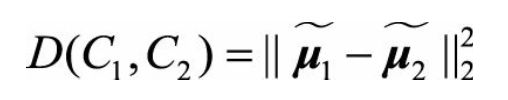（上边戴帽子的u₁、u₂的是两类中心在w方向的投影。）

而投影后两个类别各自的点距离尽可能的小，就是单独类别的点尽可能的聚集，我们想到介绍PCA时用到的方差，来描述点的分散程度。
w为单位向量。D₁，D₂分别表示两类投影后的方差

这时我们可以得出我们的优化目标

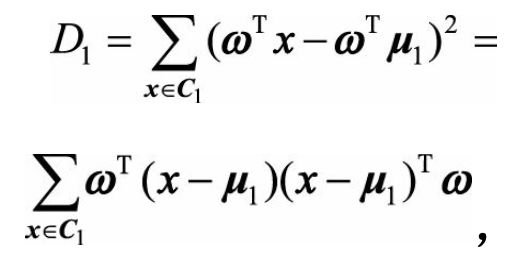
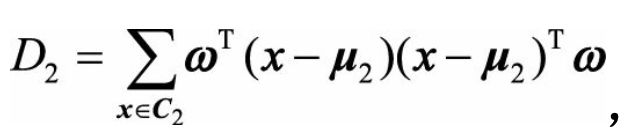
我们定义：
类内散度矩阵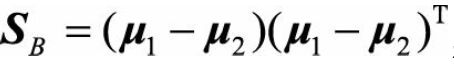
类间散度矩阵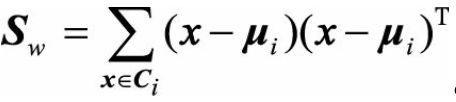
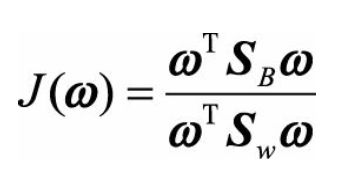我们需要最大化J(w)，对其求导，可以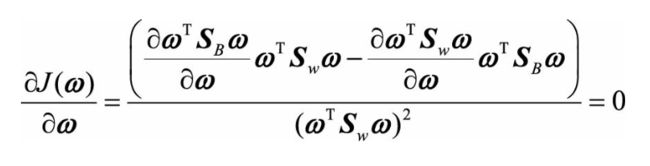得到得到
因为在二分类中w^TS_Bw^T和w^TS_ww^T是两个数我们另$\lambda$=J(w)，整理得到

S _Bw = $\lambda$S _wwf
S ^-1 _wS _Bw = $\lambda$w

这时候我们看出来，我们的目标函数转化为求一个矩阵的特征值，J(w)对应了矩阵S^-1_wS_Bw前K大特征值，而投影方向就是这个特征值对应的特征向量。

PCA与LDA的比较

从上边的推导来看，PCA与LDA其实还是有着很大的相似性，目标函数最后都转为求矩阵的特征值和特征向量，而PCA是尽量的往方差大的方向投影，而LDA是希望投影后类内的方差，而类间的方差大。
LDA是监督学习，PCA是无监督学习。
看到有个例子举得挺好的，在语音识别领域，如果单纯用PCA降维，则可能功能仅仅是过滤掉了噪声，还是无法很好的区别人声，但如果有标签识别，用LDA进行降维，则降维后的数据会使得每个人的声音都具有可分性，同样的原理也适用于脸部特征识别。

SVD

SVD，奇异值分解，是矩阵分解的一种方法，我们学高代的时候求解特征值特征向量也是一种矩阵分解的方法（EVD，特征值分解），但是这种方法只能针对实对称矩阵 nn，对与mn的矩阵可以使用SVD来进行分解。
（其实sklearn里的PCA就是用SVD来求解的）

对于矩阵A_m*n:

A _m*n=U _m*m· $\sum$ _m*n·V _n*n

U的正交向量为左奇异向量，V的正交向量为右奇异向量，U^T·U=E，V^T·V=E，$\sum$为m*n矩阵，除了对角线元素外全为0，对角线上元素为奇异值（哈哈啊哈，我把他理解为特征值之类的不过分把。）

求解：
我们知道A·A^T是实对称矩阵，

A·A ^T=U $\sum$ V ^TV $\sum$ ^T U ^T = U ^T $\sum$ $\sum$ ^TU
A ^TA=V $\sum$ ^TU ^TU $\sum$V ^T=V $\sum$ ^T $\sum$V ^T

这里要注意 $\sum$^T$\sum$和$\sum$ $\sum$^T并不相等，$\sum$^T$\sum$$\in$R^m*m，$\sum$ $\sum$^T$\in$R^n*n，

奇异值的求解
1、A^T的特征值矩阵是奇异值矩阵的平方，

$\sigma$ = $\lambda$ _i ^1/2

2、A = U$\sum$V^T$⟹$AV=U$\sum$$⟹$ Av_i = $\sigma$u_i$⟹$$\sigma$_i = Av_i / u_i

为什么要进行奇异值分解呢？
如果按照$\sum$中的奇异值从大到校排列，大多数情况下，前10%甚至1%的奇异值的和就占了全部奇异值的99%以上，一次我们可以选前k大的奇异值来描述矩阵

A _m*n $\approx$U _m*k $\sum$ _k*k V _r*n ^T

其实就是降维的作用.

致此总结了降维的一些方法和原理，有总结得不对的地方，请大家指出，一起交流一起进步。

常总结，常进步。