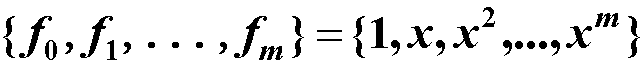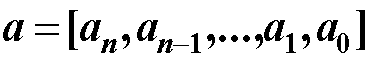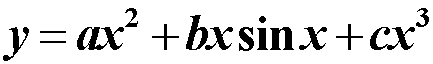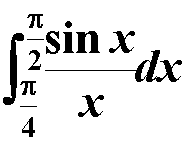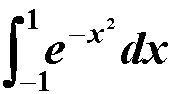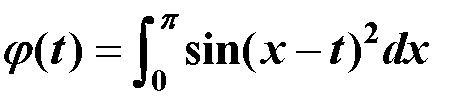matlab数值计算
第一节 多项式运算
一、多项式的表示、求值、求根
1. 表示: matlab中把多项式表达成一个行向量,该向量中的元素是按多项式降幂排列的。
显示多项式的数学形式: p1=poly2str(p,'x') 如:p=[1,2,3,4] p1=poly2str(p,'x') 结果:p1 = x^3 + 2 x^2 + 3 x + 4
2. 求多项式在某点的值的函数:polyval(p,x) p:多项式对应的行向量, x:待求值的点
p=[2,3,-1,4,5] x=[1,2,-3,5] y=polyval(p,x)
3 . 求多项式p的的根 m=roots(p)
如:p=[-1,2,3,1] x=roots(p)
二、多项式的运算
1. 四则运算
加减法:p1+p2 ; p1-p2
乘法:用卷积函数conv来实现 如:p1=[1,0,-2,-5]; p2=[2,3,1]; conv(p1,p2)
除法:用deconv来实现 对于任意两个多项式p1, p2, deconv(p1,p2)的值为两个行向量, 即[q,r]=deconv(p1,p2), 其中q是p1除以p2的商, r是余, 它们满足p1=conv(p2,q)+r.
如:p1=[1,0,-2,-5]; p2=[2,1]; [q,r]=deconv(p1,p2)
2. 求导、积分运算
求多项式p的导数:polyder(p)
求多项式p的不定积分:polyint(p) polyint(p,a,b) 非定积分
polyder(a,b): 求多项式a,b乘积的导数
polyint(a,b): 求多项式a,b乘积的积分
3. 特征多项式运算
(1)当x为行向量时,poly(x) 构造以x为根的多项式 如:x=[-1,2,3] q=poly(x)
(2)当A为方阵时, poly(A) 构造以A的特征多项式。
第二节 多项式拟合
一、数据拟合:
问题的提法:已知曲线上n个点(xi,yi), (i=1,2,…,n), xi互不相同,寻求一个函数y=F(x), 使y=F(x)在某种准则下与所有数据点最为接近,即曲线拟合得最好。
基本思路:对n个点构成的数据集{(xi,yi), i=1,2,…,n}, m为小于n的整数,设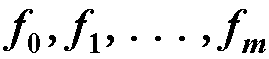 是m+1个线性无关的连续函数(称为基本拟合函数),取
是m+1个线性无关的连续函数(称为基本拟合函数),取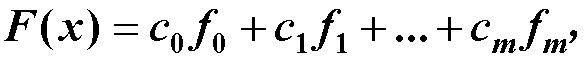 按准则
按准则 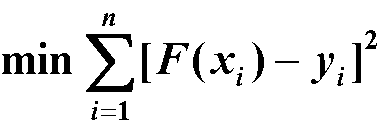 确定常数
确定常数 (最小二乘法)
(最小二乘法)
按此方法得到的函数 称为数据集(xi,yi), i=1,2,…,n的最小二乘拟合函数。
称为数据集(xi,yi), i=1,2,…,n的最小二乘拟合函数。
衡量拟合情况优劣的指标有:
(1)SSE(误差平方和)The sum of squares due to error 该统计参数计算的是拟合数据和原始数据对应点的误差的平方和: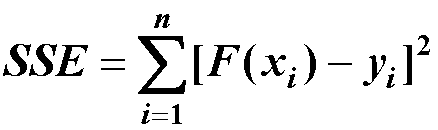
SSE越接近于0,说明模型选择和拟合效果好,数据预测也成功。下面的指标MSE和RMSE与指标SSE有关联,它们的校验效果是一样的。
(3)RMSE(剩余标准差)Root mean squared error 该统计参数,也叫回归系统的拟合标准差,是MSE的平方根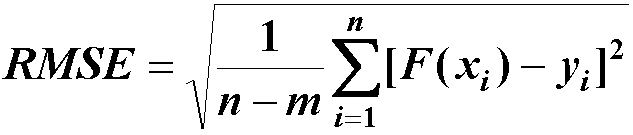
(4)R-square(判断系数,拟合优度)Coefficient of determination,判断系数是由两个参数SSR和SST决定的,对总平方和 进行分解有SST =SSE +SSR,
进行分解有SST =SSE +SSR, 其中SSE 是误差平方和,反映随机误差对 y 的影响, SSR 称为回归平方和,反映自变量对y 的影响。判断系数定义为
其中SSE 是误差平方和,反映随机误差对 y 的影响, SSR 称为回归平方和,反映自变量对y 的影响。判断系数定义为 若它接近1,表示F(x)能较好的拟合该数据集。
若它接近1,表示F(x)能较好的拟合该数据集。
(5)调整的判断系数 统计学家主张在回归建模时,应采用尽可能少的自变量,不要盲目地追求判定系数 R2 的提高。 其实,当变量增加时,残差项的自由度就会减少。而自由度越小,数据的统计趋势就越不容易显现。 为此,又定义一个调整判定系数: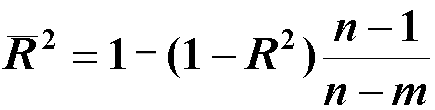
当 n 很大、 m 很少时,两者之间的差别不是很大;但是,当 n 较少,而m 又较大时, 就会远小于
就会远小于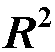
二、多项式拟合
即用m次多项式拟合给定数据,称多项式拟合。
Matlab中的多项式拟合函数:polyfit
格式:a=polyfit(x,y,n) x:横坐标 y:纵坐标
功能:对一组点(x,y)进行n次多项式拟合。
x,y为要拟合的数据, n为拟合多项式的次数,
拟合多项式在x处的值可用polyval(a,x)计算
可进入拟合工具箱cftool(x,y)处理数据拟合问题。 例1 对x=0:0.1:1; y=[-0.447,1.978,3.11,5.25,5.02,4.66,4.01,4.58,3.45,5,35,9.22] 求三次拟合多项式。
解 x=0:0.1:1;
y=[-0.447,1.978,3.11,5.25,5.02,4.66,4.01,4.58,3.45,5.35,9.22];
p=polyfit(x,y,3)
xx=0:0.01:1;
yy=polyval(p,xx);
plot(xx,yy,'-b',x,y,'.r','markersize',20) t=0:1:15;
y=[30.0 29.1 28.8 28.1 28.0 27.7 27.5 27.2 27.0 26.8 26.5 26.3 26.1 25.7 25.3 24.8];
plot(t,y,'r*')
A=polyfit(t,y,3)
tt=0:0.5:15;
z=polyval(A,tt);
plot(t,y,'r*',tt,z,'b')对数据求出合适次数的拟合多项式p(x),由弧长公式: 得对河底光缆长度的估计s, 所需光缆为s+y(0)+y(20) 6次多项式拟合较为合适。光缆总长:46.28m
得对河底光缆长度的估计s, 所需光缆为s+y(0)+y(20) 6次多项式拟合较为合适。光缆总长:46.28m
x=0:1:20;
y=[-9.2,-8.91,-8.02,-7.95,-8.11,-9.05,-10.12,-11.08,-12.25,-13.26,-13.45,-12.62,-11.28,-10.23,-9.25,-7.91,-8.05,-8.86,-9.85,-10.81,-10.96];
polytool(x,y,3)
n=input('拟合次数n=')
format long
p=polyfit(x,y,n)
dp=polyder(p)
x1=0:0.01:20;
y1=sqrt(1+polyval(dp,x1).^2);
s=trapz(x1,y1)-y(1)-y(end)
第三节 非线性拟合
问题的提法:设非线性函数其中是未知参数由实验获得该函数数据点 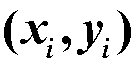
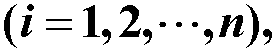 ,确定参数
,确定参数 ![]() 。
。
1. 非线性拟合函数:lsqcurvefit
格式:[x, resnorm,r,flag]=lsqcurvefit(fun, x0,xdata,ydata) x0为初始解向量;xdata,ydata为满足关系ydata=F(x, xdata)的数据; fun为待拟合函数, resnorm=sum ((fun(x,xdata)-ydata).^2),即在x处残差的平方和; r=fun(x,xdata)-ydata,即在x处的残差; flag为终止迭代的条件
xdata = [3.6,7.7,9.3,4.1,8.6,2.8,1.3,7.9,10.0,5.4];
ydata = [16,150.5,260.1,22.5,206.5,9.9,2.7,165.5,325.0,54.5];
解法:定义函数 f=@(a,x) a(1)*x.^2 + a(2)*x.*sin(x) + a(3)*x.^3;
由 [a, resnorm,r]=lsqcurvefit(f, a0,xdata,ydata)确定参数,画图观察拟合效果
2. 用fittype函数做曲线拟合
使用fittype函数可以自定义拟合函数,可以满足线性拟合和非线性拟合。fittype函数具有很灵活的配置,基本满足各种复杂场景。 使用方法:
(1)做多项式拟合
p=fittype('poly2')
f=fit(x,y,p)
plot(f,x,y)
如:对下列数据做多项式拟合 x=[1;1.5;2;2.5;3]; y=[0.9;1.7;2.2;2.6;3];
x=[1;1.5;2;2.5;3];
y=[0.9;1.7;2.2;2.6;3];
p=fittype('poly2')
f=fit(x,y,p)
plot(f,x,y)
(2)做非线性拟合
方法1:(线性化方式)
如: ex= {'x.^2', ‘sin(x)','1'}; f=fittype(ex)
实验:x=[0.2,0.5,0.8,1.1,1.2,1.5,1.8,2]; y=[2.35,1.38,0.81,0.62,0.78,1.43,2.25,3.18];
方法2:(非线性化方式) 如:p=fittype(‘a*x.^2+b*sin(x)+c’,‘independent’,‘x’)
clc,clear
x=[0,0.4,1.2,2,2.8,3.6,4.4,5.2,6,7.2,8,9.2,10.4,11.6,12.4,13.6,14.4,15]';
y=[1,0.85,0.29,-0.27,-0.53,-0.4,-0.12,0.17,0.28,0.15,-0.03,-0.15,-0.07,0.059,0.08,0.032,-0.015,-0.02]';
f=fittype('a*cos(k*x)*exp(w*x)','independent','x');
cfun=fit(x,y,f)
xi=0:0.1:20;
yi=cfun(xi);
plot(x,y,'r*',xi,yi,'b-')
第四节 插值问题
一、一元函数插值
已知n+1个节点时,可得n次拉格朗日插值多项式。
若F(x)为分段函数,称为分段插值; 插值中使用较多的是分段线性插值和三次样条插值。
分段线性插值
设函数y=f(x)的插值节点为(xi,yi), (i=0,1,2, …,n) 将每两个相邻的节点用直线连起来,如此形成的一条 折线就是分段线性插值函数记为:In(x), 它满足In(xi)=yi ,且在每个小区间上是一次函数。
分段线性插值具有收敛性: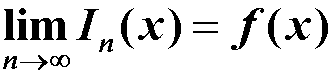 但在节点处In(x)不可导,光滑性较差。
但在节点处In(x)不可导,光滑性较差。
Matlab中的一维插值函数interp1
格式1:yi=interp1(x,y,xi) 功能:已知函数y=f(x)的一组插值节点(x,y),求出其插值函数F(x)在点xi处的函数值yi。
格式2:yi=interp1(y,xi) 默认x=1:n,n为向量y的元素个数。
格式3:yi=interp1(x,y,xi,’method’)
Method:
(1)nearest 线性最近项插值
(2)linear 线性插值
(3)spline 三次样条插值
(4)cubic 立方插值
缺省时默认为为分段线性插值
例1 通过实验测得某函数的一组数据如下: x: 0,3,5,7,9,11,12,13,14,15 y: 0,1.2,1.65,2.1,2.15,2.0, 1.85,1.65,1.55,1.25 试作出其插值函数的图形
x=[0,3,5,7,9,11,12,13,14,15];
y=[0,1.2,1.65,2.1,2.15,2.0,1.85,1.65,1.55,1.25];
xi=0:0.1:15;
yi=interp1(x,y,xi,'spline');
yi1=interp1(x,y,xi,'linear');
yi2=interp1(x,y,xi,'cubic');
plot(x,y,'*',xi,yi,'r-',xi,yi1,‘b-',xi,yi2,‘g-')
legend('节点','三次样条插值','线性插值','立方插值')
三次样条插值是解决一维插值问题最常用的方法, Matlab中实现三次样条插值的方法有:
(1)yi=interp1(x,y,xi,’spline’)
(2)使用spline函数:
用法1:yi=spline(x,y,xi)(缺点:找不到方程表达式) 效果同(1)
用法2:pp=spline(x,y)
获得三次样条插值的分段多项式pp, 可使用ppval计算插值。
(3)使用csape函数:
用法: pp=csape(x,y) 可以添加参数选择边界条件。
例2 通过实验测得某函数的一组数据如下: x: 0,3,5,7,9,11,12,13,14,15 y: 0,1.2,1.65,2.1,2.15,2.0,1.85,1.65,1.55,1.25 试作出其插值函数的图形。
x=[0,3,5,7,9,11,12,13,14,15];
y=[0,1.2,1.65,2.1,2.15,2.0,1.85,1.65,1.55,1.25];
xi=0:0.1:15;
yi=interp1(x,y,xi,'spline');
yi1=interp1(x,y,xi,'linear');
yi2=interp1(x,y,xi,'cubic');
plot(x,y,'*',xi,yi,'r-',xi,yi1,‘b-',xi,yi2,‘g-') legend('节点','三次样条插值','线性插值','立方插值')
//
clear,clc
x=[0,3,5,7,9,11,12,13,14,15];
y=[0,1.2,1.65,2.1,2.15,2.0,1.85,1.65,1.55,1.25];
xi=0:0.1:15;
S=csape(x,y)
%Sa=spline(x,y)
P=S.coefs
% Pa=Sa.coefs(系数信息)
yi=ppval(S,xi);
plot(x,y,'o',xi,yi,'r');
二、 二元函数插值
1. 网格节点数据插值函数:interp2
格式:z=interp2(x0,y0,z0,x,y,’method’)
x0,y0,z0(横纵竖):插值节点坐标,要求x0,y0单调;
x,y是被插值点的横坐标与纵坐标( x,y不能超过x0,y0的范围),z是被插值点的函数值。
Method:(1)nearest 最邻近插值 (2)linear 双线性插值 (3)cubic双三次插值 默认为双线性插值。
| 4800 |
1350 |
1370 |
1390 |
1400 |
1410 |
960 |
940 |
880 |
800 |
690 |
570 |
430 |
290 |
210 |
150 |
| 4400 |
1370 |
1390 |
1410 |
1430 |
1440 |
1140 |
1110 |
1050 |
950 |
820 |
690 |
540 |
380 |
300 |
210 |
| 4000 |
1380 |
1410 |
1430 |
1450 |
1470 |
1320 |
1280 |
1200 |
1080 |
940 |
780 |
620 |
450 |
370 |
350 |
| 3600 |
1420 |
1430 |
1450 |
1480 |
1500 |
1550 |
1510 |
1430 |
1300 |
1200 |
980 |
850 |
750 |
550 |
500 |
| 3200 |
1430 |
1450 |
1460 |
1500 |
1550 |
1600 |
1550 |
1600 |
1600 |
1600 |
1550 |
1500 |
1500 |
1550 |
1500 |
| 2800 |
950 |
1190 |
1370 |
1500 |
1200 |
1100 |
1550 |
1600 |
1550 |
1380 |
1070 |
900 |
1050 |
1150 |
1200 |
| 2400 |
910 |
1090 |
1270 |
1500 |
1200 |
1100 |
1350 |
1450 |
1200 |
1150 |
1010 |
880 |
1000 |
1050 |
1100 |
| 2000 |
880 |
1060 |
1230 |
1390 |
1500 |
1500 |
1400 |
900 |
1100 |
1060 |
950 |
870 |
900 |
930 |
950 |
| 1600 |
830 |
980 |
1180 |
1320 |
1450 |
1420 |
1400 |
1300 |
700 |
900 |
850 |
840 |
380 |
780 |
750 |
| 1200 |
740 |
880 |
1080 |
1130 |
1250 |
1280 |
1230 |
1040 |
900 |
500 |
700 |
780 |
750 |
650 |
550 |
| 800 |
650 |
760 |
880 |
970 |
1020 |
1050 |
1200 |
830 |
800 |
700 |
300 |
500 |
550 |
480 |
350 |
| 400 |
510 |
620 |
730 |
800 |
850 |
870 |
850 |
780 |
720 |
650 |
500 |
200 |
300 |
350 |
320 |
| 0 |
370 |
470 |
550 |
600 |
670 |
690 |
670 |
620 |
580 |
450 |
400 |
300 |
100 |
150 |
250 |
| y/x |
0 |
400 |
800 |
1200 |
1600 |
2000 |
2400 |
2800 |
3200 |
3600 |
4000 |
4400 |
4800 |
5200 |
5600 |
clear,clc
load data404
x=0:400:5600; y=4800:-400:0;
[X,Y]=meshgrid(x,y);
surf(X,Y,Z)(原始数据的图形)
pause
figure(2)
xi=linspace(0,5600,80);(取80个节点)
yi=linspace(0,4800,80);
[Xi,Yi]=meshgrid(xi,yi);
Zi=interp2(X,Y,Z,Xi,Yi);
surf(Xi,Yi,Zi)
pause
figure(3)
t=0:100:1600; (画等高线)
[c,h]=contourf(Xi,Yi,Zi,t);
clabel(c,h)(标上等高线)
colormap cool(加色调)
colorbar(加色标)2. 散点数据插值函数:griddata 已知n个插值节点(xi,yi,zi), (i=1,2,…,n), 求在点(x,y)处的插值z, matlab提供函数griddata。
格式:cz=griddata(x,y,z,cx,cy,’method’)
其中x,y,z 均为n 维向量,指明所给数据点(插值节点)的横坐标、纵坐标和竖坐标。 cx,cy是给定被插值点的横坐标和纵坐标,cz为相应点的竖坐标。
若cx,cy是向量,则给定以它们所确定网格点的横坐标和纵坐标,这时要求cx,cy一个为行向量一个为列向量。 编程时也可先用meshgrid将cx,cy定义成网格矩阵。
clear ,clc
x=[129,140,103.5,88,185.5,195,105,157.5,107.5,77,81,162,162,117.5];
y=[7.5,141.5,23,147,22.5,137.5,85.5,-6.5,-81,3,56.5,-66.5,84,-33.5];
z=-[4,8,6,8,6,8,8,9,9,8,8,9,4,9];
[x1,y1]=meshgrid(75:5:200,-50:5:150);
z1=griddata(x,y,z,x1,y1,’v4’);
surf(x1,y1,z1)
figure(2)
[c,h]=contourf(x1,y1,z1);
clabel(c,h)
第五节 数值积分
一、数值积分的常用方法
(1)用梯形法计算积分, 适用于被积函数为离散数据时, 求函数的定积分。 该函数调用格式:I=trapz(x,y)(分点越密效果越好)
clc,clear
format long
ac=@(x)sin(x)./x
x1=pi/4:pi/50:pi/2;
y1=ac(x1);
s1=trapz(x1,y1)
x2=pi/4:pi/100:pi/2;
y2=ac(x2);
s2=trapz(x2,y2)
(2) 基于变步长辛普森法计算积分(了解) quad或quadtx,
调用格式: [I,n]=quad(‘fname’,a,b,Tol,trace)
其中:‘fname’是被积函数名。
a,b是积分上下限。
Tol是精度控制值,省却时取0.001
Trace:控制是否显示展现积分过程,取0不展现
I:积分值(返回量)
n:被积函数调用次数
如:求积分: ac=@(x)sin(x)./x s=quad(ac,pi/4,pi/2)
ac=@(x)sin(x)./x s=quad(ac,pi/4,pi/2)
如:求积分: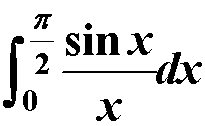 ac=@(x)sin(x)./x s=quad(ac, realmin(最小正实数),pi/2)
ac=@(x)sin(x)./x s=quad(ac, realmin(最小正实数),pi/2)
x=1:0.05:20;
n=length(x);
f=@(t)sin(t)./t;
for i=1:n
y(i)=quad(f,0,x(i));
end
plot(x,y)
(3) 高精度Lobatto积分法, 格式:z = quadl(Fun,a,b)
(4) 自适应Gauss-Kronrod数值积分法 z = quadgk(Fun,a,b)
f=@(x)exp(-x.^2)
y1=quadl(f,-1,1)
y2=quadgk(f,-1,1)
(5) 积分法矢量化自适应simpson数值积分 格式:z = quadv(Fun,a,b) 一次可以计算多个积分
如:求积分: F=@(x,n)1./((1:n)+x.^2); quadv(@(x)F(x,6),0,1)
F=@(x,n)1./((1:n)+x.^2); quadv(@(x)F(x,6),0,1)
clc,clear
f=@(x,t)sin((x-t).^2);
t=-5:0.05:5;
n=length(t);
for i=1:n
s(i)=quad(f,0,pi,[],[],t(i));
end
plot(t,s)