《OpenCV3编程入门》第5章-学习笔记6.3-离散傅里叶变换-dft（）函数（代码示例）

先准备一些必要知识：

《OpenCV3编程入门》第5章-学习笔记6.2-离散傅里叶变换-DFT()函数使用方法及准备知识 

//--------------------------------------【程序说明】-------------------------------------------
//		                               离散傅里叶变换，单通道图像
//------------------------------------------------------------------------------------------------


//---------------------------------【头文件、命名空间包含部分】-----------------------------
//		描述：包含程序所使用的头文件和命名空间
//-------------------------------------------------------------------------------------------------
#include "opencv2/core/core.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/highgui/highgui.hpp"
#include 
using namespace cv;


//--------------------------------------【main( )函数】-----------------------------------------
//          描述：控制台应用程序的入口函数，我们的程序从这里开始执行
//-------------------------------------------------------------------------------------------------
int main()
{

	//【1】以灰度模式读取原始图像并显示
	Mat srcImage = imread("pic.jpg", 0);
	if (!srcImage.data) { printf("读取图片错误，请确定目录下是否有imread函数指定图片存在~！ \n"); return false; }
	imshow("原始图像", srcImage);


	//【2】将输入图像延扩到最佳的尺寸，边界用0补充
    //目的是为了图像变成2,3,5倍数，加快计算速度
	int m = getOptimalDFTSize(srcImage.rows);
	int n = getOptimalDFTSize(srcImage.cols);
	//将添加的像素初始化为0.
	Mat padded;
	copyMakeBorder(srcImage, padded, 0, m - srcImage.rows, 0, n - srcImage.cols, BORDER_CONSTANT, Scalar::all(0));

	//【3】为傅立叶变换的结果(实部和虚部)分配存储空间。
    //傅里叶结果是复数，对于每个原图像值，结果会有2个图像值
    //此外，频值范围远大于空间值范围，所以存在float格式，并增加一个通道存储复数部分
	//将planes数组组合合并成一个多通道的数组complexI
	Mat planes[] = { Mat_(padded), Mat::zeros(padded.size(), CV_32F) };
	Mat complexI;
	merge(planes, 2, complexI);

	//【4】进行就地离散傅里叶变换，输入输出都是一副图
	dft(complexI, complexI);

	//【5】将复数转换为幅值，即=> log(1 + sqrt(Re(DFT(I))^2 + Im(DFT(I))^2))
	split(complexI, planes); // 将多通道数组complexI分离成几个单通道数组，planes[0] = Re(DFT(I), planes[1] = Im(DFT(I))
	magnitude(planes[0], planes[1], planes[0]);// planes[0] = magnitude  
	Mat magnitudeImage = planes[0];

	//【6】进行对数尺度(logarithmic scale)缩放
    //傅里叶变换幅度值范围大道不适合在屏幕显示，高值为白点，低值为黑点，所以对数变换尺度
	magnitudeImage += Scalar::all(1);
	log(magnitudeImage, magnitudeImage);//求自然对数

	//【7】剪切和重分布幅度图象限
    //将第二步中延展的图像，新添加的像素剔除
	//若有奇数行或奇数列，进行频谱裁剪      
	magnitudeImage = magnitudeImage(Rect(0, 0, magnitudeImage.cols & -2, magnitudeImage.rows & -2));
	//重新排列傅立叶图像中的象限，使得原点位于图像中心  
	int cx = magnitudeImage.cols / 2;
	int cy = magnitudeImage.rows / 2;
	Mat q0(magnitudeImage, Rect(0, 0, cx, cy));   // ROI区域的左上
	Mat q1(magnitudeImage, Rect(cx, 0, cx, cy));  // ROI区域的右上
	Mat q2(magnitudeImage, Rect(0, cy, cx, cy));  // ROI区域的左下
	Mat q3(magnitudeImage, Rect(cx, cy, cx, cy)); // ROI区域的右下
	//交换象限（左上与右下进行交换）
	Mat tmp;
	q0.copyTo(tmp);
	q3.copyTo(q0);
	tmp.copyTo(q3);
	//交换象限（右上与左下进行交换）
	q1.copyTo(tmp);
	q2.copyTo(q1);
	tmp.copyTo(q2);

	//【8】归一化，用0到1之间的浮点值将矩阵变换为可视的图像格式
	//此句代码的OpenCV2版为：
	//normalize(magnitudeImage, magnitudeImage, 0, 1, CV_MINMAX); 
	//此句代码的OpenCV3版为:
	normalize(magnitudeImage, magnitudeImage, 0, 1, NORM_MINMAX);

	//【9】显示效果图
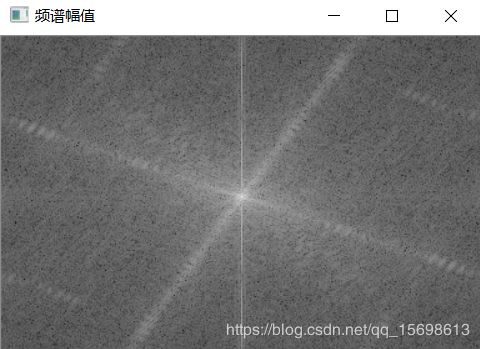
	imshow("频谱幅值", magnitudeImage);
	waitKey();

	return 0;
}

运行结果：

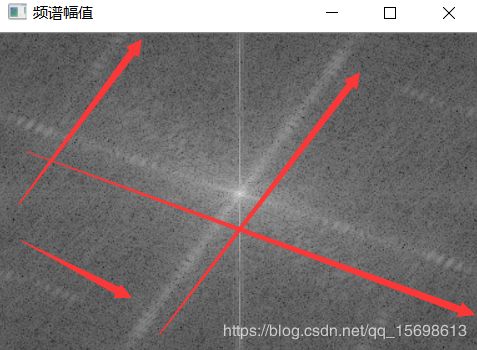
 结果分析：

频谱幅值显示了图片在频率域上的表象特征，如箭头所示，对比原始图片，发现确实如此！