阿里2018校园招聘 研发工程师（一）选择题自总

1.一台机器对200个单词进行排序花了200秒(使用冒泡排序)，那么花费800秒，大概可以对多少个单词进行排序

   A400       B500      C600      D700      E800      F900

 

思路：首先要知道冒泡排序的时间复杂度是O(n^2)

答案是A

 

2.设一棵二叉树有 3 个叶子节点，有 8 个度为 1 的节点，则该二叉树中总的节点数为______。

   A12      B13      C14      D15       E16      F17

 

思路：二叉树结点的度数指该结点所含子树的个数，二叉树是每个结点最多有两个子树的有序树(即度最多等于2)。

           关于度的计算，有这样一个公式：N2=N0-1，度为2的节点个数是度为0的节点个数减一。

           故在本题中，叶子节点不包含子树，说明在这棵二叉树中度为0的节点有三个。那么根据公式可以推出度为2的节点数N2=3-1=2。得Nsum = N2+N1+N0 = 2+3+8=13

正解为B

 

3.在一个axb的整数矩阵中，寻找最长的严格递减数字序列。数列可以沿着横或竖的方向，但不能重叠，该问题的最优复杂度是____。举例来说，以下是一个3x5的矩阵，其结果如下：

        AO(M*N)      BO(M+N)      CO(Mlogn)      DO(N*logM)      EO(M^2*N^2)      FO(max(M,N))

思路：此题通过分析可得四个选项里的M，N，指的是矩阵的M行和N列，从算法角度考虑，若想寻找最长的严格的递减数字序列，应该从某个元素作为当前值开始找起，比较当前值横竖方向上的比当前值小且与当前值差值最小的值作为下一个当前值进行遍历，再接着进行如上的操作判断，直到所有元素都遍历一遍，在遍历的过程中，如果某个元素作为当前值遍历过了，就做好标记，下一次就不再遍历了。

哔哔了这么多，就一句话，要是想要找出严格递减数字序列，那么最好的情况下（比如题目中给的例子，就是最好的情况下），每个元素也是都要至少遍历一次的（作为当前值比较一次），那么就是程序运行过程中，都要至少遍历M*N个元素，即执行M*N次操作。

故时间复杂度为O(M*N)

正解为A

 

4.考虑以下二分查找的代码：

#include 
int bsearch(int array[], int n, int v)
{
    int left, right, middle;
    left = 0, right = n - 1;
    while (left <= right) {
        middle = left + (right - left) / 2;
        if (array[middle] > v ) {
            right = middle;
        } else if (array[middle] < v) {
            left = middle;
        } else {
            return middle;
        }
  } 
    return -1;
}

对于输入array为：{2, 6, 8, 10, 13, 25, 36, 45, 53, 76, 88, 100, 127}， n = 13, v = 127时,
运行bsearch函数，while循环调用的次数为____。

         A1      B3      C4      D5      E6      F无数次

思路：

在取整的过程中会出现每次取整后Middle值不变的情况。

选 无数次。

经推算：

第一次middle=6；

第二次middle=9；

第三次middle=10；

第四次middle=11；

之后由于middle=11+（12-11）/2=11,middle值一直没有变化，所以为无数次

正解：F

 

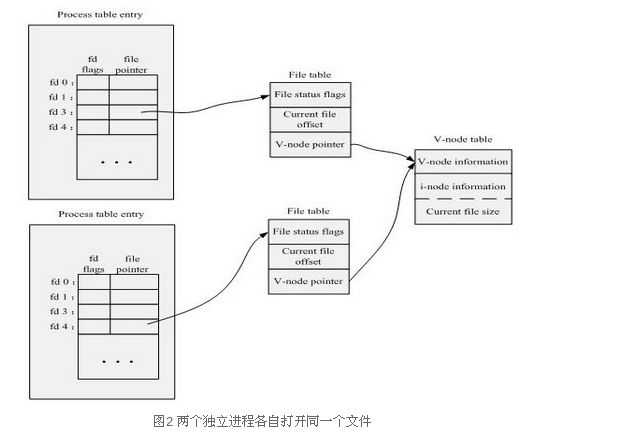
5.Linux下两个进程可以同时打开同一个文件，这时如下描述错误的是：

           A两个进程中分别产生生成两个独立的fd

           B两个进程可以任意对文件进行读写操作，操作系统并不保证写的原子性

          C进程可以通过系统调用对文件加锁，从而实现对文件内容的保护

          D任何一个进程删除该文件时，另外一个进程会立即出现读写失败

          E两个进程可以分别读取文件的不同部分而不会相互影响

         F一个进程对文件长度和内容的修改另外一个进程可以立即感知

 

思路：这需要背记
       内核中，对应于每个进程都有一个文件描述符表，表示这个进程打开的所有文件。文件描述表中每一项都是一个指针，指向一个用 于描述打开的文件的数据块———file对象，file对象中描述了文件的打开模式，读写位置等重要信息，当进程打开一个文件时，内核就会创建一个新的file对象。需要注意的是，file对象不是专属于某个进程的，不同进程的文件描述符表中的指针可以指向相同的file对象，从而共享这个打开的文件。file对象有引用计数，记录了引用这个对象的文件描述符个数，只有当引用计数为0时，内核才销毁file对象，因此某个进程关闭文件，不影响与之共享同一个file对象的进程。

       应该选D, 一般删除都是文件索引，如果两个文件同时打开同一个文件，一个线程执行删除操作，只要另一个线程不退出，就可以继续对该文件进行操作，一旦退出才找不到该文件的索引节点而报错。

正解：D

 

6.从1,2,3,......,49,50里选择一个集合S，使得若x属于S，则2x不属于S，则S最多能有____个元素。

    A25         B27          C30          D33           E36          F37

思路：首先选出26-50共25个数,肯定不会有他们的二倍的数在集合中.同时可以去掉13-25,因为他们的二倍全在26-50中。剩下1-12.此时类似原问题,选择7-12共6个数(他们的二倍已经被去掉了)。同时去掉4-6,也因为他们的二倍都在7-12中.最后可以选择1,3两个数，这样总共有25+6+2=33个

最后这个因为1*2=2，所以，选择1，3可以，选择2，3也可以。利用从后往前倒推的思路，非常的妙！

正解D

 

7.有1,2,3,......无穷个格子，你从1号格子出发，每次1/2概率向前跳一格，1/2概率向前跳两格，走到格子编号为4的倍数时结束，结束时期望走的步数为____。

   A2        B12/5          C14/5          D16/5       E18/5          F4

思路：

先补知识,在概率论和统计，数学期望（或预期值,或平均，或一个随机变量的第一时刻）是随机变量就其概率测度的积分。对于离散随机变量，这是等同于可能的值的概率加权总和。
数学期望 :
E(X) = X1*p(X1) + X2*p(X2) + …… + Xn*p(Xn)
X1,X2,X3,……,Xn为数据，p(X1),p(X2),p(X3),……p(Xn)为这几个数据的概率函数.
对于连续随机变量, 这是等同于概率密度函数的加权积分.

回到题目，跳两格都算一步；

dp(i,j)表示从格子i到格子j的期望步数：

dp(1,4)=1+0.5*dp(2,4)+0.5*dp(3,4)；

dp(2,4)=1+0.5*dp(3,4)+0.5*dp(4,4);

dp(3,4)=1+0.5*dp(4,4)+0.5*dp(1,4);

dp(4,4)=0;

求解上述方程得到dp(1,4)=18/5;

其中，1代表每次先走一步，然后再加上之后的期望。

以d(1,4)为例，d(1,4)表示的其实是，先从1位置跳到2位置，再从2位置跳到4位置或者，先从1位置跳到3位置，再从3位置跳到4位置。从2位置跳到4或者从3跳到4，就是：0.5*dp(2,4)+0.5*dp(3,4)；

那从1跳到2，或者从1跳到3，的概率总和是1。

那么在计算dp(3,4)的时候出现了d(1,4),因为题目要求走到格子编号为4的倍数时结束，其实，该写成：

d(3,4) = 0.5 + 0.5 + 0.5d(5,8)

第一个0.5指的是跳一步，正好到第四个位置；后面的0.5+0.5d(5,8)指的是跳两步，跳到第五个位置，然后，从五的位置向8跳（因为只要是4的倍数截至，都行）那d(5,8),其实可以看成是d(1,4)的循环，所以，用d(1,4)替换就行了。

正解E

 

8.凯撒（Caesar)密码是一种基于字符替换的对称式加密方法，它是通过对26个英文字母循环移位和替换来进行编码的。设待加密的消息为"Alibaba Group"，加密后的密文是"RCzsrsr XIFLG"，则采用的密匙k是____。

   A10       B11       C13      D15         E17

思路：直接对应位来看移动了几位，第一个A移动到R共移动了17位。所以k就是17.

正解E

 

9.现有1G数据需要排序，计算资源只有1G内存可用，下列排序方法中最可能出现性能问题的是____。

   A堆排序         B插入排序       C归并排序         D快速排序         E选择排序         F冒泡排序

思路：主要是考察各种排序方法的空间复杂度

          请见下表，比较可知中最可能出现性能问题的是归并排序的辅助空间为O（n）

排序法	平均时间	最差情形	稳定度	额外空间
冒泡	O(n^2)	O(n^2)	稳定	O(1)
交换	O(n^2)	O(n^2)	不稳定	O(1)
选择	O(n^2)	O(n^2)	不稳定	O(1)
插入	O(n^2)	O(n^2)	稳定	O(1)
基数	O(logRB)	O(logRB)	稳定	O(n)
Shel l	O(nlogn)~O(n^2)	O(n^s) 1	不稳定	O(1)
快速	O(nlogn)	O(n^2)	不稳定	O(logn)
归并	O(nlogn)	O(nlogn)	稳定	O(n)
堆	O(nlogn)	O(nlogn)	不稳定	O(1)

O(n)这样的标志叫做渐近时间（空间）复杂度,是个近似值.各种渐近时间（空间）复杂度由小到大的顺序如下：

                             O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)

正解C

 

10.某操作系统采用分页存储管理方式，下图给出了进程A和进程B的页表结构。如果物理页的大小为512字节，那么进程A与进程B的物理内存总共使用了____字节。

进程A页表：                         进程B页表：

逻辑页    物理页                     逻辑页    物理页

 

0            9                       0            1

 

1            2                       1            3

 

2            4                       2            4

 

3            6                       3            7

 

4                                    4            2

 

5                                    5

 

    A4608          B3584        C4096         D5120        E2560         F2048

思路：

物理页可以在进程间共享，两个进程共使用了1,2,3,4,6,7,9，共7个物理页。

故：7*512=3584

正解B

 

11.以下函数中，和其他函数不属于一类的是____。

    Afwrite       Bputc        Cpwrite        Dputchar         Egetline         Fscanf

思路：Linux下对文件操作有两种方式：系统调用(system call)和库函数调用(Library functions)。系统调用实际上就是指最底层的一个调用，在linux程序设计里面就是底层调用的意思。面向的是硬件。而库函数调用则面向的是应用开发的，相当于应用程序的api。

简明的回答是：函数库调用是语言或应用程序的一部分，而系统调用是操作系统的一部分。

本题中，pwrite是系统调用，其他都是库函数

补充：Linux中常见的系统函数：

• fcntl  文件控制  
• open  打开文件  
• creat  创建新文件  
• close  关闭文件描述字  
• read  读文件  
• write  写文件  
• readv  从文件读入数据到缓冲数组中  
• writev  将缓冲数组里的数据写入文件  
• pread 对文件随机读  
• pwrite  对文件随机写

正解C

 

12.一个英雄基础攻击力为100，携带了三件暴击武器，武器A有40%的概率打出2倍攻击，武器B有20%的概率打出4倍攻击，武器C有10%概率打出6倍攻击，各暴击效果触发是独立事件，但是多个暴击效果在一次攻击中同时触发时只有后面武器的暴击真正生效，例如一次攻击中武器A判定不暴击，武器B和武器C都判定触发暴击，那么这次攻击实际是600攻击力。那么这个英雄攻击力的数学期望是____。 

   A186.6      B200      C232.8      D256.8         E320     F332.6

思路：

参考第7题，

（600 * 10%） +（400* 90% * 20% ）+（200 * 90% * 80% * 40%） +（100*60%*80%*90%）= 232.8

正解C

 

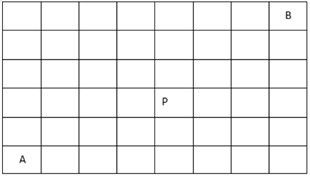
13.在如下8*6的矩阵中，请计算从A移动到B一共有____种走法。要求每次只能向上或向右移动一格，并且不能经过P。

    A456          B492      C568      D626      E680     F702

思路：

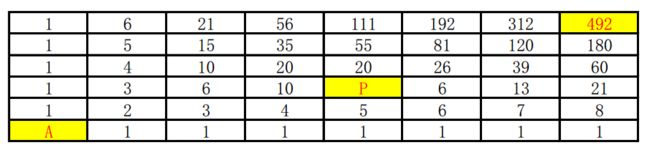
动态规划：f(x,y) = f(x,y-1) + f(x-1, y)，  这题要注意不能经过点P

笔试的时候时间有限，一个一个填还容易出错，建议打开Excel输入公式，直接拖，

效果如下：

正解B

 

14.有一个类A，其数据成员如下：

class A {
...
private:
     int a;
public:
     const int b;
     float* &c;
     static const char* d;
     static double* e;
};

则构造函数中，成员变量一定要通过初始化列表来初始化的是：______。

    Aa b c       Bb c        Cb c d e         Db c d      Eb           Fc

思路：

构造函数初始化时必须采用初始化列表一共有三种情况，  
1.需要初始化的数据成员是对象(继承时调用基类构造函数)  
2.需要初始化const修饰的类成员  
3.需要初始化引用成员数据

因为static属于类并不属于具体的对象，所以 static成员是不允许在类内初始化的，那么static const 成员是不是在初始化列表中呢？

答案是NO

一是static属于类，它在未实例化的时候就已经存在了，而构造函数的初始化列表，只有在实例化的时候才执行。

二是static成员不属于对象。我们在调用构造函数自然是创建对象，一个跟对象没直接关系的成员要它做什么呢

正解B

 

15.下面数据结构能够支持随机的插入和删除操作、并具有较好的性能的是____。

A数组和链表         B链表和哈希表           C哈希表和队列           D队列和堆栈        E堆栈和双向队列        F双向队列和数组

思路：1，数组是在定义的时候申请一块连续的内存空间，访问某个元素只需要通过下标就可以，但是随机插入和删除都要移动后面所有的元素，所以，数组肯定不行；

2，链表，是非连续的空间，通过指针访问，所以随机插入和删除通过指针之间的操作很方便，但是如果要查询一个数的时候还是得依次便利，但是题目问的是随机插入和删除，所以，链表可以；

3，栈，所有的操作都是在栈顶，如果要随机插入或者删除某个数也必须依次对其他数就行操作，所以，栈也排除；

4，队列，通过队头和队尾指针进行读入数据和删除数据，如果直接在队尾添加数据很方便，但是，题目中是随机，所以，队列排序；

5，哈希表通过键值对操作，只要知道相关的key很容易就行读取和删除，插入某个元素也通过key很方便，所以，哈希表肯定可以；

正解B

 

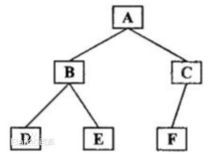
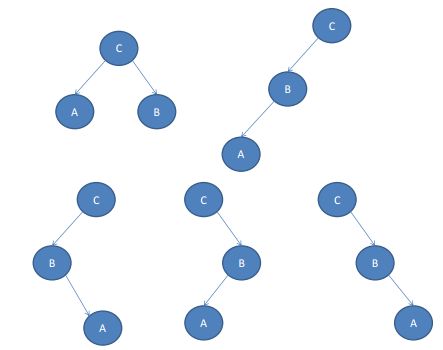
16.对一棵二叉树进行后续遍历，其输出结果为A，B，C，这样的二叉树有____棵。

     A1          B2         C3         D5           E7           F9

思路：

补后序遍历：

后序遍历结果：DEBFCA

首先，后序遍历-左右根，C必为根结点！分3种情况：

（1）A、B分别分布在左右子树 （+1）；

（2）A、B都在左子树：那么 左子树上B必为根结点，A可作其左右孩子节点都行（+2）；

（3）A、B都在右子树， 与（二）类似，（+2）

所以一共有5种！

正解D

 

17.猜数字游戏的过程是你输入一个4位数（数字选取0~9，不会重复），电脑会告诉你两个信息：A个数字和位置均正确，B个数字正确但位置错误。例如正确答案是7890你输入0789，电脑会告诉你0A4B，表示有0个数字和位置完全正确，但有4个数字正确但位置错误。现在你猜了三次的结果分别是：1234=>0A4B，2341=>1A3B，3412=>2A2B，那么最少还要猜____次才能保证一定得到4A0B的结果。

      A0         B1          C2          D3        E4           F5

思路：

分析后的结果只可能是2413、4312、3142、3421，那么我们接下来肯定要从这几个数里面猜。

假设最后的结果是3421。

(1) 我们先猜2413，会提示1A，那么就可以排除结果是3142的可能（如果是，2413会提示0A），只可能是4312和3412，那么我们猜2次或者3次就可以得到正确结果；

(2) 如果我们先猜4312，会提示0A，那么就可以排除2413和3142，只剩下3421，这样我们只需猜2次就可以确定。

(3) 如果我们先猜3142，会提示1A，那么就可以排除2413，这样我们只需猜2次或3次就可以确定。

(4) 如果我们先猜3421，会提示4A，这样我们只需猜1次就可以确定。

综上，我们要猜结果是3421，至少要猜3次就一定能保证。

同理，猜结果是2413、4312、3142也一样。

因为保证最少还要猜____次才能保证一定得到，那只有三了，因为2不一定保证一定得到。

正解D

 

18.假设淘宝网上某商品A在任一时刻t内若有人浏览，则该商品在下一时刻t+1内无人浏览的概率为0.35（即下一时刻的浏览情况仅与当前时段相关），定义此条件概率为 P(O_{t+1}=0|O_t=1)=0.35(即用“1”代表有人浏览的事件，用“0”代表无人浏览的事件），类似得定义P(O_{t+1}=1|O_t=1)=0.65，P(O_{t+1}=0|O_t=0)=0.4，P(O_{t+1}=1|O_t=0)=0.6。若此商品A在t=0时有人浏览，它在t=100000时有人浏览的概率是____。

      A0.5371           B0.4582           C0.6316          D0.1435          E0.3276            F0.7132

思路：

解：写出马尔科夫矩阵如下 

P(O_{t+1}=0|O_t=0)=0.4 
P(O_{t+1}=1|O_t=0)=0.6 
P(O_{t+1}=0|O_t=1)=0.35 
P(O_{t+1}=1|O_t=1)=0.65 
求出马尔科夫矩阵的特征值为1 对应的的特征向量为 

可知最后的稳态为无人浏览0.35/(0.35+0.6),有人浏览0.6/(0.35+0.6)。答案是C

最后附MIT线代课程中的马尔科夫矩阵的应用 

 

 ———————————————— 
版权声明：本文为CSDN博主「ls317842927」的原创文章，遵循CC 4.0 by-sa版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/ls317842927/article/details/61915708

正解C

 

19.假定CSomething是一个类，执行下面这些语句之后，内存里创建了____个CSomething对象。

CSomething a();
CSomething b(2);
CSomething c[3];
CSomething &ra = b;
CSomething d=b;
CSomething *pA = c;
CSomething *p = new CSomething(4);

     A10         B9         C8          D7          E6         F5

思路：

CSomething a();//没有创建对象，这里不是使用默认构造函数，而是定义了一个函数，在C++ Primer393页
//有说明。
CSomething b;//使用一个参数的构造函数，增加1个对象
CSomething c[3];//使用无参构造函数，对象数组，增加3个对象
CSomething &ra=b;//引用不增加对象
CSomething d=b;//调用拷贝构造函数，增加1个对象
CSomething *pA=c;//地址赋值，不增加对象
CSomething *p=new CSomething;//在堆上构造一个对象，增加1个对象

//所以最后一共有： 1+3+1+1 = 6个对象。


CSomething a();// 定义一个函数，参数为空，返回值为CSomething对象， 类似int func();  
CSomething a; // 定义对象a，使用默认构造函数CSomething::CSomething() 
CSomething a(0); // 定义对象a，使用构造函数CSomething::CSomething(int)

正解：E

 

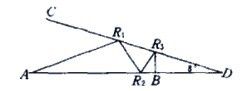
20.如图所示，从A点发出一束激光，于AD直线和CD直线反射多次后，垂直达到了B点（B点可能在AD上也可能在CD上，入射角等于反射角），如角CDA=8°，那么最多反射次数是____。（从B点原路反射回点A次数不纳入计算，图中给出3次反射的例子）

    A6                 B10               C12           D38              E40               F不存在

思路：
链接：https://www.nowcoder.com/questionTerminal/b8f1ffb25cd046c68af191f3d7f9510c
来源：牛客网
首先有题设中给出的角度可以得出初始入射角和反射角是8度，入射角和反射角之和要小于(180-8)。经反射角等于入射角以及三角形定理得知，第二次入射角和反射角为16度，第三次为24度，依次为32  40  48  56  64  72  80  88 (入射角不会大于90度) 。至此共有11次，但如果入射角为88 反射角也将为88度 此时两角之和为176  大于(180 - 8) 所以反射次数为10次

正解：B