【网络流】【树链剖分】CodeForces786E ALT

题意：

给出一棵树，有一些人要从某个点沿最短路走向另一个点，现在可以在人和边上放狗。要求：每个人要么自己有一条狗，要么经过的每一条边上都有一条狗。

---

分析：

首先，如果数据范围小一点，那么这就变成了最小割板题了：
连边方式：

那么，为了解决会T的问题，考虑优化建图。

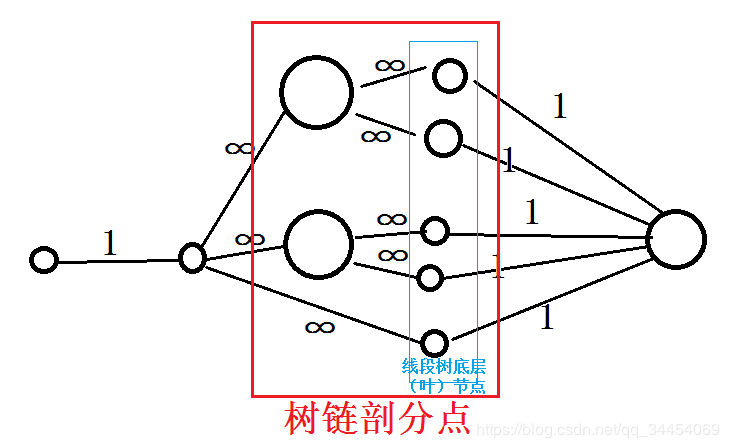
受到线段树优化区间建图的思想启发，不难联想到：用树上的线段树优化链建图：树链剖分

所以，这就是一个树链剖分优化建图的板题…

#include
#include
#include
#include
#include
#define SF scanf
#define PF printf
#define INF 0x3FFFFFFF
#define MAXN 100010
using namespace std;
struct node{
	int v,id;
	node *nxt;
}edge[MAXN];
node *head[MAXN],*ncnt=edge;
int cnt;
vector<int> a[MAXN],w[MAXN],rev[MAXN];
int n,m,tot,tot1,s,t;
void link_edge(int u,int v,int id){
	ncnt++;
	ncnt->nxt=head[u];
	ncnt->v=v;
	ncnt->id=id;
	head[u]=ncnt;
}
int dfn[MAXN],top[MAXN],fa[MAXN],siz[MAXN],dep[MAXN],son[MAXN],fai[MAXN],rnk[MAXN],num[MAXN];
void find_son(int x,int f=0){
	siz[x]=1;
	dep[x]=dep[f]+1;
	for(node *i=head[x];i!=NULL;i=i->nxt){
		int v=i->v;
		if(v==f)
			continue;
		fai[v]=i->id;
		fa[v]=x;
		find_son(v,x);
		siz[x]+=siz[v];
	}
	for(node *i=head[x];i!=NULL;i=i->nxt){
		int v=i->v;
		if(v==f)
			continue;
		if(siz[v]>siz[son[x]]||son[x]==0)
			son[x]=v;	
	}
}
void prep(int x,int tp,int f=0){
	top[x]=tp;	
	dfn[x]=++cnt;
	rnk[cnt]=x;
	if(son[x]==0)
		return ;
	prep(son[x],tp,x);
	for(node *i=head[x];i!=NULL;i=i->nxt){
		int v=i->v;
		if(v==f||v==son[x])
			continue;
		prep(v,v,x);
	}
}
void add_edge(int u,int v,int val){
//	PF("[%d --> %d : %d]\n",u,v,val);
	a[u].push_back(v);
	a[v].push_back(u);
	w[u].push_back(val);
	w[v].push_back(0);
	rev[u].push_back(a[v].size()-1);
	rev[v].push_back(a[u].size()-1);	
}
int pl[MAXN],pr[MAXN];
void build(int id,int l=1,int r=n){
	if(l==r){
		add_edge(id,t,1);
		num[id]=fai[rnk[l]];
		return ;
	}
	int mid=(l+r)>>1;
	pl[id]=++tot;
	pr[id]=++tot;
	build(pl[id],l,mid);
	build(pr[id],mid+1,r);
	add_edge(id,pl[id],INF);
	add_edge(id,pr[id],INF);
}
void add_edge_insegtree(int tar,int l1,int r1,int id=3,int l=1,int r=n){
	if(l>=l1&&r<=r1){
		add_edge(tar,id,INF);
		return ;	
	}
	int mid=(l+r)>>1;
	if(l1<=mid)
		add_edge_insegtree(tar,l1,r1,pl[id],l,mid);
	if(r1>mid)
		add_edge_insegtree(tar,l1,r1,pr[id],mid+1,r);
}
void add_edge_intree(int id,int u,int v){
	while(top[u]!=top[v]){
		if(dfn[top[u]]<dfn[top[v]])
			swap(u,v);
//		PF("--[%d(%d) %d(%d)]\n",top[u],dfn[top[u]],u,dfn[u]);
		add_edge_insegtree(id,dfn[top[u]],dfn[u]);
		u=fa[top[u]];
	}
	if(dep[u]<dep[v])
		swap(u,v);
//	PF("<%d %d>\n",u,v);
	if(u!=v)
		add_edge_insegtree(id,dfn[son[v]],dfn[u]);
}
int d[MAXN],g[MAXN];
int dfs(int x,int flw){
	if(x==t)
		return flw;
	int flw1=flw;
	for(int i=0;i<int(a[x].size());i++){
		int u=a[x][i];
		if(w[x][i]!=0&&d[u]==d[x]-1){
			int f=dfs(u,min(flw,w[x][i]));
			w[x][i]-=f;
			w[u][rev[x][i]]+=f;	
			flw-=f;
			if(flw==0)
				break;
			if(d[s]>=tot)
				return flw1-flw;
		}
	}
	if(flw!=flw1)
		return flw1-flw;
	if(g[d[x]]==1){
		d[s]=tot;
		return 0;
	}
	g[d[x]]--;
	int minh=tot;
	for(int i=0;i<int(a[x].size());i++)
		if(w[x][i]!=0)
			minh=min(minh,d[a[x][i]]);
	d[x]=minh+1;
	g[d[x]]++;
	return 0;
}
int maxflow(){
	g[0]=tot;
	int ans=0;
	while(d[s]<tot)
		ans+=dfs(s,INF);
	return ans;
}
bool vis[MAXN];
void gov(int x){
	vis[x]=1;
	for(int i=0;i<int(a[x].size());i++)
		if(w[x][i]!=0&&vis[a[x][i]]==0)
			gov(a[x][i]);
}
vector<int> dogman,dogedge;
int main(){
	SF("%d%d",&n,&m);
	int u,v;
	for(int i=1;i<n;i++){
		SF("%d%d",&u,&v);
		link_edge(u,v,i);
		link_edge(v,u,i);
	}
	find_son(1);
	prep(1,1);
	s=1;
	t=2;
	tot=2;
	build(++tot);
	tot1=tot;
	for(int i=1;i<=m;i++){
		SF("%d%d",&u,&v);
		add_edge(s,i+tot,1);
		add_edge_intree(i+tot,u,v);
	}
	tot+=m;
	PF("%d\n",maxflow());
	gov(s);
	for(int i=0;i<int(a[s].size());i++)
		if(vis[a[s][i]]==0)
			dogman.push_back(a[s][i]-tot1);
	for(int i=0;i<int(a[t].size());i++)
		if(vis[a[t][i]]==1)
			dogedge.push_back(num[a[t][i]]);
	PF("%d",int(dogman.size()));
	for(int i=0;i<int(dogman.size());i++)
		PF(" %d",dogman[i]);
	PF("\n");
	PF("%d",int(dogedge.size()));
	for(int i=0;i<int(dogedge.size());i++)
		PF(" %d",dogedge[i]);
	PF("\n");
}