C/C++经典算法

 

1. 选择排序

void selectSort(int a[], int n)
{
    int i, j;
    int min, temp;
    for (i = 0;i < n - 1; i++)
    {
        min = i;
        for (j = i + 1; j < n;j++)
        {
            if (a[j] < a[min])
                min = j;
        }
        if (min != i)
        {
            temp = a[min];
            a[min] = a[i];
            a[i] = temp;
        }
    }
}

2. 快速排序

void quickSort(int a[], int left, int right)
{
    int i = left, j = right - 1;
    int x = a[right];
    int temp;
    while (1)
    {
        while(a[i] < x)
            i++;
        while (a[j] > x)
            j--;
        if (i >= j) break;
        temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
    temp = a[i];
    a[i] = a[right];
    a[right] = temp;
    if (left < (i - 1))
        quickSort(a, left, i -1);
    if (i+1 < right)
        quickSort(a,i+1,right);
}

3. 折半查找

int binSearch(int a[], int left, int right, int k)
{
    int mid;
    if (left > right) return -1;
    else
    {
        mid = left + right;
        if (k == a[mid])
            return mid;
        if (k > a[mid])
            return binSearch(a, mid + 1, right, k);
        else
            return binSearch(a, left, mid - 1, k);
    }
}

4. 斐波那契数列第n项

//递归实现
int Fibo(int n)
{
    if (n == 1 || n == 2)
        return 1;
    else
        return Fibo(n - 1) + Fibo(n - 2);
}

//非递归实现
int Fibo_(int n)
{
    if (n == 1 || n == 2)
        return 1;
    else
    {
        int a, b = 1, c = 1;
        for (int i = 3; i <= n;i++)
        {
            a = b + c;
            c = b;
            b = a;
        }
        return a;
    }
}

5. 寻找数组中的次大数

//10个互不向等的整数，求其中的第二大的数，要求数组不能排序。

int getSecMaxVal(const int arr[], int n)
{
    int max, secmax;
    if (arr[1] > arr[0])
    {
        max = arr[1];
        secmax = arr[0];
    }
    else
    {
        max = arr[0];
        secmax = arr[1];
    }
    for (int i = 2; i < n; i++)
    {
        if (arr[i] > max)
        {
            secmax = max;
            max = arr[i];
        }
        else if (arr[i] > secmax && arr[i] < max)
            secmax = arr[i];
    }
    return secmax;
}

6. 将大于2的偶数分解成两个素数

int getPrimePair(int n)
{
    if (n <= 2 || n % 2 != 0)
        return 0;
    for (int i = 2; i < n / 2; i++)
    {
        for (int j = n / 2; j < n - 1; j++)
        {
            if (i + j == n)
            {
                if (i % 2 != 0 && j % 2 != 0)
                    cout << "(" << i << "," << j << ")" << " ";
            }
        }
    }
    cout << endl;
    return 1;
}

7. 计算一年中的第几天

int getDays(int year, int month, int date)
{
    int days = 0;
    int months[12] = { 31,0,31,30,31,30,31,31,30,31,30,31 };
    if ((year % 4 == 0 && year % 100 != 0) || year % 400 == 0)
        months[1] = 29;
    else
        months[1] = 28;
    if (month <= 0 || month > 12 || date > months[month] || date <= 0)
        return -1;
    for (int i = 0; i < month; i++)
        days += months[i];
    days += date;
    return days;
}

8. 相隔多少天

输入两天的信息（年，月，日），计算这两天之间相隔多少天。注意：这两天可以是任意的年份和任意月份。

typedef struct date
{
    int year;
    int month;
    int day;
}Date;

int getYearDays(int year_1, int year_2)
{
    int early, late;
    if (year_1 <= year_2)
    {
        early = year_1;
        late = year_2;
    }
    else
    {
        early = year_2;
        late = year_1;
    }
    int days = 0;
    for (int i = early;i < late; i++)
    {
        if ((i % 4 == 0 && i % 100 != 0) || i % 400 == 0)
            days += 366;  //闰年
        else
            days += 365; //平年
    }
    return days;
}

int getIntervalDays(Date date_1, Date date_2)
{
    int days1, days2;
    if (date_1.year < date_2.year)
    {
        days1 = getDays(date_1.year, date_1.month, date_1.day);
        days2 = getDays(date_2.year, date_2.month, date_2.day)
            + getYearDays(date_2.year,date_1.year);
    }
    else if (date_1.year > date_2.year)
    {
        days1 = getDays(date_2.year, date_2.month, date_2.day);
        days2 = getDays(date_1.year, date_1.month, date_1.day)
            + getYearDays(date_1.year, date_2.year);
    }
    else
    {
        days1 = getDays(date_2.year, date_2.month, date_2.day);
        days2 = getDays(date_1.year, date_1.month, date_1.day);
    }
    return abs(days2 - days1);
}

int main()
{
    Date date2 = { 2019,8,22 };
    Date date1 = { 2017,7,27 };
    int x = getIntervalDays(date2,date1);
    cout << x << endl;
}

9. 丢番图的墓志铭

以下数字可以告诉你他的生命有多长：六分之一是童年，再过了十二分之一，长满了胡须，又过了生命的七分之一他结婚了。婚后五年，他有了第一个孩子，但孩子只有他父亲一半的生命，儿子死后他又活了4年。

根据以上叙述可以得出一下公式：

  1 / 6 * x + 1 / 12 * x + 1 / 7 * x + 5 + 1 / 2 * x + 4 = x;

对上述一元一次方程求解即可，

float getAge()
{
    for (float age = 0.0; age < 120.0; age++)
        if (age / 6.0 + age / 12.0 + age / 7.0 + 5.0 + age / 2.0 + 4.0 == age)
            return age;
}

10. 寻找丑数

把只包含2，3，5的数称为丑数。例如6，8都是丑数，而14不是丑数，因为它包含因子7，通常也把1称为丑数。编程找出1500内的全部丑数。

这个解法的关键是任何判断丑数，根据题目，丑数只包含因子2，3，5，而不包含其他任何因子，同时1也是丑数，因此可以把一个非1的丑数形式化的表示为

UglyNumber = 2 ^ n * 3 ^ n * 5 ^ n    其中n表示n次方

不难看出，如果将丑数循环除以2，直到除不尽为至；再循环除以3，直到除不尽为止；再循环除以5，那么结果一定为1。如果按照此法循环相处最终结果不为1，则说明该数中除了包含2，3，5因子外还有其他因子，所以该数不是丑数。具体算法如下

int isUglyNumber(int number)
{
    
    while (number % 2 == 0)
        number /= 2;
    while (number % 3 == 0)
        number /= 3;
    while (number % 5 == 0)
        number /= 5;
    
    return number == 1;
}

int printUglyNumber(int limit)
{
    int count = 0;
    
    for (int i = 1; i < limit; i++)
        if (isUglyNumber(i))
        {
            count++;
            cout << i << "\t";
        }
    return count;
}

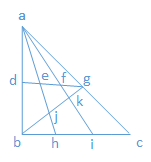
11. 编程计算下图中的三角形

使用穷举法时，首先列举出图中所有线段，然后将选出三条任意线段，判断这三条线段是否能够构成三角形。

用一个指针数组来保存所有线段：

char  * map[] = { "ab","ad","db","ag","gc","ac","ah","ae","ej","jh",
"aj","eh","af","ak","ai","fk","fi","ki","de","df","dg","ef","eg",
"fg","bj","bk","bg","jk","jg","kg","bh","bi","bc","hi","hc","ic" };

列全所有线段后，按照从上到下的的编程思想，编写函数对这些线段进行任意三条组合并判断是否是三角形。

int printTriangleNumber()
{
    int i, j, k;
    int count = 0;
    for (i = 0; i < 36; i++)
        for (j = i + 1; j < 36; j++)
            for (k = j + 1; k < 36; k++)
            {
                if (isTriangle(map[i], map[j], map[k]))
                {
                    count++;
                    cout << map[i] << " " << map[j] << " " << map[k] << endl;;
                }
            }
    return count;
}

上述函数中，直接三重for语句循环，函数isTriangle负责判断三条边是否能组成三角形。设置变量count记录总个数，下面是isTriangle函数的实现：

int isTriangle(char * str1, char * str2, char * str3)
{
    char p1, p2, p3;
    p1 = getCrossPoint(str1, str2);
    if (p1 == NO_POINT) return 0;
    p2 = getCrossPoint(str2, str3);
    if (p2 == NO_POINT) return 0;
    p3 = getCrossPoint(str1, str3);
    if (p3 == NO_POINT) return 0;

    if (p1 != p2 && p2 != p3 && p1 != p3 && isAline(p1, p2, p3) == 0)
    {
        //cout << p1 << " " << p2 << " " << p3 << " ";
        return 1;
    }
    return 0;
}

该函数参数是三个字符指针，getCrossPoint函数的功能是计算两条线段的线端的交点，并将此交点的字母返回。如果str1，str2，str3能构成三角形，那么任意两端线段必然存在交点。对于处于同一条直线上的线段，虽然存在交点，但不能构成三角形，如下图所示：

基于以上三种情况，在获取两两线段的交点后做如下判断：

 if (p1 != p2 && p2 != p3 && p1 != p3 && isAline(p1, p2, p3) == 0)

该语句首先判断两两相交是否不存在重复的点，之后通过函数isAline判断三个点是否处于同一条线。

函数getCrossPoint实现如下：

char getCrossPoint(char * s1, char * s2)
{
    if (*s1 == *s2) return *s1;
    if (*s1 == *(s2 + 1)) return *s1;
    if (*(s1 + 1) == *s2) return *s2;
    if (*(s1 + 1) == *(s2 + 1)) return *(s1 + 1);
    return NO_POINT;
}

函数isAline实现如下：

int isAline(char a, char b, char c)
{
    for (int i = 0; i < 7; i++)
        if (contains(line[i], a) == 1 && contains(line[i], b) == 1 && contains(line[i], c) == 1)
            return 1;
    return 0;
}

判断三个交点是否在一条直线上的步骤是，首先观察原图，找出所有三点处于一线的实例，一字符串数组的保存：

char * line[] = { "adb","agc","aejh","afki","defg","bjkg","bhic" };

将任意线段两两之间的交点拼接在一起，然后判断是否该字符串属于上述中字符串成员或某个成员的子串。contains函数如下：

int contains(char * str, char a)
{
    int i = 0;
    while (str[i] != '\0')
    {
        if (str[i] == a)
            return 1;
        i++;
    }
    return 0;
}

测试主函数：

int main()
{
    int x = printTriangleNumber();
    cout  << "共有 : " << x  << "个三角形"<< endl;
}

12. 递归查找数组中的最大值

int getMaxVal(int * k, int n)
{
    int tmp;
    if (1 == n)
        return k[0];
    else
        tmp = getMaxVal(k + 1, n - 1);
    if (k[0] > tmp)
        return k[0];
    else
        return tmp;
}

13. 分解质因子

任何一个合数都可以分解成几个质数相乘的形式，这几个质数叫做这个合数的质因数。例如 24 = 2 * 2 * 2 * 3.把一个合数写成几个质数相乘的形式叫做分解质因数。对于一个质数它的质数因子可定义为它本身。

质数就是除了1和本身外在没有其他因数的数字。例如3，5，7等；合数就是除了1和本身因数外还有其他因数，例如24除了1和本身外还有2等因数；任何一个合数都可以分解成几个质因数相乘的形。

对一个质数进行质数分解时直接返回该质数即可。如果对一个合数进行质数分解，则从2到n-1顺序的查找n的质数。

int isPrime(int n)
{
    if (n == 1)
        return 1;
    for (int i = 2; i <= n - 1; i++)
        if (n % i == 0)
            return 0;
    return 1;
}

void primeFactor(int n)
{
    if (isPrime(n))
        cout << n << endl;
    else
    {
        for (int i = 2; i <= n - 1; i++)
            if (n % i == 0)
            {
                cout << " " << i << " ";
                primeFactor(n / i);
                break;
            }
    }
}

14. 上楼梯问题

已知楼梯有20阶台阶，上楼梯可以一步上一阶，也可以一步上二阶,也可以一步上三阶。编写程序计算公有多少中不同的上楼方法。

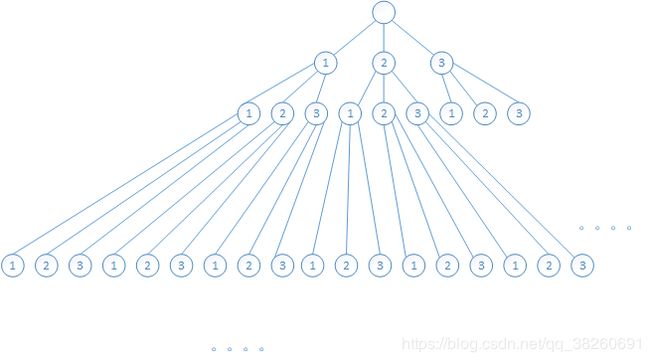
用一棵树描述出所有的解空间：

su所有的方案都包含这个解空间中，其中标号为1的结点表示“一步上1阶”，标号2和3表示一步上两阶和三阶。在搜素解空间树时，从根结点出发，逐层向下搜素。每经过一个结点就将结点中数字 累加，表示已登上的台阶数，当这个数等于20时，就表示找到了一中方案，该结点的下层结点就不必再访问，而是向其父结点回溯并继续搜索下一分支以寻求另外的方案。当累加结果大于20时，表示本条路径不是答案，搜索停止并回溯。

在用代码实现时，通过递归回溯的方法模拟对抽象的解空间树的搜索。

#define MAX_STEPS 20
int _count = 0;
void upStairs(int foot_step, int haveUpStairsCount)
{
    if (haveUpStairsCount + foot_step == MAX_STEPS)
    {
        _count++;
        return;
    }
    if (haveUpStairsCount + foot_step > MAX_STEPS)
        return;
    haveUpStairsCount += foot_step;
    upStairs(1, haveUpStairsCount);
    upStairs(2, haveUpStairsCount);
    upStairs(3, haveUpStairsCount);
}
void upStairsAll()
{
    upStairs(1, 0);
    upStairs(2, 0);
    upStairs(3, 0);
}

测试主函数：

int main()
{
    upStairsAll();
    cout << _count << endl;
}

函数upStairs的功能是统计所有方案数量，使用全局变量_count，避免递归中参数的传递。函数upStairs包含两个参数：foot_step表示每一次递归要累加的步数，对应解空间树结点的值(1,2,3),haveUpStairsCount表示目前为止已走过的步数，每次递归中要将foot_step累加到haveUpStairsCount上，以判断是否超过20阶。

函数upStairs中首先判断haveUpStairsCount + foot_step是否等于MAX_STEPS，如果相等，则count计算加1.然后判断haveUpStairsCount + foot_step是否大于MAX_STEPS，如果大于表示本次递归的路径不满足，直接结束当前递归。

函数upStairsAll将upStairs封装，其中upStairs(1, 0);upStairs(2, 0);upStairs(3, 0);表示第一步对解空间树进行搜索时共有三种选择。

15.  矩阵中的相邻数

编写程序，计算出如下矩阵中第二行第一列元素5相邻的有几个5，所谓相邻是指该元素的上下左右四个方向上的元素，同时相邻的相邻也算相邻元素。

就上面矩阵而言，与第二行第一列的5相邻的共有7个，出去左下角和右下角的5.

解法步骤：

1）定义全局变量count计算共有多少个相邻的5.

2）从第二行第一列的元素出发，依次查找其相邻的4个元素（上下左右），看其中是否有元素5.如果有则count加一，然后将这个5作为新的起点，继续递归搜索。如果相邻元素没有5则执行第三步。

3）返回上一层。

但上述递归思路有两个需要考虑的重要问题：重复搜索和矩阵越界。

所谓重复搜索，是指已经被访问过的元素再一次被访问。例如在访问上述矩阵中第二行第二列元素时，它的左边的元素5已经被访问过，在递归中应避免重复搜索。

为了避免重复搜索，程序中设置了一个同等规模的矩阵q，其初始化所有元素为0，程序一旦访问到某个5就将其对应位置上的0变为1。每次查找元素时都要查看矩阵q，只有q中对应位置为0时，才能统计相邻元素5并以此为起点。否则说明该位置已经被统计过了。

关于矩阵越界问题。有时某些元素并没有完整的上下左右4个相邻的元素。例如第一列的元素就每有左边的元素，所以在设计程序时要考虑到并不是每一个元素都要查找其上下左右4个元素。

声明全局变量和全局数组：

extern int _count;

extern int p[5][5];
extern int q[5][5];

初始化全局数组和全局变量：

int _count = 0;

int p[5][5] =
{ 1,1,5,5,1,
5,5,5,1,1,
1,1,5,5,1,
1,1,5,1,1,
5,1,1,1,5
};
int q[5][5] = { 0 };

检测下标是否越界以及是否重复访问的子函数:

int isValid(int i, int j)
{
    if (i < 0 || i > 4 || j < 0 || j > 4)
        return 0;
    if (q[i][j] == 1)
        return 0;
    return 1;
}

递归实现的搜查函数：

void adjacentNumber(int i, int j, int k)
{
    q[i][j] = 1;
    if (isValid(i - 1, j))
    {
        if (p[i - 1][j] == k)
        {
            _count++;
            q[i - 1][j] = 1;
            adjacentNumber(i - 1, j, k);
        }
    }
    if (isValid(i + 1, j))
    {
        if (p[i + 1][j] == k)
        {
            _count++;
            q[i+1][j] = 1;
            adjacentNumber(i + 1, j, k);
        }
    }
    if (isValid(i, j - 1))
    {
        if (p[i][j - 1] == k)
        {
            _count++;
            q[i][j -1] = 1;
            adjacentNumber(i, j -1, k);
        }
    }
    if (isValid(i, j + 1))
    {
        if (p[i][j + 1] == k)
        {
            _count++;
            q[i][j + 1] = 1;
            adjacentNumber(i, j + 1, k);
        }
    }
}

函数adjacentNumber包含3个参数：参数i和j表示查找矩阵中位置，也是递归搜索的起点。参数k表示搜索元素的值也就是5.

测试主函数：

int main()
{
    adjacentNumber(1, 0, 5);
    for (int i = 0; i < 5; i++)
    {
        for (int j = 0; j < 5;j++)
            cout << p[i][j] << " ";
        cout << endl;
    }
    cout << endl;

    for (int i = 0; i < 5; i++)
    {
        for (int j = 0; j < 5;j++)
            cout << q[i][j] << " ";
        cout << endl;
    }
    cout << endl;

    cout << "共有 :"<<_count  << "个"<< endl;
}

adjacentNumber(1, 0, 5);表示按题目要求从第二行第一列的元素5开始搜索。

测试结果：

1 1 5 5 1
5 5 5 1 1
1 1 5 5 1
1 1 5 1 1
5 1 1 1 5

0 0 1 1 0
1 1 1 0 0
0 0 1 1 0
0 0 1 0 0
0 0 0 0 0

共有 :7个
请按任意键继续. . .