C/C++线性结构

目录

1. 数组和顺序表

2. 单链表

2.0 C语言方式实现

 2.1 C++方式实现

3. 循环链表

4. 双向链表

5. 队列与栈

5.0 栈C++的实现

5.1 队列的C++实现

---

1. 数组和顺序表

1.0 向顺序表中的第i个位置插入元素。

顺序表定义：

#define MAXSIZE 10
#define INCREMENT 10
typedef struct
{
    int * elem;
    int length;
    int size;
}Seqlist;

创建顺序表：

Seqlist * createList()
{
    Seqlist * l = (Seqlist *)malloc(sizeof(Seqlist));
    l->elem = (int *)malloc(sizeof(int) * MAXSIZE);
    l->length = 0;
    l->size = MAXSIZE;
    return l;
}

 在pos位置插入元素：
int InsertElem(Seqlist * l, int pos, int elem)
{
    if (l == NULL) return 0;
    if (pos < 0 || pos >l->length) return 0;
    if (l->length >= l->size)
    {
        int * new_elem = (int *)realloc(l->elem, sizeof(int) * (l->size + INCREMENT));
        if (new_elem == NULL) return 0;
        l->elem = new_elem;
        l->size = l->size + INCREMENT;
    }
    for (int i = l->length - 1; i >= pos;i--)
    {
        l->elem[i + 1] = l->elem[i];
    }
    l->elem[pos] = elem;
    l->length++;
    return 1;
}

打印函数：

void printList(Seqlist *l)
{
    if (l == NULL) return;
    for (int i = 0;i < l->length;i++)
        cout << l->elem[i] << " " << endl;
    cout << endl;
}

主函数：

int main()
{
    Seqlist * l = createList();
    for (int i = 0; i < 15;i++)
        InsertElem(l, 0, (i + 1));
    printList(l);
}

1.1 实现数组逆置。

void reverseSeqList(int a[], int n)
{
    int temp;
    for (int i = 0; i < (n - 1) / 2;i++)
    {
        temp = a[i];
        a[i] = a[n - 1 - i];
        a[n - 1 - i] = temp;
    }
    for (int i = 0; i < n;i++)
        cout << a[i] << " ";
    cout << endl;
}

int main()
{
    int a[10];
    for (int i = 0; i < 10;i++)
        a[i] = i + 1;
    reverseSeqList(a, 10);
}

1.2 实现删除一个数组中的重复元素。

编写一个函数，删除一个只包含正整数的数组中重复元素，例如，一个数组中元素为{2，3，5，2，5，3，6，9，11，6}，删除重复元素后数组变为{2，3，5，6，9，11}。

void delElem(int a[], int * n)
{
    int i = 0, j;
    while (i < *n)
    {
        j = i + 1;
        while (j < *n)
        {
            if (a[i] == a[j])
            {
                for (j = j + 1;j < *n; j++)
                    a[j-1] = a[j];
                *n = *n - 1;
            }
            else
                j++;
        }
        i++;
    }
}

int main()
{
    int a[10] = { 2,3,5,5,9,4,3,7,4,2 };
    int n = 10;
    delElem(a, &n);
    for (int i = 0;i < n;i++)
        cout << a[i] << " ";
    cout << endl;
}

1.3 求数组元素两两之间的差绝对值的最小值。

要求得出最小值即可，不要求得出是那两个数。

int findMin(int a[], int n)
{
    int min_val = abs(a[0] - a[1]);
    for (int i = 0; i < n;i++)
    {
        for (int j = i + 1;j < n;j++)
        {
            if (abs(a[i] - a[j]) < min_val)
                min_val = abs(a[i] - a[j]);
        }
    }
    return min_val;
}

int main()
{
    int a[5] = { 1,3,5,8,9 };
    int x = findMin(a, 5);
    cout << x << " " << endl;
}

1.4 两个有序数组的交集。

给定两个有序数组arr_1和arr_2，数组中的元素是递增的，且个数组中没有重复的元素。计算两个数组的交集。例如，array_1 = {2,5,6,8,9},array_2 = {1,5,6,7,8}，他们的交集为{5,6,8}

int getIntersection(int arr_1[], int len_1, int arr_2[], int len_2,int intersection[])
{
    int i = 0, j = 0, k = 0;
    while (i < len_1  && j < len_2)
    {
        if (arr_1[i] > arr_2[j])
            j++;
        if (arr_1[i] < arr_2[j])
            i++;
        if (arr_1[i] == arr_2[j])
        {
            intersection[k] = arr_1[i];
            i++;
            j++;
            k++;
        }
    }
    return k;
}

上述算法中参考数组的二路归并法。用变量i指向array_1的第一个元素，变量 j 指向array_2的第一个元素。执行下面的操作：

1）如果array_1[i]等于array_2[j],则该元素是交集元素，将其放到intersection数组中，然后执行i++，j++，。

2) 如果array_1[i]大于array_2[j]，则执行j++。

3）如果array_[1]小于array_2[j]，则执行i++。

4）一旦 i 等于数组array_1的长度，或者j 等于array_2的长度，循环终止。

1.5 判断数组中的元素是否连续。

现有一个整型数组，其元素0~65535之间的任意数字，已知相同的数字不会重复出现，而0可以重复出现，且0可以通配成任意一个数字，设计算法判断该数组中元素是否连续。

有一个很巧妙的解决方法。如果一个数组包含n个元素，并且该数组中元素是连续的，那么它一定具有“数组中最大值与最小值之差为 n - 1”的性质。如果这些元素中包含0这样的通配数字，并且要保证数组中元素是连续的，那么数组中的非0最大值与非0最小值之差不能超过n - 1.

例如，数组中元素为{5，7，6，0，9，10}，该数组包含6个元素，非0元素最大值为10，非0元素最小值为5，两者之差等于5，即等于n-1 ，即6 -1，所以该数组是连续的。

例如，数组{2，3，7，0，0}，非0最大值是7，非0最小值是2，7-2 = 5 > n - 1 = 4。所以数组不是连续的。

int isContinuousArray(int array[], int len)
{
    int max_val = array[0], min_val = array[0];
    for (int i = 1; i < len; i++)
    {
        if (array[i] > max_val && array[i] != 0)
            max_val = array[i];
        else  if (array[i] < min_val && array[i] != 0)
            min_val = array[0];
    }
    if (max_val - min_val > len - 1)
        return 0;
    else
        return 1;
}
int main()
{
    int arr_1[6] = { 5,7,6,0,9,10 };
    int arr_2[5] = { 2,3,7,0,0 };
    int ret = isContinuousArray(arr_2, 5);
    if (ret)
        cout << "Is continus!" << endl;
    else
        cout << "Not continus!" << endl;
} 

1.6 判断数组中是否有重复元素。

给定一个长度为N的数组，其中每个元素的取值范围都是1~N。判断数组中是否有重复的数字。

由于原数组长度为N，并且取值范围是1~N，如果数组中不包含重复元素，那么数组中元素一定是1~N内每个都出现一次，这N个数的和是N * (N + 1) / 2。所以所有元素之和不等于N * (N + 1) / 2，那么数组一定包含重复元素。

int haveRepeatElem(int arr[], int n)
{
    int sum = 0;
    for (int i = 0; i < n; i++)
        sum += arr[i];
    if (sum != (n * (n + 1) / 2))
        return 1;
    else
        return 0;
}

int main()
{
    int arr_1[6] = { 1,3,2,5,4,6 };
    int ret = haveRepeatElem(arr_1, 6);
    if (ret)
        cout << "have repeat!" << endl;
    else
        cout << "not repeat!" << endl;
}

2. 单链表

2.0 C语言方式实现

LinkList.h文件

#pragma once
#include
using namespace std;

struct Header
{
    int length;
    struct Node * next;
};

struct Node
{
    int data;
    struct Node * next;
};

typedef struct Header Head;
typedef struct Node List;

Head * createList();
int insertList(Head * head,int pos,int val);
int deleteList(Head * head, int val);
List * findList(Head * head, int val);
int destoryList(Head * head);
void printList(Head * head);

Linklist.c文件

Head * createList()
{
    Head * head = (Head *)malloc(sizeof(Head));
    if (head == NULL) return NULL;
    head->length = 0;
    head->next = NULL;
    return head;
}

int insertList(Head * head, int pos, int val)
{
    if (head == NULL || pos < 0 || pos > head->length)
        return 0;
    List * pVal = (List *)malloc(sizeof(List));
    pVal->data = val;

    List * pCur = head->next;
    if (pos == 0)
    {
        head->next = pVal;
        pVal->next = pCur;
    }
    else
    {
        for (int i = 1; i < pos; i++)
            pCur = pCur->next;
        pVal->next = pCur->next;
        pCur->next = pVal;
    }
    head->length++;
    return 1;
}

int deleteList(Head * head, int val)
{
    if (head == NULL) return 0;

    List * pCur = head->next;
    List * pTmp = NULL;

    if (pCur->data == val)
    {
        head->next = pCur->next;
        free(pCur);
        head->length--;
        return 1;
    }
    else
    {
        for (int i = 1; i < head->length;i++)
        {
            pTmp = pCur;
            pCur = pCur->next;
            if (pCur->data == val)
            {
                pTmp->next = pCur->next;
                free(pCur);
                head->length--;
                return 1;
            }
        }
    }
}

List * findList(Head * head, int val)
{
    if (head == NULL) return NULL;

    List * pCur = head->next;
    for (int i = 0; i < head->length;i++)
    {
        if (pCur->data == val)
            return pCur;
        else
            pCur = pCur->next;
    }
}

int destoryList(Head * head)
{
    if (head == NULL) return 0;

    List * pCur = head->next;
    List * pTmp = NULL;
    while (pCur != NULL)
    {
        pTmp = pCur;
        pCur = pCur->next;
        free(pTmp);
    }
    head->length = 0;
    head->next = NULL;
}

void printList(Head * head)
{
    if (head == NULL) return;
    List * pCur = head->next;
    while (pCur != NULL)
    {
        cout << pCur->data << " ";
        pCur = pCur->next;
    }
    cout << endl;
}

测试主函数

int main()
{
    Head * head = createList();
    for (int i = 0;i < 10; i++)
    {
        insertList(head,0,(i + 1));
    }
    cout << "插入10个数字后遍历 ：\n";
    printList(head);
    cout << "删除元素值为7的结点后遍历 ：\n";
    deleteList(head, 7);
    printList(head);
    cout << "查找值为5的结点并输出其值：\n";
    List * p = findList(head, 5);
    cout << p->data << " " << endl;
    cout << "销毁\n";
    destoryList(head);
}

2.0.0 合并两个单链表。

void mergeList(Head * list1, Head * list2)
{
    if (list1 == NULL || list2 == NULL) return;
    List * pCur = list1->next;
    while (pCur->next != NULL)    //定位到list1的最后一个结点
        pCur = pCur->next;

    pCur->next = list2->next;            
    list1->length += list2->length;

}

int main()
{
    Head * list1 = createList();
    for (int i = 0;i < 5; i++)
    {
        insertList(list1,0,(i + 1));
    }
    printList(list1);

    Head * list2 = createList();
    for (int i = 0;i < 5; i++)
    {
        insertList(list2, 0, (i + 5));
    }
    printList(list2);

    mergeList(list1, list2);

    printList(list1);
}

 2.0.1 单链表的逆置

void reverseList(Head * list)
{
    if (list == NULL) return;
    List * pCur = list->next;
    List * q = NULL;
    List * r = NULL;
    while (pCur != NULL)
    {
        r = q;
        q = pCur;
        pCur = pCur->next;
        q->next = r;
    }
    list->next = q;
} 

int main()
{
    Head * list1 = createList();
    for (int i = 0;i < 5; i++)
    {
        insertList(list1,0,(i + 1));
    }
    printList(list1);

    reverseList(list1);

    printList(list1);
}

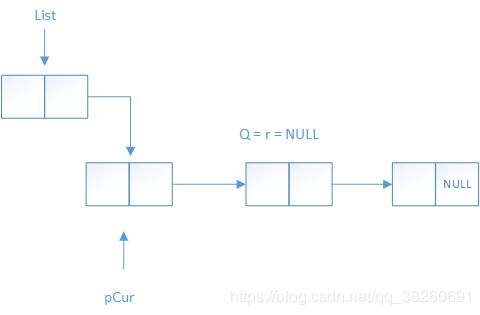
上述算法中， 初始状态下，即while循环未开始前的链表如下所示：

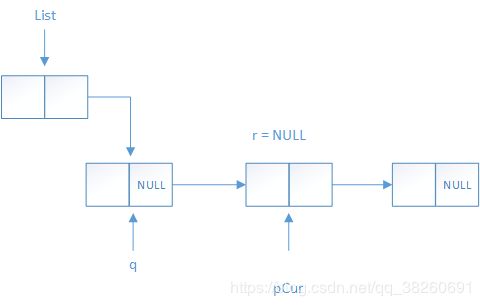
 第一次循环后，指针r = NULL，指针q指向源链表的第一个结点，指针pCur指向原链表的第二个结点，将指针q的next域回指r，也即将源链表的第一个结点的next置NULL.此时示意图如下：

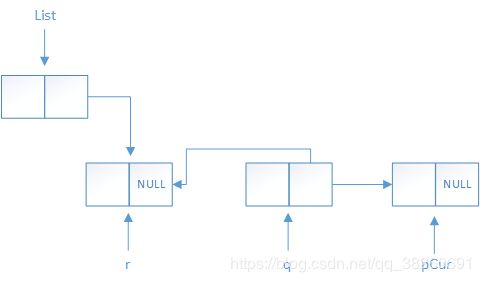
第二次循环后，由于while循环中第一句将q赋值给r，也就是说第二次循环中，指针r指向le源链表的第一个结点。

此时，指针pCur指向第三个结点，指针q指向第二个结点。将q的next域指向r也即指向第一个结点。此时示意图如下：

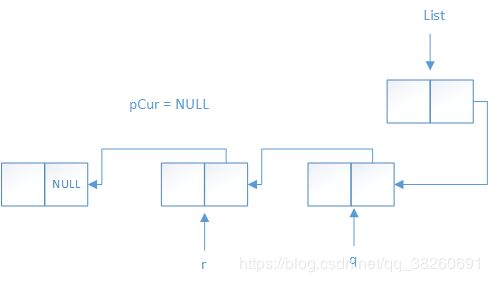
 循环结束后，指针pCur指向NULL，指针q指向原链表的最后一个结点，指针r指向原连表倒数第二个结点，此时，还需要最后一步操作，将头结点指向原链表的最后一个结点，即可实现单链表的逆置。

2.0.2 找出单链表倒数第K个元素

由于实现中采用了带头结点的形式，所以已知了链表的长度，倒数第K个结点的正数位序为length-K，只需要在for循环中找出该结点即可。

List * findK(Head * list, int k)
{
    if (list == NULL) return NULL;
    if (k < 0 || k > list->length) return NULL;

    List * pCur = list->next;
    for (int i = 0; i < list->length - k; i++)
        pCur = pCur->next;
    return pCur;
}

 2.1 C++方式实现

template
class LinkList
{
private:
    struct Node
    {
        T data;
        Node * next;
    };
    int _length;
    Node * _head;
public:
    LinkList();
    ~LinkList();

    void Insert(int pos, const T &val);
    void Remove(int pos);
    int Search(const T &val) const;
    T Visit(int pos) const;

    void Print() const;
    int size() const { return _length; }
    bool Empty() const { return _length == 0; }
};

template
LinkList::LinkList() : _length(0)
{
    _head = new Node;
    _head->next = NULL;
}

template
LinkList::~LinkList()
{
    if (!Empty())
    {
        Node * pCur = _head->next;
        Node * pTmp = NULL;
        while (pCur != NULL)
        {
            pTmp = pCur;
            pCur = pCur->next;
            delete pTmp;
        }
        delete _head;
        _head = NULL;
        _length = 0;
    }
}

template
void LinkList::Insert(int pos, const T &val)
{
    if (pos < 0 || pos > _length) return;

    Node * pVal = new Node;
    pVal->data = val;
    pVal->next = NULL;

    Node * pCur = _head->next;
    if (pos == 0)
    {
        _head->next = pVal;
        pVal->next = pCur;
        _length++;
        return;
    }
    else
    {
        for (int i = 1; i < pos; i++)
            pCur = pCur->next;
        pVal->next = pCur->next;
        pCur->next = pVal;
        _length++;
        return;
    }
}

template
void LinkList::Remove(int pos)
{
    if (Empty()) return;
    if (pos < 0 || pos > _length) return;

    Node * pCur = _head->next;
    if (pos == 0)
    {
        _head->next = pCur->next;
        delete pCur;
        _length--;
    }
    else
    {
        Node * pTmp = NULL;
        for (int i = 1; i < pos; i++)
            pCur = pCur->next;
        pTmp = pCur->next;
        pCur->next = pTmp->next;
        delete pTmp;
        _length--;
    }
}

template
int LinkList::Search(const T &val) const
{
    if (Empty()) return 65535;
    Node * pCur = _head->next;
    int count = 0;
    while (pCur != NULL)
    {
        if (pCur->data == val)
            return count;
        else
        {
            count++;
            pCur = pCur->next;
        }
    }
    return 65535;
}

template
T LinkList::Visit(int pos) const
{
    if (Empty()) return static_cast(65535);
    if (pos <0 || pos > _length) return static_cast(65535);
    
    Node * pCur = _head->next;
    if (pos == 0)
    {
        return pCur->data;
    }
    else
    {
        for (int i = 1;i < pos; i++)
            pCur = pCur->next;
        return pCur->next->data;
    }
}

template
void LinkList::Print() const
{
    if (Empty()) return;
    Node * pCur = _head->next;
    while (pCur != NULL)
    {
        cout << pCur->data << " ";
        pCur = pCur->next;
    }
    cout << endl;
}

3. 循环链表

循环链表最后一个结点的指针域指向第一个结点。

3.0 判断一个列表是否构成循环。

此处指的循环，并非单指链表最后一个结点指向第一个结点，而是更广泛的指链表中任意两个或更多结点构成回环的情况，比如，在单链表中最后一个结点指向了倒数第二个结点，亦可称之为循环。

在带头结点的单链表中，因为已知长度，即结点个数信息，则比较好处理。遍历该链表，并记下结点个数，倘若记下的结点个数大于了链表长度，而还未遍历完单链表，则该链表是循环链表。

如果在不带头结点的单链表中，有一个更直接的办法：初始条件下，设置两个指针slow和fast，slow指向链表的第一个结点，fast指向第二个结点。然后slow和fast皆顺序遍历链表，在遍历过程中，slow一次只访问一个结点，fast访问两个结点。在slow和fast每完成一次访问后都要判断slow是否等于fast，或者fast是否为NULL。如果fast等于slow说明是循环链表，如果fast等于NULL说明不是循环链表。

理解该算法时，可以形象的想象成两个运动员赛跑，如果赛道是直的那么一定是跑得快的先到终点。如果是无尽头的循环跑到则跑的快的终有和跑的慢的相遇的时候。

int isLoopList(Head * list)
{
    if (list == NULL) return 0;
    Node * pfast = list->next->next;
    Node * pslow = list->next;
    while (1)
    {
        if (pfast == NULL || pfast->next == NULL)
            return 0;
        else if (pfast == pslow || pfast->next == pslow)
            return 1;
        else
        {
            pfast = pfast->next->next;
            pslow = pslow->next;
        }
    }
}

4. 双向链表

下面以C++类封装一个双向链表。

#pragma once
#include
using namespace std;

template
class DList
{
private:
    struct Node
    {
        T data;
        Node * pre;
        Node * next;
    };
    int _length;
    Node * _head;
public:
    DList();
    ~DList();

    void Insert(int pos, const T &val);
    void Remove(int pos);
    int Search(const T &val) const;
    T Visit(int pos) const;

    void Print() const;
    int Size() const { return _length; }
    bool Empty() const { return _length == 0; }
};

template
DList::DList() : _length(0)
{
    _head = new Node;
    _head->pre = _head->next = NULL;
}

template
inline DList::~DList()
{
    if (!Empty())
    {
        Node * pCur = _head->next;
        Node * pTmp;
        while (pCur != NULL)
        {
            pTmp = pCur->next;
            delete pCur;
            pCur = pTmp;
        }
        _length = 0;
    }
    delete _head;
}

template
void DList::Insert(int pos, const T &val)
{
    if (pos < 0 || pos > _length) return;
    Node * pVal = new Node;
    pVal->data = val;
    pVal->pre = pVal->next = NULL;
    
    Node * pCur = _head->next;
    if (Empty())
    {
        _head->next = pVal;
    }
    else
    {
        if (pos == 0)
        {
            _head->next = pVal;
            pVal->pre = NULL;
            pVal->next = pCur;
            pCur->pre = pVal;
        }
        else
        {
            for (int i = 1; i < pos; i++)
                pCur = pCur->next;
            pVal->next = pCur->next;
            pCur->next->pre = pVal;
            pVal->pre = pCur;
            pCur->next = pVal;
        }
    }
    _length++;
}

template
void DList::Remove(int pos)
{
    if (pos < 0 || pos >_length || Empty()) return;
    Node * pCur = _head->next;
    if (pos == 0)
    {
        _head->next = pCur->next;
        pCur->next->pre = NULL;
        delete pCur;
    }
    else
    {
        for (int i = 1; i < pos; i++)
            pCur = pCur->next;
        Node * pTmp = pCur->next;
        pTmp->next->pre = pCur;
        pCur->next = pTmp->next;
        delete pTmp;
    }
    _length--;
}

template
int DList::Search(const T &val) const
{
    if (Empty()) return 65535;
    Node * pCur = _head->next;
    int count = 0;
    while (pCur != NULL)
    {
        if (pCur->data == val)
            return count;
        else
        {
            pCur = pCur->next;
            count++;
        }
    }
    return 65535;
}

template
T DList::Visit(int pos) const
{
    if (pos < 0 || pos > _length || Empty()) return static_cast(65535);
    Node * pCur = _head->next;
    for (int i = 0; i < pos; i++)
        pCur = pCur->next;
    return pCur->data;
}

template
void DList::Print() const
{
    if (Empty()) return;
    Node * pCur = _head->next;
    while (pCur != NULL)
    {
        cout << pCur->data << " ";
        pCur = pCur->next;
    }
    cout << endl;
}

主函数

int main()
{
    DList dlist;
    for (int i = 0; i < 10; i++)
        dlist.Insert(0, i + 1);
    dlist.Print();

    int ret = dlist.Search(7);
    cout << ret << endl;

    ret = dlist.Visit(ret);
    cout << ret << endl;

    dlist.Remove(3);
    dlist.Print();
}

5. 队列与栈

5.0 栈C++的实现

#pragma once
#include
using namespace std;
template
class LinkStack
{
private:
    struct Node
    {
        T data;
        Node * next;
    };
    Node * _top;
    int _size;
public:
    LinkStack();
    ~LinkStack();

    void Push(const T &val);
    T Pop();
    T Top();
    bool Empty() const { return _size == 0; }
    int Size() const { return _size; }
 };

template
LinkStack::LinkStack() : _size(0)
{
    _top = NULL;
}

template
LinkStack::~LinkStack()
{
    if (!Empty())
    {
        Node * pCur = _top;
        Node * p;
        while (pCur != NULL)
        {
            p = pCur->next;
            delete pCur;
            pCur = p;
        }
        _size = 0;
    }
}

template
void LinkStack::Push(const T &val)
{
    Node * pVal = new Node;
    pVal->data = val;
    pVal->next = _top;
    _top = pVal;
    _size++;
}

template
T LinkStack::Pop()
{
    if (Empty()) return static_cast(65535);
    Node * pCur = _top;
    _top = _top->next;
    T val = pCur->data;
    delete pCur;
    _size--;
    return val;
}

template
T LinkStack::Top()
{
    if (Empty()) return 65535;
    return _top->data;
}

测试主函数：

int main()
{
    LinkStack stack;
    srand(time(NULL));
    cout << "入栈 : \n";
    for (int i = 0; i < 10;i++)
    {
        int ret = rand() % 100 + 1;
        cout << ret << " ";
        stack.Push(ret);
    }
    cout << endl;
    cout << "出栈 : \n";
    for (int i = 0; i < 10;i++)
    {
        cout << stack.Pop() << " ";
    }
    cout << endl;
}

5.0.1  十进制数转换为其他进制数

char * Convert(int num,int r)
{
    LinkStack stack;
    while (num != 0)
    {
        stack.Push(num % r);
        num = num / r;
    }
    char * buf = (char *)malloc(sizeof(char) * (stack.Size() + 1));
    int i = 0;
    while (!stack.Empty())
    {
        int ret = stack.Pop();
        if (ret > 9) buf[i] = char(ret + 'A' - 10);
        else buf[i] = char(ret + 0x30);
        i++;
    }
    buf[i] = '\0';
    return buf;
}
int main()
{
    char * buf = Convert(1000, 16);
    cout << buf << endl;

}

 5.0.2  括号匹配问题

已知表达式中只允许两种括号：圆括号（）和方括号[ ] 。它们可以任意嵌套使用。要求括号必须成对出现。编写一个函数，从终端输入一组括号，以字符#结束，判断输入的括号是否匹配合法。

int Match(char ch1, char ch2)
{
    if (ch2 == '(' && ch1 == ')') return 1;
    if (ch2 == '[' && ch1 == ']') return 1;
    return 0;
}
void matchBracket()
{
    LinkStack s;
    char ch1, ch2;
    scanf("%c", &ch1);
    while(ch1 != '#')
    {
        if (s.Empty())
            s.Push(ch1);
        else
        {
            ch2 = s.Pop();
            if (Match(ch1, ch2) != 1)
            {
                s.Push(ch2);
                s.Push(ch1);
            }
        }
        scanf("%c", &ch1);
    }
    if (s.Empty())
        cout << "完全匹配\n";
    else
        cout << "匹配错误\n";
}

int main()
{
    matchBracket();
}

  5.0.2  用两个栈实现一个队列

用C++实现如下

方法：入队操作时，将元素压入栈s1中；出队操作时判断s2是否为空，如果s2不为空，则直接取出s2的栈顶元素；如果s2为空，则将s1的元素逐个弹出并压入s2，再取s2的栈顶元素。函数emptyQueue通过判断栈s1和s2是否都为空来实现。函数getCount通过计算s1和s2的当前容量之和来实现。

template
class SQueue
{
private:
    LinkStack _s1, _s2;
public:
    void enQueue(const T &x);
    T deQueue();
    bool emptyQueue();
    int getCount();
};

template
void SQueue::enQueue(const T & x)
{
    _s1.Push(x);
}

template
T SQueue::deQueue()
{
    if (_s2.Empty())
    {
        if (_s1.Empty())
            return T(0);
        else
        {
            while (!_s1.Empty())
                _s2.Push(_s1.Pop());
        }
    }
    T x = _s2.Pop();
    return x;
}

template
bool SQueue::emptyQueue()
{
    if (_s1.Empty() && _s2.Empty())
        return true;
    else return false;
}

template
int SQueue::getCount()
{
    return _s1.Size() + _s2.Size();
}

测试主函数

int main()
{
    SQueue sq;
    for (int i = 0; i < 10; i++)
        sq.enQueue(i + 1);
    int ret;
    ret = sq.getCount();
    cout << ret << endl;
    for (int i = 0; i < 10; i++)
    {
        cout << sq.deQueue() << " ";
    }
    cout << endl;
}

5.1 队列的C++实现

 

#pragma once
#include
using namespace std;

template
class LinkQueue
{
private:
    struct Node
    {
        T data;
        Node * next;
    };
    Node * _front;
    Node * _rear;
public:
    LinkQueue() { _front = _rear = NULL; }
    ~LinkQueue() { Clear(); }

    void Clear();
    void enQueue(const T &val);
    T deQueue();
    T getHead() const;
    bool Empty() const { return _front == NULL; }
    int getSize() const;
};

template
inline void LinkQueue::Clear()
{
    Node * pCur = _front;
    Node * p;
    while (pCur != NULL)
    {
        p = pCur->next;
        delete pCur;
        pCur = p;
    }
}

template
inline void LinkQueue::enQueue(const T & val)
{
    Node * pVal = new Node;
    pVal->data = val;
    pVal->next = NULL;
    if (_front == NULL)
        _front = _rear = pVal;
    else
    {
        _rear->next = pVal;
        _rear = pVal;
    }
}

template
inline T LinkQueue::deQueue()
{
    if (Empty()) return T(65535);
    Node * pCur = _front;
    _front = _front->next;
    T val = pCur->data;
    if (_front == NULL)
        _rear = NULL;
    delete pCur;
    return val;
}

template
inline T LinkQueue::getHead() const
{
    if (Empty()) return T(65535);
    return _front->data;
}

template
inline int LinkQueue::getSize() const
{
    if (Empty()) return 0;
    Node * pCur = _front;
    int count = 0;
    while (pCur != NULL)
    {
        count++;
        pCur = pCur->next;
    }
    return count;
}

测试主函数

int main()
{
    LinkQueue lq;
    for (int i = 0; i < 10; i++)
        lq.enQueue(i + 1);
    for (int i = 0;i < 10; i++)
    {
        cout << lq.deQueue() << " ";
    }
    cout << endl;
}