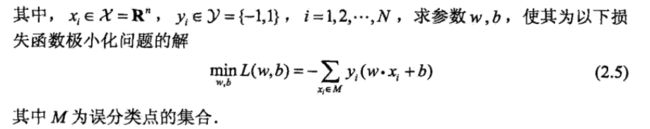【李航统计学习方法】感知机模型

目录

一、感知机模型

二、感知机的学习策略 

三、感知机学习算法 

感知机算法的原始形式

感知机模型的对偶形式 

参考文献

---

本章节根据统计学习方法，分为模型、策略、算法三个方面来介绍感知机模型。 首先介绍感知机模型，接着介绍感知机的学习策略，也就是最小化损失函数，最后介绍感知机学习的算法，分为原始形式和对偶形式（当中也介绍了算法的收敛性）【PS:算法也就是随机梯度下降算法】

一、感知机模型

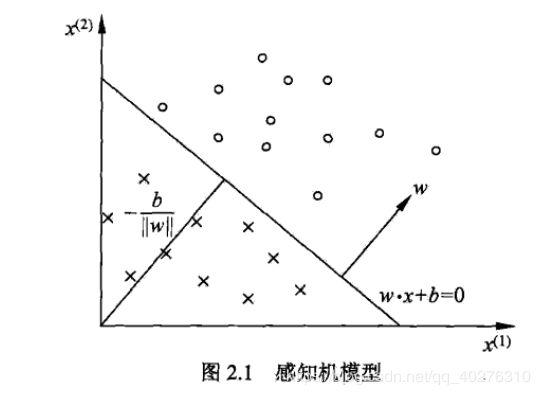
首先感知机（perceptron）模型是一个二类分类的线性分类模型，属于判别模型。其输入为实例的特征向量，输出 为实例的类别，取+1和–1二值。我是不喜欢看定义，倒不如用几何模型来的直观。

以上就是感知机模型的作用，旨在求出将训练数据进行线性划分分离超平面，为此，导入基于误分类的损失函数，利用梯度下降法对损失函数进行极小化， 求得感知机模型，利用学习得到的感知机模型对新的输入实例进行分类。（做的就是分类的事情，尘归尘土归土！）。但是既然有了几何模型，总得来点数学公式吧，不然怎么写代码进行计算，是吧？

2.1， 2.2  两个数学表达式，麻烦记住，划重点！（滑稽!）

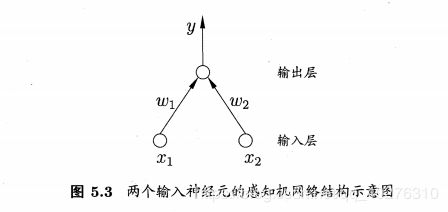
插个广告，你学感知机就是想学神经网络，是不是，来看看西瓜书上的感知机模型吧：

二、感知机的学习策略 

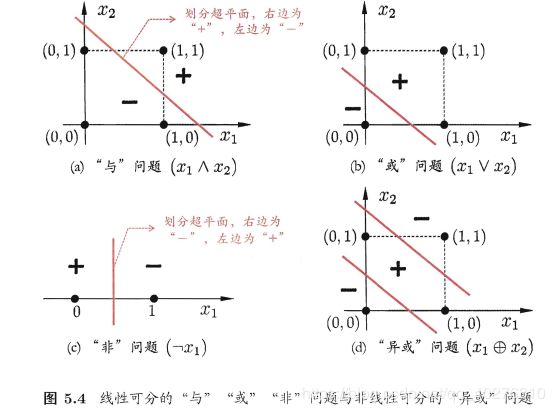
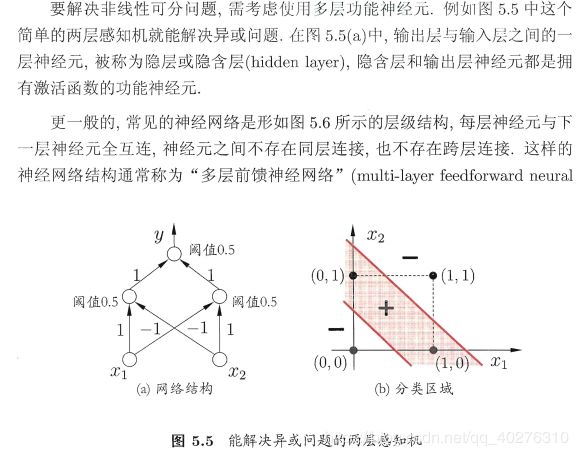
学习策略，通过别人的讲解，一般来说，学习策略就是指的损失函数（咱也不知道这句话对不对，姑且就这样相信吧！）定义2.2首先来了一个数据集的线性可分性，说白了就是说，感知机只能解决线性可分的问题，不能解决非线性可分的问题。（啥？你不懂啥线不线性可分，还想知道为什么不能解决？什么才能解决非线性可分？我不知道！你看看西瓜书的解释吧！）

（什么？看不懂？我也不懂，不看了！next！）  假设训练数据集是线性可分的，感知机学习的目标是求得一个能够将训练集正实例点 和负实例点完全正确分开的分离超平面。为了找出一个超平面（你就认为是找一条线）也即确定感知机模型参数 w,b，需要确定一个学习策略，即定义（经验）损失函数并将损失函数极小化。（通俗说，就是要找到一个方法求得一个最佳的w,b）。

这里对于损失函数选择，我的理解就是使得误分类点到超平面的距离之和最小，如果距离为 0 ，那就说明恭喜你，找到了一个可以完美分类的超平面了。以下给出一个大神的解释。（还看不明白，那就继续next，不要放弃，总有一天会搞明白的！）

---

我们从最初的要求有个f(x)，引申到能只输出1和-1的sign(x)，再到现在的wx+b，看起来越来越简单了，只要能找到最合适的wx+b，就能完成感知机的搭建了。前文说过，让误分类的点距离和最大化来找这个超平面，首先我们要放出单独计算一个点与超平面之间距离的公式，这样才能将所有的点的距离公式求出来对不？

先看wx+b，在二维空间中，我们可以认为它是一条直线，同时因为做过转换，整张图旋转后wx+b是x轴，那么所有点到x轴的距离其实就是wx+b的值对不？当然了，考虑到x轴下方的点，得加上绝对值->|wx+b|，求所有误分类点的距离和，也就是求|wx+b|的总和，让它最小化。很简单啊，把w和b等比例缩小就好啦，比如说w改为0.5w，b改为0.5b，线还是那条线，但是值缩小两倍啦！你还不满意？我可以接着缩！缩到0去！所以啊，我们要加点约束，让整个式子除以w的模长。啥意思？就是w不管怎么样，要除以它的单位长度。如果我w和b等比例缩小，那||w||也会等比例缩小，值一动不动，很稳。没有除以模长之前，|wx+b|叫函数间隔，除模长之后叫几何间隔，几何间隔可以认为是物理意义上的实际长度，管你怎么放大缩小，你物理距离就那样，不可能改个数就变。在机器学习中求距离时，通常是使用几何间隔的，否则无法求出解。

 

然后我们来看看李航老师书上的解释：

至于这里为什么不考虑这个1/w，这个好像涉及一个函数间隔和几何间隔，反正就是考不考虑，都不会影响分类效果，为了简化计算就不考虑了。

最后记住损失函数长啥样就行了：

三、感知机学习算法 

感知机学习算法采用的是随机梯度下降算法，说白了，来看一段官方的解释：

然后我这里就只解释感知机算法的原始形式和对偶形式，至于算法收敛性的证明我就不写，（别问，问就是懒得证明！^_^，好吧，我就是不会，打我啊！） 

感知机算法的原始形式

在这里请允许我偷一个懒，我实在是不可能比原书的内容解释的更好，因为个人看来无论怎么讲，无论谁来讲，自己不动手推一遍，根本就弄不清楚（可能是我自己太笨，B站上的讲解视频看了几遍，别人的博客看了几遍，数学表达式我都认识，就是感觉不像个人，最后自己按李航的书老老实实推一遍，把例题一步步做一遍，豁然开朗^_^，骚年，你还看？赶紧动手推啊！）

所以这里我只摆出算法的解释和算法的具体过程，具体内容大家可以参看原书：

上面我们说过，算法解决的问题就是使得损失函数最小化，求得合适的参数 w，b。这里请大家记住以下的2.5， 2.6，2.7，别问为什么，记住理解就行了，划重点，谢谢！

然后，解决问题的方法就是随机梯度下降法：

（看不懂，我也看不懂，就这样吧！next！） 

Python实现代码如下：

'''
author:SingGuo
datetime:2020年6月30日22:45:16
感知机模型的原始形式
'''

import numpy as np

# 初始化数据
def createData():
    x = np.array([[3, 3], [4, 3], [1, 1]])
    y = [1, 1, -1]
    w = [0, 0]
    b = 0
    # lr = 1 # learning_rate
    return x, y, w, b

# 感知机模型
# def sign(w, b, x):
    # f = np.dot(x, w) + b  # x .w + b
    # return int(f)


# 更新系数w, b
def update(x, y, w, b, i):
    w = w + y[i] * x[i]
    b = b + y[i]
    return w, b


def optimization(x, y, w, b):
    misclassification = False
    while not misclassification:
        count = 0
        for i in range(len(y)):
            # f = sign(w, b, x)
            if y[i] * (np.dot(w, x[i]) + b) <= 0:  # 如果是一个误分类实例点
                print('误分类点为：', x[i], '此时的w和b为：', w, b)
                count += 1
                w, b = update(x, y, w, b, i)
        if count == 0:
            print('最终训练得到的w和b为：', w, b)
            misclassification = True
    return w, b


if __name__ == '__main__':
    x, y, w, b= createData()
    optimization(x=x, y=y, w=w, b=b)

运行结果：

感知机模型的对偶形式 

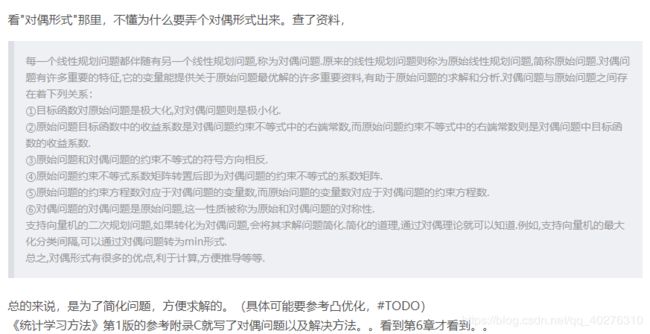
关于对偶形式，我第一反应就是啥叫对偶，在李航老师的书上仅仅只是说：

但是这个意思我懂，就是换种方法解题的意思，在周志华老师的西瓜书中支持向量机这一张对于对偶问题是这样解释的：

（凸二次规划？ 没学过啊！过几天百度看看！拉格朗日？……哎！西瓜书更不懂，于是我找到博客）博客上的解释是这样的：

（假装看的懂的样子，好吧，现在我还是值理解对偶就是换一种更简单的方法简化计算方便求解。至于为啥会有这个形式，可能涉及凸优化的内容，咱也没学，也不会瞎说，那就这样吧！）下面是对偶形式的算法解释：

别问我为啥现在开始贴图了，别问，问就是要睡觉！来吧，直接看代码：

'''
author:SingGuo
datetime:2020年7月1日00:33:39
感知机模型的原始形式
'''

import numpy as np


def creatDataSet():
    group = np.array([[3, 3], [4, 3], [1, 1]])
    label = [1, 1, -1]
    return group, label


def update(x, y, i):
    global a, b, G
    a[i] += 1
    b = b + y


def cal(x, label, row):
    global a, b, G
    result = 0
    for i in range(len(G[row])):
        result += label[i] * a[i] * G[row][i]
    result += b
    result *= label[row]
    return result
    print(result)

def perceptron_func(group, label):
    global a, b, G
    isFind = False
    n = group.shape[0]
    x_col = group.shape[1]
    a = np.zeros(n, dtype=np.int)  # 初始化
    b = 0
    G = np.zeros((n, n), dtype=np.int)

    # 计算Gam矩阵
    for i in range(n):
        for j in range(n):
            G[i][j] = group[i][0] * group[j][0] + group[i][1] * group[j][1]

    while isFind == False:
        for i in range(n):
            if cal(group[i], label, i) <= 0:
                update(group[i], label[i], i)
                print('误分类点为：', group[i], '此时的a1, a2, a3和b为：', a, b)
                break
            elif i == n - 1:
                print('最后迭代的结果为：', a, b)
                isFind = True

if __name__ == '__main__':
    g, l = creatDataSet()
    perceptron_func(g, l)

运行结果为：

这个时候有人问了，为啥两个代码风格不一样？（哎！水平垃圾，对偶形式借鉴别人的，自己写的过程中有一个错误解决不了！我下去慢慢解决） 

（同桌：别找理由，你就是编程太垃圾了！）

（我：……）

参考文献

【1】李航：《统计学习方法》

【2】周志华：《机器学习》

【3】感知机学习算法的对偶形式

【4】感知机对偶问题

【5】感知器、感知器对偶形式（含作业）||《统计学习方法》李航_第1章_蓝皮（学习笔记）

【6】感知机的对偶形式

【7】感知机算法实现（对偶形式）

【8】感知机对偶形式手算过程

【9】统计学习方法(2)——感知机原始形式、对偶形式及Python实现

【10】李航统计学习方法之感知机学习（含感知机原始形式和对偶形式Python代码实现）

【11】李航统计学习方法-感知机python实现

【12】李航统计学习方法-感知机python实现

【13】统计学习方法|感知机原理剖析及实现

 

完结，撒花！！！！！