- 绘本讲师训练营【24期】8/21阅读原创《独生小孩》
1784e22615e0
24016-孟娟《独生小孩》图片发自App今天我想分享一个蛮特别的绘本,讲的是一个特殊的群体,我也是属于这个群体,80后的独生小孩。这是一本中国绘本,作者郭婧,也是一个80厚。全书一百多页,均为铅笔绘制,虽然为黑白色调,但并不显得沉闷。全书没有文字,犹如“默片”,但并不影响读者对该作品的理解,反而显得神秘,梦幻,給读者留下想象的空间。作者在前蝴蝶页这样写到:“我更希望父母和孩子一起分享这本书,使他
- 高级编程--XML+socket练习题
masa010
java开发语言
1.北京华北2114.8万人上海华东2,500万人广州华南1292.68万人成都华西1417万人(1)使用dom4j将信息存入xml中(2)读取信息,并打印控制台(3)添加一个city节点与子节点(4)使用socketTCP协议编写服务端与客户端,客户端输入城市ID,服务器响应相应城市信息(5)使用socketTCP协议编写服务端与客户端,客户端要求用户输入city对象,服务端接收并使用dom4j
- 抖音乐买买怎么加入赚钱?赚钱方法是什么
测评君高省
你会在抖音买东西吗?如果会,那么一定要免费注册一个乐买买,抖音直播间,橱窗,小视频里的小黄车买东西都可以返佣金!省下来都是自己的,分享还可以赚钱乐买买是好省旗下的抖音返佣平台,乐买买分析社交电商的价值,乐买买属于今年难得的副业项目风口机会,2019年错过做好省的搞钱的黄金时期,那么2022年千万别再错过乐买买至于我为何转到高省呢?当然是高省APP佣金更高,模式更好,终端用户不流失。【高省】是一个自
- 每日一题——第八十一题
互联网打工人no1
C语言程序设计每日一练c语言
打印如下图案:#includeintmain(){inti,j;charch='A';for(i=1;i<5;i++,ch++){for(j=0;j<5-i;j++){printf("");//控制空格输出}for(j=1;j<2*i;j++)//条件j<2*i{printf("%c",ch);//控制字符输出}printf("\n");}return0;}
- 2019-12-22-22:30
涓涓1016
今天是冬至,写下我的日更,是因为这两天的学习真的是能量的满满,让我看到了自己,未来另外一种可能性,也让我看到了这两年这几年的过程中我所接受那些痛苦的来源。一切的根源和痛苦都来自于人生,家庭,而你的原生家庭,你的爸爸和妈妈,是因为你这个灵魂在那一刻选择他们作为你的爸爸和妈妈来的,所以你得接受他,你得接纳他,他就是因为他的存在而给你的学习和成长带来这些痛苦,那其实是你必然要经历的这个过程,当你去接纳的
- python os.environ_python os.environ 读取和设置环境变量
weixin_39605414
pythonos.environ
>>>importos>>>os.environ.keys()['LC_NUMERIC','GOPATH','GOROOT','GOBIN','LESSOPEN','SSH_CLIENT','LOGNAME','USER','HOME','LC_PAPER','PATH','DISPLAY','LANG','TERM','SHELL','J2REDIR','LC_MONETARY','QT_QPA
- 今又重阳
芮峻
今又重阳图片发自App白露成霜菊花黄,岁岁重阳,今又重阳。登高远望,君不见,那来时路上少年,青丝已染雪霜。落日一点一点西坠,谁有力量,托住使其回往。转眼缺了大半,又能怎样?江天两茫茫。给我一壶烈酒,我要敬那斜阳,看谁先醉?笑指西天红了一片,借点酒力,老夫聊发一次少年狂。老严.2019年重阳节.杭州
- 2019-08-08
65454
东莞家庭聚会出行旅游去哪里玩住?想起来有很久没有和家里人聚会啦,这次组织家人来到威廉古堡别墅轰趴,一大家子27个人,在别墅订了一天办,玩的非常的开心,小孩子玩游戏机,也很放心不会丢,我们就在唱歌、打麻将、打桌球一系列的活动,还准备小次等小孩生日在别墅举办,还可以给孩子做一个生日的策划
- log4j配置
yy爱yy
#log4j.rootLogger配置的是大于等于当前级别的日志信息的输出#log4j.rootLogger用法:(注意appenderName可以是一个或多个)#log4j.rootLogger=日志级别,appenderName1,appenderName2,....#log4j.appender.appenderName2定义的是日志的输出方式,有两种:一种是命令行输出或者叫控制台输出,另一
- 展现思维导图魅力,不断挖掘人生宝藏
思维导图讲师Mandy
第13期最强思维导图训练营已经结束一周了,但是我依旧是感觉所有学员还在努力的学习,这些学员中有教师、学生、白领、公务员、宝妈等等,只要你努力,只要你想改变自己,任何行业,任何岗位都可以参与进来,28天足以让你见成效,在这28天中,我们的学员不仅仅是收获了一枚毕业证,最重要的是让自己的思维方式得到升级,今天的你为自己投资,明天的你就会感谢你今天的付出,我们来听一听来自13期最强思维导图训练营优秀学员
- Rust基础知识
GRKF15
rust开发语言后端
1.Rust语言简介1.1基础语法变量声明:let关键字用于声明变量,可以指定或不指定类型,如leta=10;和letmutc=30i32;。函数定义:使用fn关键字定义函数,并指定参数类型及返回类型,如fnadd(i:i32,j:i32)->i32{i+j}。控制流:包括if、else等,控制语句后需要使用;来结束语句。1.2数据类型整数类型:i8、i16、i32、i64、i128,以及无符号的
- 2019-3-23晨间日记
红红火火小耳朵
今天是什么日子起床:7点40就寝:23点半天气:有太阳,不过一会儿出来一会儿进去特别清爽的凉意,还蛮舒服的心情:小激动要给女朋友过生日啦纪念日:田田女士过生日任务清单昨日完成的任务,最重要的三件事:1.英语一对一2.运动计划3.认真护肤习惯养成:调整状态周目标·完成进度英语七天打卡(5/7)轻课阅读(87/180)音标课(25/30)读书(福尔摩斯一章)学习·信息·阅读#英语课#Cookingte
- 2019-05-13
王健_100a
【撒下18:2】大卫打发军兵出战,分为三队:一队在约押手下,一队在洗鲁雅的儿子约押兄弟亚比筛手下,一队在迦特人以太手下。大卫对军兵说:“我必与你们一同出战。”解释:大卫检阅部队,将它分成三队,每队由一位元帅统领;约押与兄弟亚比筛,并迦特人以太共同指挥。大卫想与他们一同出战!应用:作为领袖与军兵一起出战是很重要。领袖在事奉中与信徒一起,领袖在任何的环境里与信徒一起走过。我们要同心协力为主而战。祷告:
- 2019-11-04复盘——飞来山上千寻塔,闻说鸡鸣见日升。
那一叶秋
1、大盘篇先上老图,看习惯了,也就知道走势了图1上证指数日线图还是那张老图,自己可以在自己的相关软件上画出来,快变盘了。2、个股篇未加仓、未减仓。分析量能的时候,突然发现这么一个东西:“放量突破年线,缩量回调。”合众科技日线图其实,最近的N只个股,在技术分析上,都到了变盘的临界时候。结合这么久的走势,特别是ZJH不断放开IPO的申请,本质上说是融资难度变大,或者说是为企业的融资开创便利。但现在市场
- 2019-08-16
希望在东方
《春游荣华山》春游荣华山,乍暖还寒。青苔路,石阶险。山路弯上弯!为寻古寺往幽探。细雨已润江南岸,初春芳草现。老树新芽冒枝端,人间又过到新年。今游荣华山,树茂参天,古寺悠闲。细雨飘落发端!三眼井旁,投币许心愿,并祷一世安然。更喜大女明事端,应心安,放开颜。修竹静默,雨中吐心愿。待得春风浩吹时,春笋节节攀。图片发自App图片发自App图片发自App
- 2019-01-19
王小康KK
姓名:王康公司:扬州市方圆建筑工程有限公司2018年3月16日~3月18日上海361期《六项精进》感谢二组学员【日精进打卡第307天】【知~学习】《六项精进》大纲3遍共862遍《大学》通篇3遍共860遍《六项精进》全书40页【经典名句】思想决定行为,行为决定习惯,习惯决定性格,性格决定命运。【行~实践】一、修身:(对自己个人)1、践行六项精进的理念。二、齐家:(对家庭和家人)1、和女朋友视频聊天。
- 2019-10-24
柒月的可可
今日上班无事,人又懒怠动,不知道如何打发这个下午,终于打开了。我大概是把当日记来写的。重庆的天气骤然凉了。早上出门的时候,满地都是落叶,脚踩上去,却是刚下过雨,叶子已润掉,走不出声响。白天在办公室不见天日,对温度也无甚感觉,晚上一个人回到家,屋子里窗户都开着,被冷风吹了一天,一迈进屋,便觉冷气森然。将近二十度的天气,竟要裹着毯子才觉温暖。再过一周,就到十一月。扛过十一月,就可以开暖气了。然而我真的
- 渝婧感恩日记第68天
梁渝婧lydia
1.哇!我真是太幸福啦!感恩奇迹感恩训练营毕业典礼,让我能共振到同学们的喜悦和能量,感谢!感谢!感谢!2.哇!我真是太幸福啦!感恩每天早起,运动3公里!这个星期又做到连续三天,不间断!感谢亲爱的渝婧!你真的是非常的棒!加油,继续坚持!感谢!感谢!感谢!3.哇!我真是太幸福啦!感恩曾正波班主任给我们分享的艾宾浩斯的记忆曲线255学习法,让我蠢蠢欲试,感谢!感谢!感谢!4.哇!我真是太幸福啦!感恩胜利
- 骑昆明到北海—119 砚山县
61清风i
从十年前第一次长途骑行青海湖开始每年一次长途骑行看风景,尝各地美食,探访异域文化,记录途中美食美景美事,已逐渐形成习惯。每年春季详细规划好线路,夏季出行,2020年因为疫情迟迟不能确定线路和行程。总算到了暑期疫情逐渐消失,规划了50多天的云南昆明—广西北海计划。本次行程从云南昆明出发到广西北海市结束,五十一天骑行二千多公里线路昆明-官渡古镇-环滇池--澄江市一抚仙湖—路居镇--江川区--通海县—龙
- 2019考研 | 西交大软件工程
笔者阿蓉
本科背景:某北京211学校电子信息工程互联网开发工作两年录取结果:全日制软件工程学院分数:初试350+复试笔试80+面试85+总排名:100+从五月份开始脱产学习,我主要说一下专业课和复试还有我对非全的一些看法。【数学100+】张宇,张宇,张宇。跟着张宇学习,入门视频刷一遍,真题刷两遍,错题刷三遍。书刷N多遍。从视频开始学习,是最快的学习方法。5-7月份把主要是数学学好,8-9月份开始给自己每个周
- 2019-03-22
430O70Mk
引发支原体的原因支原体感染是临床上比较常见的一种疾病,此疾病会对患者的身体造成很大的伤害,对支原体感染患者的日常生活也会带来极大的影响,那么诱发支原体感染的原因是什么呢?肺炎支原体感染,又称支原体性肺炎,是由肺炎支原体引起的急性间质性肺炎。主要通过呼吸道传播,健康人吸入患者咳嗽,打喷嚏时喷出的口、鼻分泌物而感染。支原体为动物多种疾病的致病体,而其中只有肺炎支原体肯定对人致病。它是由口、鼻分泌物经空
- 今日有感,坚持分享第913天,2019.07.13
ZAF峰回路转
本周是假日里最忙碌的一周,连续四天晚上的课程,让我感觉到身体明显透支。昨天晚上读书会结束回到家,已经是十点半之后啦,忽然感觉身体不舒服,勉强支撑着洗漱完毕,没等上床休息,强烈的不适感警告我该吃药啦!感谢老公半夜到医院給我抓了药,今天早上当我对老公表达谢意的时候,老公说,不用感谢,我不是一直都是这样做的吗?多少年啦,今天竟然还谢谢!老公说的没错,可是以前总感觉那是他应该做的,如今感觉到,身边有一个在
- spring如何整合druid连接池?
惜.己
springspringjunit数据库javaidea后端xml
目录spring整合druid连接池1.新建maven项目2.新建mavenModule3.导入相关依赖4.配置log4j2.xml5.配置druid.xml1)xml中如何引入properties2)下面是配置文件6.准备jdbc.propertiesJDBC配置项解释7.配置druid8.测试spring整合druid连接池1.新建maven项目打开IDE(比如IntelliJIDEA,Ecl
- 每时每刻都是开始2019-03-09
Action熊猫
过去有多少想了无数遍要做的,但实际并没有做到的。以没时间,或其他种种自己认为可以接受的理由,看着一天走啦,一月去啦,又是一年。最后笑一笑,新年不是来了吗!重新开始...如果在过去的365天里,每次醒来,都没能开始,那新年来了,又如何呢?何不把人生的每时每刻都作为起点,不等待,不期盼,不自欺,让每时每刻都在开始中...。
- 2019-03-24
李飞720
姓名:李飞企业名称:临沂鑫道食品有限公司组别373期利他1组日精进打卡第338天】【知~学习】1、阿米巴经营一段2、活用人才1段3、活法、一段【行~实践】一、修身:读书、抽烟减量、俯卧撑个跑步3公里二、齐家、劝说老爸与姑姑和好三、建功、业务洽谈【经典名句分享】1、依据原理原则追求事物的本质,以“作为人,何谓正确”进行判断2、经营者必须为员工物质和精神两方面的幸福殚精竭虑,倾尽全力,必须超脱私心,让
- 2019年8月6日 星期二 晴
李佳晨宝宝
今天我写完作业以后,我玩儿了一会儿我的拼装玩具,拼装玩具是我的世界的游戏里面的乐高,我拿出乐高把它拼成上次的迷宫,然后又给他升级了一下,我拆出上面一些部分的零件加大了游戏的难度,然后我又做了一个小牛圈。这个小牛圈里面住的是猪和牛,还有羊,给那里摆了一块草地,他们想吃东西直接在草地上吃,然后我把牛圈建了一个遮阳伞,防止天气太热把它们晒死。然后这样我的小牛就万无一失了,我再看看加大难度后的迷宫,实在是
- 2019-03-10
Daisy倾夕
生命总是需要一些允许和放纵的释怀,经常熬夜时是对自己有一份责怪,今日却又一份惊喜感!偶尔允许了自己做了一件很久没做的事情会很开心,减肥的时候会因为有一餐对食物欲望内心匮乏的填补而感到开心,偶尔的总是惊喜,长期也容易成为负担,那如何在这个长期的过程中又不失惊喜,我想应该是探索和变化的永恒,允许并好,首先先带上觉知!
- 3286、穿越网格图的安全路径
Lenyiin
题解c++算法leetcode
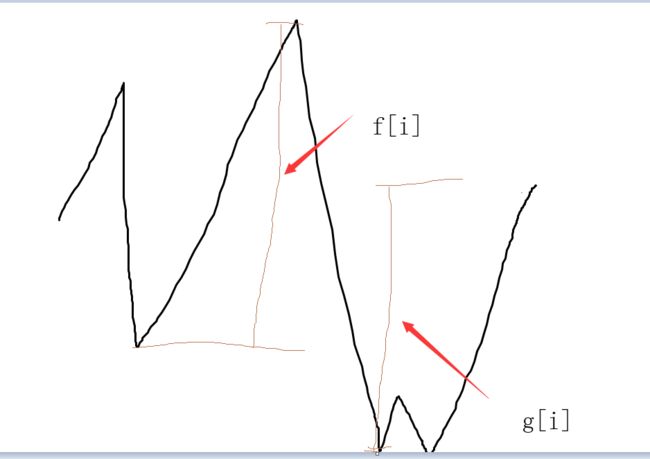
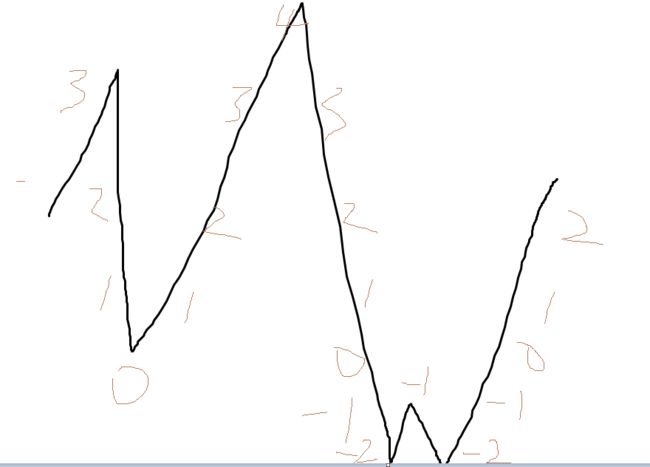
3286、[中等]穿越网格图的安全路径1、题目描述给你一个mxn的二进制矩形grid和一个整数health表示你的健康值。你开始于矩形的左上角(0,0),你的目标是矩形的右下角(m-1,n-1)。你可以在矩形中往上下左右相邻格子移动,但前提是你的健康值始终是正数。对于格子(i,j),如果grid[i][j]=1,那么这个格子视为不安全的,会使你的健康值减少1。如果你可以到达最终的格子,请你返回tr
- 2021 CCF 非专业级别软件能力认证第一轮(CSP-J1)入门级C++语言试题 (第三大题:完善程序 代码)
mmz1207
c++csp
最近有一段时间没更新了,在准备CSP考试,请大家见谅。(1)有n个人围成一个圈,依次标号0到n-1。从0号开始,依次0,1,0,1...交替报数,报到一的人离开,直至圈中剩最后一个人。求最后剩下的人的编号。#includeusingnamespacestd;intf[1000010];intmain(){intn;cin>>n;inti=0,cnt=0,p=0;while(cnt#includeu
- 放松的一天
4da9b7687fa0
20190325总结起床07:20图片发自App睡觉:23:00天气:晴今日任务清单学习·信息·阅读•水滴阅读Day40Alice’sAdventuresinWonderlandChapter6.2图片发自App•BBC跟读训练营Day24图片发自App图片发自App图片发自App•潘多拉口语训练营Day6Wow.Whatabigboy!•文化知识学习今日无•阅读时间地狱健康·饮食·锻炼•饮食目标
- 关于旗正规则引擎下载页面需要弹窗保存到本地目录的问题
何必如此
jsp超链接文件下载窗口
生成下载页面是需要选择“录入提交页面”,生成之后默认的下载页面<a>标签超链接为:<a href="<%=root_stimage%>stimage/image.jsp?filename=<%=strfile234%>&attachname=<%=java.net.URLEncoder.encode(file234filesourc
- 【Spark九十八】Standalone Cluster Mode下的资源调度源代码分析
bit1129
cluster
在分析源代码之前,首先对Standalone Cluster Mode的资源调度有一个基本的认识:
首先,运行一个Application需要Driver进程和一组Executor进程。在Standalone Cluster Mode下,Driver和Executor都是在Master的监护下给Worker发消息创建(Driver进程和Executor进程都需要分配内存和CPU,这就需要Maste
- linux上独立安装部署spark
daizj
linux安装spark1.4部署
下面讲一下linux上安装spark,以 Standalone Mode 安装
1)首先安装JDK
下载JDK:jdk-7u79-linux-x64.tar.gz ,版本是1.7以上都行,解压 tar -zxvf jdk-7u79-linux-x64.tar.gz
然后配置 ~/.bashrc&nb
- Java 字节码之解析一
周凡杨
java字节码javap
一: Java 字节代码的组织形式
类文件 {
OxCAFEBABE ,小版本号,大版本号,常量池大小,常量池数组,访问控制标记,当前类信息,父类信息,实现的接口个数,实现的接口信息数组,域个数,域信息数组,方法个数,方法信息数组,属性个数,属性信息数组
}
&nbs
- java各种小工具代码
g21121
java
1.数组转换成List
import java.util.Arrays;
Arrays.asList(Object[] obj); 2.判断一个String型是否有值
import org.springframework.util.StringUtils;
if (StringUtils.hasText(str)) 3.判断一个List是否有值
import org.spring
- 加快FineReport报表设计的几个心得体会
老A不折腾
finereport
一、从远程服务器大批量取数进行表样设计时,最好按“列顺序”取一个“空的SQL语句”,这样可提高设计速度。否则每次设计时模板均要从远程读取数据,速度相当慢!!
二、找一个富文本编辑软件(如NOTEPAD+)编辑SQL语句,这样会很好地检查语法。有时候带参数较多检查语法复杂时,结合FineReport中生成的日志,再找一个第三方数据库访问软件(如PL/SQL)进行数据检索,可以很快定位语法错误。
- mysql linux启动与停止
墙头上一根草
如何启动/停止/重启MySQL一、启动方式1、使用 service 启动:service mysqld start2、使用 mysqld 脚本启动:/etc/inint.d/mysqld start3、使用 safe_mysqld 启动:safe_mysqld&二、停止1、使用 service 启动:service mysqld stop2、使用 mysqld 脚本启动:/etc/inin
- Spring中事务管理浅谈
aijuans
spring事务管理
Spring中事务管理浅谈
By Tony Jiang@2012-1-20 Spring中对事务的声明式管理
拿一个XML举例
[html]
view plain
copy
print
?
<?xml version="1.0" encoding="UTF-8"?>&nb
- php中隐形字符65279(utf-8的BOM头)问题
alxw4616
php中隐形字符65279(utf-8的BOM头)问题
今天遇到一个问题. php输出JSON 前端在解析时发生问题:parsererror.
调试:
1.仔细对比字符串发现字符串拼写正确.怀疑是 非打印字符的问题.
2.逐一将字符串还原为unicode编码. 发现在字符串头的位置出现了一个 65279的非打印字符.
- 调用对象是否需要传递对象(初学者一定要注意这个问题)
百合不是茶
对象的传递与调用技巧
类和对象的简单的复习,在做项目的过程中有时候不知道怎样来调用类创建的对象,简单的几个类可以看清楚,一般在项目中创建十几个类往往就不知道怎么来看
为了以后能够看清楚,现在来回顾一下类和对象的创建,对象的调用和传递(前面写过一篇)
类和对象的基础概念:
JAVA中万事万物都是类 类有字段(属性),方法,嵌套类和嵌套接
- JDK1.5 AtomicLong实例
bijian1013
javathreadjava多线程AtomicLong
JDK1.5 AtomicLong实例
类 AtomicLong
可以用原子方式更新的 long 值。有关原子变量属性的描述,请参阅 java.util.concurrent.atomic 包规范。AtomicLong 可用在应用程序中(如以原子方式增加的序列号),并且不能用于替换 Long。但是,此类确实扩展了 Number,允许那些处理基于数字类的工具和实用工具进行统一访问。
- 自定义的RPC的Java实现
bijian1013
javarpc
网上看到纯java实现的RPC,很不错。
RPC的全名Remote Process Call,即远程过程调用。使用RPC,可以像使用本地的程序一样使用远程服务器上的程序。下面是一个简单的RPC 调用实例,从中可以看到RPC如何
- 【RPC框架Hessian一】Hessian RPC Hello World
bit1129
Hello world
什么是Hessian
The Hessian binary web service protocol makes web services usable without requiring a large framework, and without learning yet another alphabet soup of protocols. Because it is a binary p
- 【Spark九十五】Spark Shell操作Spark SQL
bit1129
shell
在Spark Shell上,通过创建HiveContext可以直接进行Hive操作
1. 操作Hive中已存在的表
[hadoop@hadoop bin]$ ./spark-shell
Spark assembly has been built with Hive, including Datanucleus jars on classpath
Welcom
- F5 往header加入客户端的ip
ronin47
when HTTP_RESPONSE {if {[HTTP::is_redirect]}{ HTTP::header replace Location [string map {:port/ /} [HTTP::header value Location]]HTTP::header replace Lo
- java-61-在数组中,数字减去它右边(注意是右边)的数字得到一个数对之差. 求所有数对之差的最大值。例如在数组{2, 4, 1, 16, 7, 5,
bylijinnan
java
思路来自:
http://zhedahht.blog.163.com/blog/static/2541117420116135376632/
写了个java版的
public class GreatestLeftRightDiff {
/**
* Q61.在数组中,数字减去它右边(注意是右边)的数字得到一个数对之差。
* 求所有数对之差的最大值。例如在数组
- mongoDB 索引
开窍的石头
mongoDB索引
在这一节中我们讲讲在mongo中如何创建索引
得到当前查询的索引信息
db.user.find(_id:12).explain();
cursor: basicCoursor 指的是没有索引
&
- [硬件和系统]迎峰度夏
comsci
系统
从这几天的气温来看,今年夏天的高温天气可能会维持在一个比较长的时间内
所以,从现在开始准备渡过炎热的夏天。。。。
每间房屋要有一个落地电风扇,一个空调(空调的功率和房间的面积有密切的关系)
坐的,躺的地方要有凉垫,床上要有凉席
电脑的机箱
- 基于ThinkPHP开发的公司官网
cuiyadll
行业系统
后端基于ThinkPHP,前端基于jQuery和BootstrapCo.MZ 企业系统
轻量级企业网站管理系统
运行环境:PHP5.3+, MySQL5.0
系统预览
系统下载:http://www.tecmz.com
预览地址:http://co.tecmz.com
各种设备自适应
响应式的网站设计能够对用户产生友好度,并且对于
- Transaction and redelivery in JMS (JMS的事务和失败消息重发机制)
darrenzhu
jms事务承认MQacknowledge
JMS Message Delivery Reliability and Acknowledgement Patterns
http://wso2.com/library/articles/2013/01/jms-message-delivery-reliability-acknowledgement-patterns/
Transaction and redelivery in
- Centos添加硬盘完全教程
dcj3sjt126com
linuxcentoshardware
Linux的硬盘识别:
sda 表示第1块SCSI硬盘
hda 表示第1块IDE硬盘
scd0 表示第1个USB光驱
一般使用“fdisk -l”命
- yii2 restful web服务路由
dcj3sjt126com
PHPyii2
路由
随着资源和控制器类准备,您可以使用URL如 http://localhost/index.php?r=user/create访问资源,类似于你可以用正常的Web应用程序做法。
在实践中,你通常要用美观的URL并采取有优势的HTTP动词。 例如,请求POST /users意味着访问user/create动作。 这可以很容易地通过配置urlManager应用程序组件来完成 如下所示
- MongoDB查询(4)——游标和分页[八]
eksliang
mongodbMongoDB游标MongoDB深分页
转载请出自出处:http://eksliang.iteye.com/blog/2177567 一、游标
数据库使用游标返回find的执行结果。客户端对游标的实现通常能够对最终结果进行有效控制,从shell中定义一个游标非常简单,就是将查询结果分配给一个变量(用var声明的变量就是局部变量),便创建了一个游标,如下所示:
> var
- Activity的四种启动模式和onNewIntent()
gundumw100
android
Android中Activity启动模式详解
在Android中每个界面都是一个Activity,切换界面操作其实是多个不同Activity之间的实例化操作。在Android中Activity的启动模式决定了Activity的启动运行方式。
Android总Activity的启动模式分为四种:
Activity启动模式设置:
<acti
- 攻城狮送女友的CSS3生日蛋糕
ini
htmlWebhtml5csscss3
在线预览:http://keleyi.com/keleyi/phtml/html5/29.htm
代码如下:
<!DOCTYPE html>
<html>
<head>
<meta charset="UTF-8">
<title>攻城狮送女友的CSS3生日蛋糕-柯乐义<
- 读源码学Servlet(1)GenericServlet 源码分析
jzinfo
tomcatWebservlet网络应用网络协议
Servlet API的核心就是javax.servlet.Servlet接口,所有的Servlet 类(抽象的或者自己写的)都必须实现这个接口。在Servlet接口中定义了5个方法,其中有3个方法是由Servlet 容器在Servlet的生命周期的不同阶段来调用的特定方法。
先看javax.servlet.servlet接口源码:
package
- JAVA进阶:VO(DTO)与PO(DAO)之间的转换
snoopy7713
javaVOHibernatepo
PO即 Persistence Object VO即 Value Object
VO和PO的主要区别在于: VO是独立的Java Object。 PO是由Hibernate纳入其实体容器(Entity Map)的对象,它代表了与数据库中某条记录对应的Hibernate实体,PO的变化在事务提交时将反应到实际数据库中。
实际上,这个VO被用作Data Transfer
- mongodb group by date 聚合查询日期 统计每天数据(信息量)
qiaolevip
每天进步一点点学习永无止境mongodb纵观千象
/* 1 */
{
"_id" : ObjectId("557ac1e2153c43c320393d9d"),
"msgType" : "text",
"sendTime" : ISODate("2015-06-12T11:26:26.000Z")
- java之18天 常用的类(一)
Luob.
MathDateSystemRuntimeRundom
System类
import java.util.Properties;
/**
* System:
* out:标准输出,默认是控制台
* in:标准输入,默认是键盘
*
* 描述系统的一些信息
* 获取系统的属性信息:Properties getProperties();
*
*
*
*/
public class Sy
- maven
wuai
maven
1、安装maven:解压缩、添加M2_HOME、添加环境变量path
2、创建maven_home文件夹,创建项目mvn_ch01,在其下面建立src、pom.xml,在src下面简历main、test、main下面建立java文件夹
3、编写类,在java文件夹下面依照类的包逐层创建文件夹,将此类放入最后一级文件夹
4、进入mvn_ch01
4.1、mvn compile ,执行后会在