编译原理-文法基础

概述

编译程序：将高级语言的源程序翻译成与之等价的低级语言的目标程序的这样一种程序

源程序运行过程：编译阶段+运行阶段或者编译阶段+汇编阶段+运行阶段

解释程序：以源程序作为输入，但不产生目标程序，解释一条执行一条

汇编程序：用于特定计算机上的汇编语言的翻译程序。有时编译器把汇编语言作为目标语言，然后再由汇编程序将它翻译成目标代码。

连接程序：将分别在不同的目标文件中编译或汇编的代码收集到一个可直接执行的文件中

装入程序：编译器、汇编程序或连接程序生成的代码还不能运行，装入程序处理所有的与指定的基地址有关的可重定位地址，并将修改后的指令和数据放在内存中适当的位置。

预处理程序：预处理程序是在真正的编译开始之前由编译器调用的独立程序。预处理程序可以删除注释、包含其它文件以及执行宏替代。

源程序+初始数据→解释程序→计算结果

源程序→编译程序→初始数据+目标程序+运行系统子程序→计算结果

编译过程

一般分为5个阶段：词法分析→语法分析→语义分析与中间代码产生→优化→目标代码生成

• 词法分析：按照语言的词法规则使用特定的工具将源程序转换成单词符号串
• 语法分析：按照语法规则使用上下文无关文法、确定的下推自动机将单词符号串转换为各类语法范畴 （层次结构分析）
• 语义分析与中间代码产生：按照语义规则使用属性文法将语法范畴进行初步翻译、产生中间代码（中间代码即独立于具体硬件的记号系统，四元式、三元式、逆波兰式等。）
• 优化：按照等价变换规则使用变换方法将中间代码变为更高效的中间代码
• 目标代码生成：将中间代码转换成依赖于机器的目标代码

表格管理程序：登记源程序的各类信息和编译程序各阶段的进展情况，如符号表。

出错处理程序：发现并指出源程序中错误的性质和位置；自动校正错误

遍：对源程序或源程序的中间结果从头至尾扫描一次，并作有关的加工处理，生成新的中间结果或目标程序的处理过程称为一遍。可以把一个阶段分为若干遍，也可以把多个阶段合为一遍，通常有一遍和多遍编译程序。

前端（front end）：由与源语言有关但与目标机无关的部分组成。

后端（back end）：包括与目标机有关的部分。而一般不依赖于源语言，只与中间代码有关的编译阶段。

文法基础

程序语言是符号语言，即一个记号系统，它主要有语法、语义和语用等三方面定义。

语法：是对语言结构的定义（什么样的符号序列是合法的）。任何语言程序都可看成是一定字符集上的一字符串（有限序列），语法定义语言的词法和语法的形式规则。

• 字母表是一个有限的字符集，字符集中的字符是语言程序中可能出现的字符，它们是语言程序单词的组成部分。
• 词法规则定义了语言程序中单词符号的形成规则。即什么样的字符串是一个合法的单词。如标识符、数值常量、运算符等单词的构成规则。
• 语法规则定义了语言程序中语法单位的形成规则。一般语言的语法单位有表达式、语句、分程序、函数、过程和程序等。描述语法规则和进行语法分析的有效工具是上下文无关文法。

语义：描述语言的含义；定义语言的单词符号和语法单位的意义。目前编译程序中常用的语义分析方法是一种基于属性文法的语法制导翻译。即在语法分析的同时对其中识别出的语法单位进行语义的分析与翻译工作；在描述文法的同时为定义的语法范畴加上它们的属性计算规则，属性可以是语法范畴的类型、地址、取值、执行动作等信息。

语用：是从使用的角度去描述语言。定义程序设计技术和语言成分的使用方法，它使语言的基本概念与语言的外界（如数学概念或计算机的对象和操作）联系起来

字母表(alphabet)：字母表是元素的非空有穷集合，任何语言的字母表指出了该语言中允许出现的一切符号。

【例如】	∑ = {a,b,c}
∑是字母表，由 a,b,c 三个元素组成。
C 语言的字母表是字母、数字和若干专用符号组成。

符号(symbol)：字母表中的元素称为符号，或称为字符。

【例如】	∑ = {a,b,c}
a,b,c 是字母表 ∑ 中的符号。

符号串（string）:符号的有穷序列称为字符串。符号串总是建立在某个特定字母表上的且只能由字母表上的有穷多个符号组成。不包含任何符号的符号串，称为空符号串，用$ϵ$(epsilon)表示

【例如】设有字母表 ∑ = {a,b,c}，
则有符号串 a,b,ab,ba,cba,abc,…
(a,b,ab,ba,cba,abc 等都是字母表∑上的符号串)

符号串的连结 catenation：设 x 和 y 是符号串，则串 xy 称为它们的连结。

【例如】设 x ＝ abc，y = 10a，
则 xy ＝ abc10a
则 yx ＝ 10aabc

特别，对任意一符号串 x 有：$ϵx=xϵ=x$

集合的乘积 product：设 A 和 B 是符号串的集合，则 A 和 B 的乘积定义为：AB = {xy | x ∈ A, y ∈ B}

【例如】设 A = {a,b}, B = {c,d}
则 AB ＝ {ac,ad,bc,bd}

空集 Φ empty set：Φ 表示不含任何元素的空集 { }

符号串的幂运算 power：设 x 是符号串，则 x 的幂运算定义为：
$$x^0＝ϵ;x^1＝x;x^2＝xx\dots \dots x^n＝xx\dots x$$

集合的幂运算同理，只不过$A^0=\{ϵ\}$

集合A的正闭包A+与闭包A：设 A 是符号串的集合，则集合 A 的正闭包 A+ 和闭包 A* 定义为：
$$\begin{gathered} A^{+}＝A^{1}U{A}^{2}U{A}^{3}U\dots U{A}^{n}U\dots \\ {A}^{\ast }＝A^{0}U{A}^{1}U{A}^{2}U{A}^{3}U\dots U{A}^{n}U\dots =\{ϵ\}U{A}^{+} \end{gathered}$$

$$\begin{gathered} 【例如】设A=\{a,b\},则 \\ {A}^{+}＝\{a,b,aa,ab,ba,bb,aaa,aab,\dots \} \\ A\ast ＝\{ϵ,a,b,aa,ab,ba,bb,aaa,aab,\dots \} \end{gathered}$$

形式语言和文法

形式语言：序列(字符串)的集合称为形式语言。每个形式语言都是某个字母表上按某种规则构成的所有符号串的集合；任何一个字母表上符号串的集合均可定义一个形式语言。

【例如】
C 语言是具有基本符号字母表上的符号串的集合。每个 C 语言程序是基本符号的符号串。

形式语言的描述有两种方法：

1. 当语言为有穷集合时，用枚举法来表示语言。

【例】设有字母表 A={a,b,c},则L1 ＝ {a,b,c},L2 ＝ {a,aa,ab,ac},L3 ＝ {c,cc}均表示字母表 A 上的一个形式语言。由于这三个语言均是有限符号串的集合，可以枚举出其全部句子来表示该语言。

2. 当语言为无穷集合时，需要设计文法来描述无穷集合的语言。

$$\begin{gathered} 【例】设有字母表\sum =\{0,1\}, \\ 则\sum ^{+}＝\sum ^1\bigcup \sum 2\bigcup \sum 3\bigcup \dots =\{0,1,00,10,11,01,000,100,\dots \} \\ 用A表示\sum ^{+}，用式子A\to 0表示符号串0\in A或A生成符号串0则集合A可表示成： \\ A\to 0;A\to 1;A\to A0;A\to A1 \end{gathered}$$

显然由 A 生成的符号串属于 ∑+，这就是文法描述语言，它描述了无穷集合的语言。

文法的形式定义：

规则：规则也称产生式，它是一个符号与一个符号串的有序对（A,$\beta$），通常写做A→$\beta$（ 或 A::=$\beta$ ）

其中 A 是规则左部，是一个符号；$\beta$是规则右部，是一个符号串。→ 或 ::= 表示“定义为”或“生成”，意思是左部符号用右部符号串定义或左部符号生成右部符号串。规则的作用是告诉如何用规则中的符号串生成语言中的序列。一组规则规定了一个语言的语法结构。

非终结符：出现在产生式左部能派生出符号或符号串的那些符号，即每个非终结符表示一定符号串的集合。用大写字母表示或用尖括号把非终结符括起来。
终结符：是不属于非终结符的那些符号，它是组成语言的基本符号，是一个语言的不可再分的基本符号，只出现在产生式右部。通常用小写字母表示。

【例】产生式	A→A1 A→A0
	A 是非终结符，0、1 是终结符

文法：文法是规则的非空集合，是一个四元式G =（$V_N$，$V_T$，P，S），其中：

• $V_N$ 是一个非空有限集，它的每个元素为非终结符号，
• $V_T$ 是一个非空有限集，它的每个元素为终结符号； $V_T$ ∩ $V_N$ = Φ
• S 是一个非终结符号，称为开始符号或识别符号；开始符号 S 至少必须在某个产生式的左部出现一次。
• P 是一个产生式集合（有限），每个产生式的形式是P→α，其 P ∈ $V_N$ ， α ∈ ($V_T$∪$V_N$)*。

左部相同的产生式，如A→α1， A→α2， …， A→αn，可合并为一个，缩写为A→ α1|α2| … |αn

设计文法示例

例1

设字母表∑＝{a,b},试设计文法，描述语言 L={$a^{2n}$，$b^{2n}$ | n≥1}

分析：设计文法来描述一个语言，关键是设计一组规则生成语言中的符号串。设计语言的文法，必须分析这个语言是由怎样一些符号串组成，即首先分析语言中符号串的结构特征：

当 n=1		L = {aa,bb}
当 n=2		L = {aaaa,bbbb}
当 n=3		L = {aaaaaa,bbbbbb}
…
L = {aa,bb,aaaa,bbbb,aaaaaa,bbbbbb,…}
语言 L 是由偶数个 a，偶数个 b 这样的符号串组成的集合。

$$\begin{gathered} 文法1：G=（V_N，V_T，S，P），其中 \\ {V}_N=\{A,B,D\} \\ {V}_T=\{a,b\} \\ P=\{A\to aa|aaB|bb|bbD \\ B\to aa|aaB \\ D\to bb|bbD\} \\ S=A \end{gathered}$$

很显然，a,b是终结符，非终结符A定义完整L，需要终结符B、D来描述A，按照逻辑，该文法能描述语言L，此外，描述该语言的文法不是唯一的。
$$\begin{gathered} 文法2：G^{\prime }=（V_N，V_T，S，P），其中 \\ {V}_N=\{A,B,D\} \\ {V}_T=\{a,b\} \\ P=\{A\to B|D \\ B\to aa|aBa \\ D\to bb|bDb\} \\ S=A \end{gathered}$$
G 和 G’ 是两个的文法，如果它们描述的语言相同，那么称 G 和 G’ 为等价文法。

例2

设计一个表示所有标识符的文法

分析：标识符的定义是字母或以字母开头的字母数字串（此处先不考虑大写字母）

显然，终结符是字母数字集合{a-z}∪{0-9}中的元素，标识符语言={字母*字母,字母*数字}，因此设计文法
$$\begin{gathered} 用I表示标识符，L代表字母，D代表数字，定义标识符的文法为：G=（VN，VT，P，S）其中： \\ {V}_N=\{I,L,D\} \\ {V}_T=\{a,b,\dots ,x,y,z,0,1,2,\dots ,9\} \\ P=\{I\to L|IL|ID \\ L\to a|b|\dots |x|y|z \\ D\to 0|1|\dots |9\} \\ S=I \end{gathered}$$
例3

用文法定义一个含+、*、()的算术表达式。

分析：变量是表达式；若 E1 和 E2 是算术表达式，则 E1+E2，E1*E2，(E) 也是算术表达式。
$$\begin{gathered} G=（V_N，V_T，P，S）其中： \\ {V}_N=\{E\} \\ {V}_T=\{i,+,\ast ,(,)\} \\ P=\{E\to i|E+E|E\ast E|(E)\} \\ S=E \end{gathered}$$
例4

设字母表∑＝{a,b}，设计一个文法，描述语言 L={a$b^n$a | n≥0}
$$\begin{gathered} G=（\{A,B\}，\{a,b\}，P，A） \\ P=\{A\to aBa,B\to ϵ|Bb\} \end{gathered}$$

语言形式定义

直接推导：令 G 是一文法，一步推导 => 表示用某一规则的右部替换其左部。如果有 xAy => xαy，仅当 A→α 是 G 的一个规则（产生式），且 x、y ∈ ($V_T$∪$V_N$)，称 xAy 直接推出 xαy。
$$\begin{gathered} 【例】设有文法G[S]=(\{S\},\{0,1\},P,S) \\ 其中P为S\to 01|0S1 \\ 则可直接推导出S=>01,S=>0S1,0S1=>0011,00S11=>000S111... \end{gathered}$$
推导：如果存在一个直接推导序列：${\alpha }_0$ => ${\alpha }_1$ => … => $a_n$则称这个序列是从${\alpha }_0$ 到${\alpha }_n$ 的长度为 n 推导，记为$a_0$=>+（这个符号其实是+在=>这个符号上面，这里表示不出来，下面这个符号都用=>+表示） ${\alpha }_n$
$$\begin{gathered} 【例】设有文法G[E]=(\{E,T,F\},\{i,+,\ast ,(,)\},P,E) \\ P=\{E\to E+T|T \\ T\to T\ast F|F \\ F\to i|(E)\} \\ 则对i+i\ast i有如下直接推导序列E=>E+T=>T+T=>F+T=>i+T \\ =>i+T\ast F=>i+F\ast F \\ =>i+i\ast F=>i+i\ast i \\ 所以E=>+i+i\ast i \end{gathered}$$
广义推导：${\alpha }_0$ =>(这个符号其实是*在=>这个符号的上面，这里表示不出来，下面这个符号都用=>*表示)${\alpha }_n$ 表示从α0 出发，经过 0 步或多步可推导${\alpha }_n$,也就是说${\alpha }_0$ =>*${\alpha }_n$ 意味着： ${\alpha }_0$ =${\alpha }_n$ 或者${\alpha }_0$ =>+${\alpha }_n$

直接推导的长度为1，推导的长度大于等于1，广义推导的长度大于等于0

句型与句子：

设有文法 G[S]，如果S=>*x, x∈($V_T$∪$V_N$)*，则称符号串 x 为文法 G[S]的句型.
如果S==>*x, x∈$V_T^{\ast }$，则称符号串 x 为文法 G[S]的句子。

【例】设有文法 G[S]:	S→01 | 0S1
有
	S =>*01		句型，又是句子
	S =>*0S1		句型
	S =>*00S11		句型
	S =>*000111		句型，又是句子

【例】设有文法G[E]:E → E+E | E*E |(E) | i
试证明符号串 (i*i+i) 是文法G[E]的一个句子
分析：只要证明符号串(i*i+i) 对文法G[E]存在一个推导，就可证明符号串(i*i+i) 是文法G[E]的一个句子。
因为
E=>(E)=>(E+E)=>(E*E+E)=>(i*E+E)=>(i*i+E)=>(i*i+i)
即有 E=>*(i*i+i)
所以符号串 (i*i+i) 是文法G[E]的一个句子。

语言：

文法 G[S] 产生的所有句子的集合称为文法 G 所定义的语言，记为 L(G[S]):L(G[S]) = { x | S=>+x 且 x∈$V_T^{\ast }$ }，由语言定义可知：
(1)当文法给定，语言也就确定；
(2)L(G) 是 $V_T^{\ast }$ 的子集。即属于$V_T^{\ast }$的符号串不一定属于L(G)

文法求语言示例

例1

设有文法G[S]: S→01 | 0S1，求该文法所描述的语言

分析：问题归结为由识别符号 S 出发，将推导出什么样的句子，也就是说 L(G{S])是由一些什么样的符号串所组成的集合，找出其中的规律，用式子或自然语言描述出来。

$S=>0S1=>00S11=>000S111=>\dots =>0^{n－1}S{1}^{n－1}=>0^n{1}^n$
即S >=+ $0^n{1}^n$
所以此文法定义的语言为 L(G[E]) = {$0^n{1}^n$ | n≥1}

例2

设有文法G[S]: S→0S|1S|$\epsilon $求该文法所定义的语言
$$该文法所确定的语言为L(G[S])=\{ϵ,0,1,00,01,10,11,\dots \}=\{x|x\in \{0,1{\}}^{\ast }\}$$
例3

设有文法G[A]: A→yB,B→xB|x求该文法所定义的语言
$$\begin{gathered} 从开始符号A出发，我们可以推出如下句子： \\ A=>yB=>yx \\ A=>yB=>yxB=>yxx \\ \dots \dots \\ A=>yB=>yxB=>\dots =>yx\dots x \\ 归纳得出从A出发可推导出所有以y开头后跟一个或任意多个x得字符串，即 \\ L(G[A])=\{y{x}^n|n\ge 1\} \end{gathered}$$

规范推导和规范归约

文法所定义的任一句型和句子，都可以根据文法推导出来，但同一个句型(句子)可以通过不同的推导序列推导出来，这是因为在推导过程中所选择非终结符的次序无关。

【例】设有文法 G[N1]:N1 → N,N → ND | D,D → 0 | 1 | 2
该文法所定义的语言是由数字 0，1，2组成的所有无符号整数。符号串 12 是该文法的一个句子，它可以通过下列不同的推导序列推导出来：
(1)		N1 =>N=>ND=>N2=>D2=>12
(2)		N1 =>N=>ND=>DD=>1D=>12
(3)		N1 =>N=>ND=>DD=>D2=>12

为了使句子能按一种确定的推导序列来产生，以便对句子的结构进行确定性的分析。通常只考虑两种特殊推导：

• 最左推导是指对于一个推导序列中的每一步直接推导 α=>β，都对 α 中的最左非终结符进行替换。
• 最右推导是指对于一个推导序列中的每一步直接推导 α=>β，都对 α 中的最右非终结符进行替换。

最右推导也称为规范推导，用规范推导推导出的句型称为规范句型。每个句子都有规范推导，但对句型此结论并不成立。

【例】对文法 G[N]:N →N’, N’→D | N’D, D →0 | 1 | 2 | … | 9
N=>N’=>N’D=>N’8=>D8=>88	规范推导
N=>N’=>N’D=>DD=>8D=>88	不是规范推导

归约：推导的逆过程。归约是与推导相对的概念，推导是把句型中的非终结符用规则的一个右部来替换的过程，而归约是句型中的某个子串用一个非终结符来替换的过程.用 =>· （实际上·在=>这个符号上面，下面均用=>·表示这个符号）表示归约。

【例】设 A→α是文法 G 的一个规则，则有
	xAy => xαy
	xαy  =>· xAy

【例】设有文法 G[S]:S→AB, A→A0 | 1B, B→0 | S1
请给出句子 101001 的最左和最右推导。
分析：
最右推导是指在推导过程中任何一步α=>β(α和β都是句型)，都是对α中的最右非终结符进行替换。
S=>AB=>AS1=>AAB1=>AA01=>A1B01=>A1001=>1B1001=>101001
最左推导是指在推导过程中任何一步α=>β(α和β都是句型)，都是对α中的最左非终结符进行替换。
S=>AB=>1BB=>10B=>10S1=>10AB1=>101BB1=>1010B1=>101001

规范推导的逆过程，称为最左归约，也称为规范归约。

【例】	文法G[N1]=N1 → N, N → ND | D,	D → 0 | 1 | 2
规范推导
	N1 =>N=>ND=>N2=>D2=>12
则有规范归约
	12=>·D2=>·N2=>·ND=>·N=>·N1 

递归规则与文法的递归性

递归规则：所谓递归规则，是指在规则的左部和右部具有相同的非终结符的规则。

如果文法中有规则 A→A... 	称为规则左递归
如果文法中有规则 A→...A 	称为规则右递归
如果文法中有规则 A→...A... 称为规则递归

文法的递归性：文法的递归性，是指对文法中任一非终结符，若能建立一个推导过程，在推导所得的符号串中又出现了该非终结符本身，则文法是递归的，否则是无递归性的。

若文法中有推导 A =>+ A... 	称为文法左递归
若文法中有推导 A =>+ ...A.. 	称为文法右递归
若文法中有推导 A =>+ ...A... 	称为文法递归

文法中使用递归规则，使得能用有限的规则去定义无穷集合的语言。

文法中有如下规则：
	U →Vx
	V →Uy | z
显然规则都不是递归规则，
但	U =>+ Uyx，则该文法是左递归的。

考虑文法 G[A]:
	A → aB | bB
	B → a | b
该文法无递归性，由它描述的语言是有穷的。L(G[A]) = {aa,ab,ba,bb}

$$\begin{gathered} 考虑文法G[N1]:N1\to N,N\to ND|D,D\to 0|1|2 \\ 分析:该文法有直接左递归规则N\to ND，则称该文法为左递归文法或称文法左递归。 \\ L(G[N1])=\{x|x\in \{0,1,2{\}}^{+}\} \end{gathered}$$

• 文法中使用了递归规则，使得可用有限的规则去刻画无穷集合的语言。
• 若不用递归规则来定义文法，需要用无穷多条规则去表示无穷集合的语言
• 当一个语言是无穷集合时，则定义该语言的文法一定是递归的。
• 程序设计语言都是无穷集合，因此描述它们的文法必定是递归的。

短语、直接短语和句柄

令 G 是一个文法，S 是文法的开始符号，假定αβδ是文法 G 的一个句型，如果是
S =>* αAδ 且 A =>+ β
则称 β 是相对于非终结符 A 的句型 αβδ 的短语。
特别是，如果有
S =>* αAδ 且 A => β
则称β是直接短语（简单短语）。

短语是句型的一部分。
$$\begin{gathered} 考虑文法G[N1]:N1\to N \\ N\to ND|D \\ D\to 0|1|2 \\ 对于句型ND \\ (1)N1=>\ast N \\ N1=>\ast ϵNϵ \\ (2)N=>+ND \\ 所以ND是句型ND的短语，并且是直接短语 \end{gathered}$$
一个句型的最左直接短语称为该句型的句柄。
句柄特征：
(1)它是直接短语，即某规则右部
(2)它具有最左性。

短语、直接短语和句柄都是针对某一句型的，特指句型中的哪些符号串能构成短语和直接短语，离开具体的句型来谈短语、直接短语和句柄是无意义的。.

设有文法G[S]=({S,A,B},{a,b},P,S) S →AB A →Aa | bB B →a|Sb 求句型 baSb 的全部短语、直接短语和句柄

根据短语定义，可以从句型的推导过程中找出其全部短语、直接短语和句柄。建立句型的推导过程：
S=>AB=>bBB=>baB=>baSb 最左推导
S=>AB=>ASb=>bBSb=>baSb 最右推导

语法树/推导树

对句型的推导过程给出一种图形表示，这种图形表示称为语法树，也称推导树。设文法 G=($V_N$，$V_T$，S，P)，对 G 的任何句型都能构造与之关联的、满足下列条件的一棵语法树。

• 每个结点都有一个标记，此标记是V＝$V_N$∪$V_T$∪{$ϵ$}中的一个符号。树
• 根的标记是文法的开始符号 S。
• 若某一结点至少有一个分支结点，则该结点上的标记一定是非终结符。
• 若 A 的结点有 k 个分支结点，其分支结点的标记分别为 A1,A2,…Ak,则 A→A1A2…Ak一定是G的一条规则

【例】设有文法 G[E] = ({E,T,F},{i,+,-,*,/,(,)},P,E)
其中P 为E → E+T | E-T | T;	T → T*F | T/F |F;  F → (E) | i
根据推导，画出句型 (i+i)*i-i 的语法树 

语法树的构造是从文法的开始符号出发，构造一个推导的过程，因为文法的每一个句型(句子)都存在一个推导，所以文法的每个句型(句子)都有一棵对应的语法树。

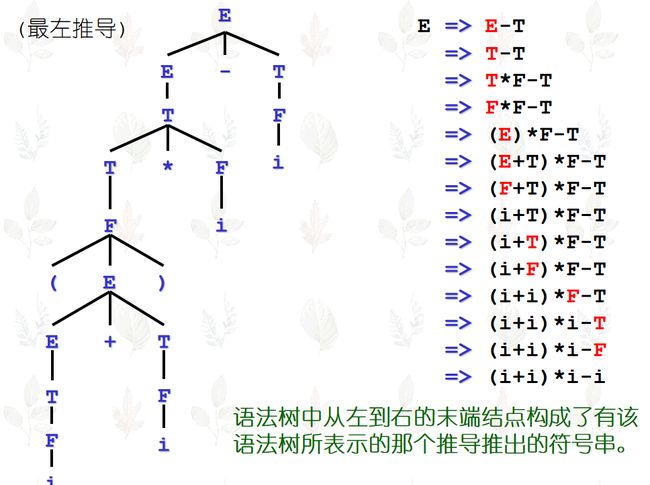
句型 (i+i)*i-i 的最左、最右推导得到的语法树完全相同，也就是说，一棵语法树表示一个句型的种种可能的(但未必是所有的)不同推导过程。

子树：语法树的子树是由某一个结点连同所有分支组成的部分。

简单子树：语法树的简单子树是指只有单层分支的子树。

根据子树的概念，句型的短语、直接短语和句柄的直观解释如下：

短语：子树的末端结点形成的符号串是相对于子树根的短语。
直接短语：简单子树的末端结点形成的符号串是相对于简单子树根的直接短语。
句柄：最左简单子树的末端结点形成的符号串是句柄。

因此可以由子树以及子树的末端节点直接看出短语、直接短语与句柄

文法的二义性

如果一个文法存在某个句子对应两棵不同的语法树，则称这个文法是二义的。也就是说，若一个文法存在某个句子，它有两个不同的最左推导或有两个不同的最右推导，则称这个文法是二义的

二义性的文法将给编译程序的执行带来问题。对于二义性文法的句子，当编译程序对它的结构进行语法分析时，就会产生两种甚至多种不同的理解。语法结构上的不确定性，必将导致语义处理上的不确定性。

解决二义性问题：构造一个等价的无二义性文法；即排除二义性的规则，改写原有的文法。

在改造文法的过程中，观察到推导步骤中的规律：靠前的推导，所用规则结合性弱；语法树上层次高；靠后的推导，所用规则结合性强，语法树上层次低。

也就是说，想要让一个规则结合性弱；就让它出现在推导序列前面（语法树的上层）；想要让一个规则结合性强；就让它出现在推导序列后面（语法树的下层），对于这样的强弱规律正好对应于运算的优先级规律，因此将运算符的优先顺序和结合规则，融合到原有文法中，可构造出无二义性文法

【例】对于文法 G：E → E + E | E﹡E | (E) |i
按照终结符优先级的规律，可以构造出无二义性文法 G’[E] 如下：
		E → E + T | T	
        T → T * F | F		
        F → (E) | i		

改造之后的语法树就变为了：

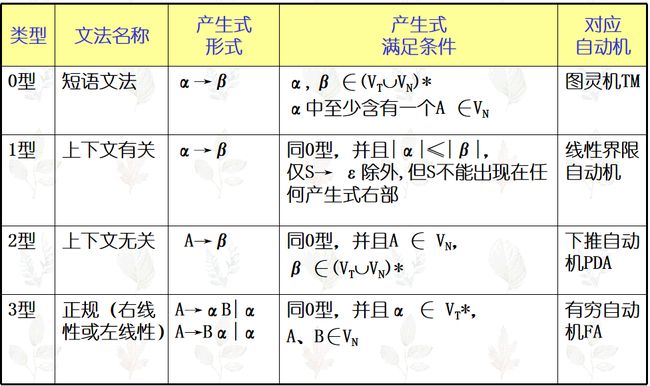
文法种类

2 型文法(上下文无关文法)

若文法 G=($V_N$，$V_T$，S，P)中的每条规则 A → β，其中 A∈$V_N$，β∈($V_T$∪$V_N$)*，则称 G 是 2 型文法，2 型文法描述的语言是 2型语言

由定义可见，利用规则将 A 替换成 β 时，与 A 的上下文环境无关，即无需考虑 A 在上下文中出现的情况。故又称为上下文无关文法，相应的语言称为上下文无关语言。
通常定义程序设计语言的文法是上下文无关文法。

3 型文法(正规文法)

右线形文法：若文法G=($V_N$，$V_T$，S，P)中的每条规则A → αB 或 A → α，其中 A,B∈$V_N$，α∈$V_T$，则称 G 是右线形文法。
左线形文法：若文法G=($V_N$，$V_T$，S，P)中的每条规则A → Bα 或 A → α，其中 A,B∈$V_N$，α∈$V_T$，则称 G 是左线形文法。

右线形文法和左线形文法都称为 3 型文法或正规文法，3型文法描述的语言称为 3 型语言或正规语言。通常定义程序设计语言词法规则的文法是正规文法。