图解 C语言实现数据结构 栈

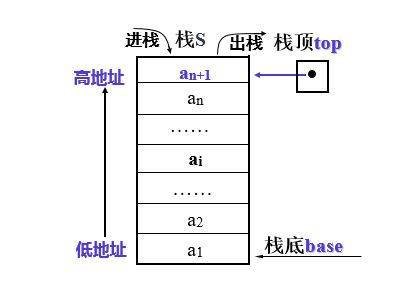
栈是仅在表尾进行插入、删除操作的线性表。即栈 S= (a1, a2, a3, ………,an-1, an)，其中表尾(即 an 端)称为栈顶 /top，表头(即 a1 端)称为栈底/base。

由于只能在表尾进行操作，因此栈的运算规则就是“后进先出”(LIFO)

提起栈，最常见的用途就是调用函数了，例如JS里面的执行栈，但是栈可以用于递归运算、简化程序等等。

和线性表类似，栈也有两种存储结构——顺序栈与链栈

栈的顺序存储结构——顺序栈

顺序栈的表示与实现

用C语言表示栈的顺序结构

#define STACK_INIT_SIZE 100 #define STACKINCREMENT 10 typedef struct { SElemType *base; // 栈底指针（始终指向栈底） SElemType *top; // 栈顶指针 int stacksize; // 当前栈的最大容量 } SqStack;

用下图表示就是

小编推荐一个学C语言/C++的学习裙六六六二九五四九八 邀请编码【凌云】无论你是大牛还是小白，是想转行还是想入行都可以来了解一起进步一起学习！裙内有开发工具，很多干货和技术资料分享！

其中: 1. s.base 始终指向栈底 2. s.top 始终指向栈顶元素的下一个位置 3. s.base = NULL 表示栈结构不存在 4. s.top = s.base 表示栈空 5. top-base = stacksize 表示栈满

顺序栈的基本操作

1. 初始化栈

Status initStack(SqStack *S) { S.base = (SElemType *)malloc(STACK_INIT_SIZE*sizeof(ElemType)); if(!S.base) return ERROR; S.top = S.base; S.stacksize = STACK_INIT_SIZE; return OK; }

2. 栈判空

Status stackEmpty(SqStack* S) { return S.top == S.base; }

3. 判栈满

Status stackFull(SqStack* S) { return ((S.top - S.base) == S.stacksize); }

4. 读取栈顶元素

Status getTop(SqStack* S, ElemType e) {//返回栈S的栈顶元素,但栈顶指针保持不变 if(S.top == S.base) //栈为空 {printf("Stack is empty!"); return ERROR; } e = *(S.top-1); return OK; }

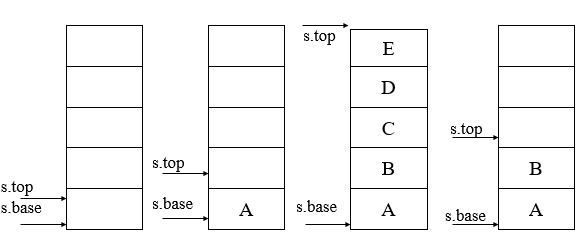
5. 入栈

Status push(SqStack* S, SElemType e) { if(S.top-S.base >= S.stacksize) //判满 { //追加存储空间 S.base = (ElemType*)realloc(S.base(S.stacksize+STACKINCREMENT)*sizeof(ElemType)); if(!S.base) exit(OVERFLOW); //上溢 S.top = S.base+S.stacksize; S.stacksize += STACKINCREMENT; } *S.top++ = e; //栈顶指针后移，赋值 return OK; }

6. 出栈

Status pop(SqStack* S, SElemType *e) { //将栈S的栈顶元素弹出并返回 if(S.top == S.base) { printf("Stack is empty!"); return ERROR; } e = s->top; s->top--; return OK; }

栈的链式存储结构——链栈

栈的链式存储结构,也称为链栈，它是一种限制运算的链表，即规定链表中的插入和删除运算只能在链表开头进行。

链栈的表示与实现

用C语言表示栈的链式结构

typedef struct SNode { SElemType data; struct SNode *next; }SNode, *LinkStack

链栈的基本操作

1. 初始化栈

void iniStack(LinkStack* top) { top = (LinkStack*)malloc(sizeof(SNode)); top->next = NULL; }

2. 进栈

Status push(LinkStack* top, SElemType e) { LinkStack* q; q = (LinkStack*)malloc(sizeof(SNode)); if (!q) exit(OVERFLOW); //存储分配失败 q->data = e; q->next = top->next; top->next = q; return OK; }

3. 出栈

Status pop(LinkStack* top, SElemType e) { LinkStack* q; if (!top->next) return ERROR; e = top->next->data; //取出栈顶元素的值 q = top->next; //q指向栈顶元素 top->next = q->next; //删除栈顶元素 free (q); //释放栈顶元素所占的空间 return OK; }

4.取栈顶元素

Status getTop(LinkStack* top, SElemType e) { if (!top->next) return ERROR; else { e = top->next->data; return OK; } }

栈的典型应用

栈的典型应用，包括数字转换问题、括号匹配问题、表达式求值、递归中的汉诺塔等等。

这里用栈对表达式求值做一个很简单的解释。

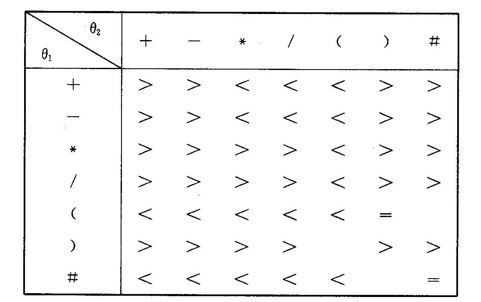
编写算法，用栈实现表达式3 * (7 - 2)求值。一个算术表达式是由操作数(x，y，z…)和算符(*, /, +, -, (, ), #)组成。其中算法规则是：1. 从左算到右; 2. 先乘除, 后加减; 3. 先括号内, 后括号外.

其中算符之间的优先级如下图

在这个问题中，算法的思想是：

为了实现算符优先算法，可以设定两个工作栈，OPND—存放操作数或运算结果，OPTR—存放运算符号。

1) 首先置操作数栈OPND为空栈，表达式的起始符#为运算符栈OPTR的栈底元素；

2) 依次读入表达式中的每个字符，若运算符是 “#” 且栈顶是 “#”，结束计算，返回OPND栈顶值。如果是操作数，则push(OPND，操作数)，如果是运算符，则与OPTR栈顶元素进行比较，按优先级进行操作。

算法的实现，伪代码形式。

OperandType eval() { initstack(&OPTR); //初始化OPTR栈 push(&OPTR, '#'); initstack(&OPND); c = getchar(); while (c != '#') || getTop(OPTR) != '#') { if (!in(c,op)) //如果c是操作数 { push(&OPND); c = getchar(); } else //c是一个运算符 { r=precede(getTop(OPTR), c); // 比较两个运算符的优先级 switch(r) { case '': //退栈并将运算结果入栈 pop(&OPTR,&op); pop(&OPND,&b); pop(&OPND,&a); value=operate(a, op, b) ; push(&OPND, value); break; } } } return(getTop(OPND)); }

用一张图来表示这个过程就是

栈的另一个重要的用途就是递归，在这里就不细说了