牛客寒假算法基础集训营1(部分)
链接:https://ac.nowcoder.com/acm/contest/317/A
来源:牛客网
小a的计算器
题目描述
小a的数学基础实在太差了,以至于他只会用计算器算数。他的计算器比较特殊,只有+,−,×,/(即加减乘除)四种运算。
经过一番周折,小a终于算出了他想要的数,但是他却忘记了最初的数是什么。不过幸运的是他记下了整个操作序列,他想请你帮他算出最初的数
输入描述:
第一行两个整数n,X,分别表示操作次数和最终的数
接下来nn行表示操作序列,每行两个数opt,x
若opt=1,则表示将当前数加x
若opt=2,则表示将当前数减x
若opt=3,则表示将当前数乘x
若opt=4,则表示将当前数除以x输出描述:
一个整数表示最初的数示例1
输入
复制
4 6
1 3
2 1
3 3
4 2输出
复制
2说明
样例1解释
2+3=5
5−1=4
4∗3=12
12/2=6
示例2
输入
3 292
3 2
4 3
4 3输出
1314备注:
n⩽100,0#include
#include
#include
#include
#include
#include
#include
#include
#define Swap(a,b) a ^= b ^= a ^= b
using namespace std ;
const int MAX = 10005;
const int inf = 0xffffff;
const int mod = 1e9+7 ;
typedef long long LL;
int minn = 0x3f3f3f3f ;
int maxx = -0x3f3f3f3f;
int ans ;
// --------------------------------
LL gcd(LL a , LL b)
{
return b== 0 ? a : gcd(b,a%b) ;
}
struct node {
int opt ;
LL x ;
};
int main()
{
LL n , X ;
node a[MAX] ;
stack s ;
LL ans ;
cin >> n >> X ;
for(int i = 1 ; i<=n ; i++ )
{
cin >>a[i].opt >> a[i].x ;
s.push(a[i]) ;
}
while(!s.empty())
{
node tmp = s.top() ;
s.pop() ;
//cout<
链接:https://ac.nowcoder.com/acm/contest/317/B
来源:牛客网
小a与"204"
题目描述
小a非常喜欢204这个数字,因为′a′+′k′=204';
现在他有一个长度为n的序列,其中只含有2,0,4这三种数字
设ai为序列中第i个数,你需要重新排列这个数列,使得∑ni=1(ai−ai−1)2最大(公式的含义是:每个数与前一个数差的平方的和)
注意:我们默认a0=0
输入描述:
第一行一个整数n
接下来一行n个整数,第i个数表示ai输出描述:
输出一个整数,表示∑ni=1(ai−ai−1)2的最大值示例1
输入
复制
2
2 4输出
复制
20说明
样例1解释:按(4,2)排列是最优的,此时sum=(4−0)2+(2−4)2=20示例2
输入
复制
3
2 0 4输出
复制
36说明
样例2解释:按(4,0,2)排列是最优的,此时sum=(4−0)2+(0−4)2+(2−0)2=36示例3
输入
复制
5
2 4 0 2 4输出
复制
52备注:
1⩽n⩽105,保证ai为2/0/4中的数牛客给出的题解:
输入的序列其实用处不大,因为最终不需要输出方案,我们只需要记录下2/0/4分别出现的次数即可 一个显然的构造策略是首先放置4, 0, 4, 0,直到其中一个用光。 接下来如果4多余,那么可以按4,0,4,0,…,4,2,4,2,…(先4后2)的方法构造 如果0多余,可以按照4,0,4,0 … 4,0,2,0,2 …(先2后0)的方法构造 std中的a数组展示了其中一种最优的构造方案 实际上此题还可以推广到更一般的情况,也就是第一个位置放最大的,第二个位置放最小的,第三个位置放 第二大的以此类推,这种思路写起来也会更简单一
我是模拟的,太乱了(emmm)
#include
#include
#include
#include
#include
#include
#include
#include
#define Swap(a,b) a ^= b ^= a ^= b
using namespace std ;
const int MAX = 100005;
const int inf = 0xffffff;
const int mod = 1e9+7 ;
typedef long long LL;
int minn = 0x3f3f3f3f ;
LL maxx = -0x3f3f3f3f;
// --------------------------------
LL gcd(LL a , LL b)
{
return b== 0 ? a : gcd(b,a%b) ;
}
int a[MAX] ;
int book[5] ;
int main()
{
int n ;
cin >>n ;
for(int i = 1 ; i <=n ; i++ )
{
cin >> a[i] ;
book[a[i]]++ ;
}
int ans = 0 ;
if(book[4] == 0 && book[0] == 0 )
{
cout<<"4"<b)
{
ans+=b*8 ;
c-=b;
b-=b;
}
else if (c == b)
{
ans+=(b*8) ;
c-=c ;
b-=b ;
}
else{
ans+=(c*8);
c-=c ;
b-=c;
if(b)
{
ans+=4 ;
b-=b;
}
}
}
else if (a == c )
{
ans+=(a*32) ;
a-=a ;
c-=c ;
if(b)
{
ans+=4 ;
b-=b;
}
}
else{
// a >c ;
ans+=(c*32) ;
a-=c;
c-=c;
if(b > a)
{
ans+=(a*8);
b-=a;
a-=a;
if(b)
{
ans+=4 ;
b-=b;
}
}
else if (a == b)
{
ans+=(a*8) ;
b-=b;
a-=a;
}
else{
//b
小a与星际探索
链接:https://ac.nowcoder.com/acm/contest/317/C
来源:牛客网
题目描述
小a正在玩一款星际探索游戏,小a需要驾驶着飞船从1号星球出发前往n号星球。其中每个星球有一个能量指数p。星球ii能到达星球j当且仅当pi>pj。
同时小a的飞船还有一个耐久度tt,初始时为11号点的能量指数,若小a前往星球jj,那么飞船的耐久度会变为t⊕pj(即t异或pj,关于其定义请自行百度)
小a想知道到达n号星球时耐久度最大为多少
注意:对于每个位置来说,从它出发可以到达的位置仅与两者的p有关,与下标无关
输入描述:
第一行一个整数n,表示星球数
接下来一行有n个整数,第ii个整数表示pi输出描述:
一个整数表示到达n号星球时最大的耐久度
若不能到达n号星球或到达时的最大耐久度为0则输出−1示例1
输入
复制
3
457 456 23输出
复制
478说明
小a有两种方法到达3号星球
第一种:1→2→3,最终耐久度为457⊕456⊕23=22
第二种:1→3,最终耐久度为457⊕23=478示例2
输入
复制
4
2 4 4 2输出
复制
-1示例3
输入
复制
5
234 233 123 2333 23输出
复制
253备注:
1⩽n,∀pi⩽3000#include
#include
#include
#include
#include
#include
#include
#include
#define Swap(a,b) a ^= b ^= a ^= b
using namespace std ;
const int MAX = 3005;
const int inf = 0xffffff;
const int mod = 1e9+7 ;
typedef long long LL;
int minn = 0x3f3f3f3f ;
LL maxx = -0x3f3f3f3f;
// --------------------------------
LL gcd(LL a , LL b)
{
return b== 0 ? a : gcd(b,a%b) ;
}
int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int dp[MAX] ;
int a[MAX] ;
int main()
{
int n ;
n = read() ;
for(int i = 1 ;i <=n ; i++ )
{
a[i] = read() ;
dp[i] = -1;
}
dp[1] = a[1] ;
for(int i = 1 ;i<=n ; i++ )
{
for(int j = 1 ; j<=n; j++ )
{
if(i == j)
continue ;
else
{
if(a[j]>a[i])
dp[i] = max(dp[i],dp[j]^a[i]);
}
}
}
if(dp[n] !=-1)
{
cout<
小a与黄金街道
链接:https://ac.nowcoder.com/acm/contest/317/D
来源:牛客网
题目描述
小a和小b来到了一条布满了黄金的街道上。它们想要带几块黄金回去,然而这里的城管担心他们拿走的太多,于是要求小a和小b通过做一个游戏来决定最后得到的黄金的数量。
游戏规则是这样的:
假设道路长度为nn米(左端点为0,右端点n),同时给出一个数k(下面会提到kk的用法)
设小a初始时的黄金数量为AA,小b初始时的黄金数量为B
小a从1出发走向n−1,小b从n−1出发走向1,两人的速度均为1m/s
假设某一时刻(必须为整数)小a的位置为xx,小b的位置为yy,若gcd(n,x)=1且gcd(n,y)=1,那么小a的黄金数量AA会变为A∗kx(kg),小b的黄金数量BB会变为B∗ky(kg)
当小a到达n−1时游戏结束
小a想知道在游戏结束时A+B的值
答案对109+7取模
输入描述:
一行四个整数n,k,A,B输出描述:
输出一个整数表示答案示例1
输入
复制
4 2 1 1输出
复制
32说明
初始时A=1,B=1
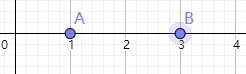
第一个时刻如图所示,小a在11,小b在33,满足条件,此时A=1∗21=2,B=1∗23=8
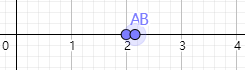
第二个时刻小a在22,小b在22,不满足条件
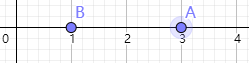
第三个时刻小a在33,小b在11,满足条件,此时A=2∗23=16,B=8∗21=16
此时游戏结束A=2∗23=16,B=8∗21=16
A+B=32
示例2
输入
复制
5 1 1 1输出
复制
2备注:
保证3⩽n⩽108,1⩽A,B,k⩽1013
题解:
#include
#include
#include
#include
#include
#include
#include
#include
#define Swap(a,b) a ^= b ^= a ^= b
using namespace std ;
typedef long long LL;
const int MAX = 3005;
const int inf = 0xffffff;
const LL mod = 1e9+7 ;
int minn = 0x3f3f3f3f ;
LL maxx = -0x3f3f3f3f;
// --------------------------------
LL gcd(LL a , LL b)
{
return b== 0 ? a : gcd(b,a%b) ;
}
LL power(LL a , LL b ,LL mod )
{
LL ans = 1 ;
while(b){
if(b&1)
ans = ans*a %mod ;
a = a *a %mod ;
b>>=1 ;
}
return ans ;
}
int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
LL eular(LL n){
LL ret=1,i;
for (i=2;i*i<=n;i++)
if (n%i==0){
n/=i,ret*=i-1;
while (n%i==0)
n/=i,ret*=i;
}
if (n>1)
ret*=n-1;
return ret;
}
int main()
{
LL n , k , a , b ;
cin >>n >> k >> a >>b ;
LL s = eular(n)/2 ;
LL res = power(k,s*n,mod) ;
printf("%lld",(a+b)* res%mod );
return 0;
}