方格取数（N = 2），多进程DP

方格取数还有N = 3 的情况，其实只要明白了N = 2 的情况，N = 3 的情况也会明白的。

转自：洛谷，作者: Lyrics 更新时间: 2017-10-02 08:41；

洛谷p1004

下面是题目描述：

设有 N × N 的方格图 (N ≤ 9) ，我们将其中的某些方格中填入正整数，而其他的方格中则放入数字 0 。如下图所示（见样例）:

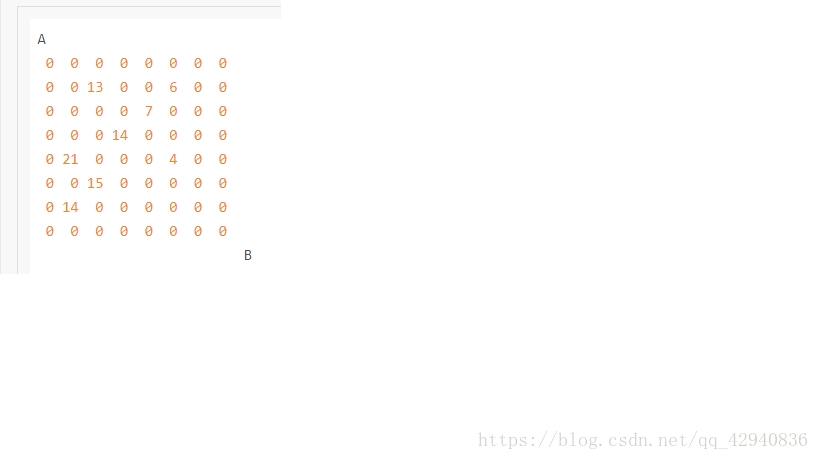
某人从图的左上角的 A 点出发，可以向下行走，也可以向右走，直到到达右下角的 B 点。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字 00 ）。
此人从 A 点到 B 点共走两次，试找出 2 条这样的路径，使得取得的数之和为最大。

输入输出格式

输入格式：

输入的第一行为一个整数 NN （表示 N \times NN×N 的方格图），接下来的每行有三个整数，前两个表示位置，第三个数为该位置上所放的数。一行单独的 0 表示输入结束。

输出格式：
只需输出一个整数，表示 2 条路径上取得的最大的和。

输入输出样例
输入样例#1：
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
输出样例#1：
67
说明
NOIP 2000 提高组第四题

题解：

我们做题的思路可以这样：

①先看一下出题日期（毕竟是NOIP的题目，有一定的水准），然后发现是2000年的普及第四题

我们要知道的是，好像比较前面的几年由于1999的数塔IOI问题后，接下来几年的最后一两题都很喜欢出DP

所以，我们首先看一下题目的内容，求路径最大的方法，这时候就要想到DP或者DFS

②然后我们发现题目的数据规模不大，n<=9，所以我们可以考虑用DFS或者DP都可以

但是鉴于 “好像比较前面的几年由于1999的数塔IOI问题后，接下来几年的最后一两题都很喜欢出DP “

我们觉得用DP会比较好

③而且，NOIP的压轴DP题你想要2维过（在考场上是很难想出来的）

所以我们考虑高维

④我们找到一个东西叫做四维DP，因为这题是两个人走，我们思考一下能不能单纯用两个人的模拟过呢？

显然是可以的，我们记f[i][j][k][l]表示第1条路线的i,j走法和第2条路线的k,l走法

显然我们可以两个人一起走，复杂度最多就是9*9*9*9=6561（哈哈哈时间复杂度这么低）

所以我们就用这个方法了！

⑤然后我们思考动归方程的写法：

第1条路线只可能是从i-1,j或者i,j-1转移，第2条路线也只可能从k-1,l或者k,l-1转移

而且因为是2个人走，如果走到一点我们的那个点就要打标记说那点上面的值为0

所以我们得到了我们的动归方程（注意：万一 i , j 与 k , l 相同这是要小心的！）

f [ i ][ j ][ k ][ l ] = max (f [ i - 1 ][ j ][ k - 1 ][ l ] , f [ i ][ j - 1 ][ k - 1 ][ l ] , f[ i - 1 ][ j ][ k ][ l - 1 ] , f[ i ][ j - 1 ][ k ][ l - 1 ])+a [ i ][ j ]+a [ k ][ l ];

补充：如果 i，j 和 k ， l 相同的话就需要减去一次当前的 a [ i ，j] 因为它被重复计算了 2 次，也就是 i == k ，j == l 的情况。

下面是作者的代码：

#include
using namespace std;
int n,x,y,val,ans=0,maxn,f[12][12][12][12],a[12][12];//a[i][j][k][l]表示两个人同时走，一个走i,j 一个走k,l 
int main(){
    scanf("%d",&n);
    memset(a,0,sizeof a);
    while(1){
        scanf("%d%d%d",&x,&y,&val);
        if(x==0&&y==0&&val==0)break;
        a[x][y]=val;
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            for(int k=1;k<=n;k++){
                for(int l=1;l<=n;l++){
                    f[i][j][k][l]=max(f[i-1][j][k-1][l],max(f[i][j-1][k-1][l],max(f[i-1][j][k][l-1],f[i][j-1][k][l-1])))+a[i][j]+a[k][l];
                    if(i==k&&j==l)f[i][j][k][l]-=a[i][j];
                }
            }
        }
    }
    printf("%d\n",f[n][n][n][n]);
    return 0;
}

这是我的代码：

#include 
#include 

using namespace std;

int f[10][10][10][10];
int a[10][10];

int main()
{
    ios::sync_with_stdio(false);
    int n;
    int x,y,number;
    int t,t2;
    cin >> n;
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= n; ++j)
            for (int k = 1; k <= n; ++k)
                for (int l = 1; l <= n; ++l)
                 f[i][j][k][l] = 0;
    while (1)
    {
        cin >> x >> y >> number;
        if (x == 0 && y == 0 && number == 0)
         break;
        a[x][y] = number;
    }
    for (int i = 1; i <= n; ++i)
    {
        for (int j = 1; j <= n; ++j)
        {
            for (int k = 1; k <= n; ++k)
            {
                for (int l = 1; l <= n; ++l)
                {
                    t = max(f[i - 1][j][k - 1][l],f[i][j - 1][k - 1][l]);
                    t2 = max(f[i - 1][j][k][l - 1],f[i][j - 1][k][l - 1]);
                    f[i][j][k][l] = max(t,t2) + a[i][j] + a[k][l];
                    if (i == k && j == l)
                     f[i][j][k][l] = f[i][j][k][l] - a[i][j];
                }
            }
        }
    }
    cout << f[n][n][n][n];
    return 0;
}