传送门
A.Adrien and Austin：
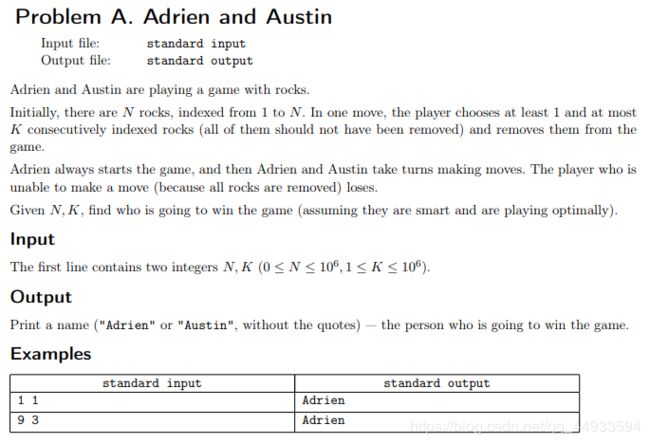
题意：
n个石子排成一列，每次能拿走最少一个最多k个（连续的没被拿走的），谁没石子拿谁输，输出获胜的人的名字，Adrien先手。
思路：
特判 k == 1和n == 0的情况，当k等于1时每次只能拿走1个，此时判断n的奇偶性，n为奇数时后手获胜，n为偶数时先手获胜；当n == 0时后手获胜，其余情况先手必胜。因为先手只需要拿走石子的最中间一个或者两个，拿走之后让分成两行的石子数量保持一致即可，此时不论后手在任何一边拿任何数量的石子，先手都可以镜像的在另一边拿，直到后手没有石子可拿。
AC代码：
/*---------------------------------
*File name: A.cpp
*Team: 这题太简单啦
*Author: Snpilola
*Creation date: 2019-10-04 12:00
*-------------------------------*/
#include
J.Prime Game：
题意：自己看题。
思路：计算所有质因子出现的位置压入vector中。计算每一个位置上的质因子对答案的贡献，即当前这个质因子作为答案出现的次数。
以样例2为例：可以得到如下表格：
| 下标 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
 |
6 |
7 |
5 |
5 |
4 |
9 |
9 |
1 |
8 |
12 |
| 质因子 |
2,3 |
7 |
5 |
5 |
2 |
3 |
3 |
|
2 |
2,3 |
将质因子压入vector中得到如下表格：
| 2 |
1 |
5 |
9 |
10 |
| 3 |
1 |
6 |
7 |
10 |
| 5 |
3 |
4 |
|
|
| 7 |
2 |
|
|
|
计算每个位置上的质因子对答案贡献：
pos = 1：2有贡献的区间为(1,1),(1,2),(1,3)......(1,10). 共10次。
3有贡献的区间为(1,1),(1,2),(1,3)......(1,10). 共10次。
pos = 2：7有贡献的区间为(2,2),(2,3)......(2,10)
(1,2),(1,3)......(1,10)共2 * 9次。
pos = 3：5有贡献的区间为(3,3),(3,4)......(3,10)
(1,3),(1,4)......(1,10)
(2,3),(2,4)......(2,10)共3 * 8次。
pos = 4：5有贡献的区间为(4,4),(4,5)......(4,10)
由于(1,4),(1,5)..... (2,4),(2,5)......., (3,4),(3,5)......的区间中5作为答案的贡献是从pos=3中的5来的，因此pos=4的5作为答案的贡献只有7次。
以此类推得出所有的位置上的值的贡献: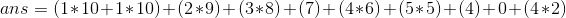
。
可以发现当前这个位置 
上的质数对答案的贡献为![\sum (n - vector[i][j]]+1)\times (vector[i][j] - vector[i][j - 1])](http://img.e-com-net.com/image/info8/8fe7f85ad800416b8e14314629d78178.gif)
。
当这个位置上的质数是这个质数第一次出现的位置时对答案的贡献为![(n-vector[i][0]+1)\times vector[i][0]](http://img.e-com-net.com/image/info8/6231038d6216480cb1a0799c80c0f43b.gif)
。
欧拉筛法线性筛出质数之后对每个质数在O（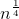
）的复杂度下分解质因子并将质因子的位置压入对应质数的vector中。
最后循环遍历出现的所有质数并且算出当前质数对答案的贡献求和。
AC代码：
/*---------------------------------
*File name: A.cpp
*Team: 这题太简单啦
*Author: Snpilola
*Creation date: 2019-10-04 12:00
*-------------------------------*/
#include
