2019春季选拔赛第一场A、B、C三题题解

菜是原罪。
比赛链接：2019春季SMUACM省赛预备队员选拔赛 - 第一场

题意：给出X，Z，求最小整数Y使得LCM（X, Y）= Z。
思路：求出x和z的gcd，然后以此gcd为基，每次+=gcd，直到当前答案和X的最小公倍数等于Z，输出-1的情况只有一种就是X不是Z的因子。
反思：很简单的一道题，但因为没有开LL一直WA，快吐了，结束之后全改LL立刻AC。
AC代码：

#include

long long gcd(long long x, long long y){
	if(y == 0) return x;
	while(1){
		long long pos = x;
		if(y == 0) return x;
		x = y;
		y = pos % x;
	}
}
long long lcm(long long x, long long y){
	return x * y / gcd(x, y);
}

int main(){
	long long x, z, m;
	scanf("%lld", &m);
	while(m--){
		scanf("%lld %lld", &x, &z);
		if(z % x != 0) {
			printf("-1\n");
			continue;
		}
		long long pos = gcd(x, z);
		long long y = (z / pos) / (x / pos);
		for(long long i = y; i <= z; i += y) {
			if(lcm(i, x) == z){
				printf("%lld\n", i);
				break;
			}
		}
	}
	return 0;
}

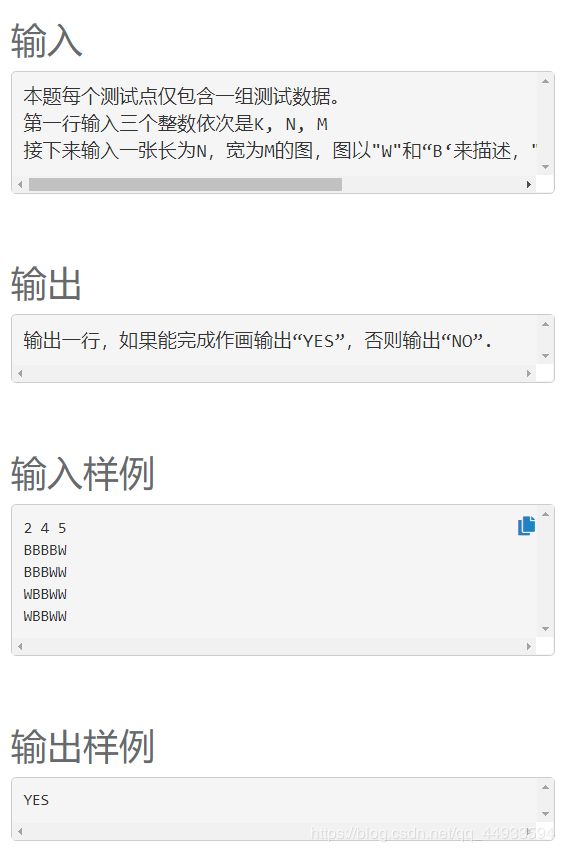
题意：如图。
思路：正难则反只需要一步一步倒推回去看看是否能够将画板还原成最初始的样子（没有B也没有W）。遍历每一个点，如果当前点所在的k*k的方块中只有单一种颜色，则可以将其全部转化成无色（用‘?’表示）。
反思：思路不够宽，强扭的瓜不甜，强做的题会错。
AC代码：

#include
#include
#include
#include
#include
using namespace std;

char a[25][25];
bool flag;
int k, m, n;

void solve(int x, int y){
	int cntw = 0, cntb = 0;
	for(int i = x; i <= x + k - 1; i++){
		for(int j = y; j <= y + k - 1; j++){
			if(a[i][j] == 'B' || a[i][j] == '?'){
				cntb++;
			}
			if(a[i][j] == 'W' || a[i][j] == '?'){
				cntw++;
			}
		}
	}
	if(cntb == k * k || cntw == k * k) {
		for(int i = x; i <= x + k - 1; i++){
			for(int j = y; j <= y + k - 1; j++){
				a[i][j] = '?';
			}
		}
	}
}

int main(){
	scanf("%d %d %d", &k, &n, &m);
	for(int i = 1; i <= n; i++){
		scanf("%s", a[i] + 1);
	}
	for(int time = 1; time <= 100; time++){//其实不用这么多，但既然时间复杂度允许就干脆多来几遍
		for(int i = 1; i <= n; i++){
			for(int j = 1; j <= m; j++){
				solve(i, j);
			}
		}
	}
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= m; j++){
			if(a[i][j] != '?') flag = 1;
		}
	}
	if(flag) printf("NO\n");
	else printf("YES\n");
	return 0;
}

题意：给出X求由01组成的为X的倍数的数。
思路：因为数据肯定会很大，必爆LL，所以当前答案得用字符串存，而要判断是否能够整除X，就需要对X求余，并且记录下此余数，如果之后的数再次出现此余数就不需要接着判断。如果当前数对X求余的结果没有出现过则把当前数加入队列中，直到余数为0。因为是01字符串，所以其实是前一个数乘10或前一个数乘10 + 1，新的数的余数则等于前一个数的余数乘10或乘10 + 1。只需要用结构体存储01字符串和此字符串对X的求余结果就ok了。
算法：BFS，每次在当前字符串之后加0或者1，判断余数，根据余数选择加入队列或不加入队列或输出答案。
反思：补题的时候出现了一点小差错，把结构体内的字符串开到了1e5，导致MLE，其实不需要1E5，甚至应该是不需要100的。

AC代码：

#include
#include
#include
#include
#include
#include
using namespace std;

int x;
struct NODE{
	char s[100];
	int ans;
};
queue<NODE> q;
bool mp[(int)1e6 + 5];

void bfs(){
	NODE flag;
	flag.s[1] = '1';
	flag.s[2] = '\0';
	flag.ans = 1 % x;
	q.push(flag);
	while(!q.empty()){
		NODE now = q.front();
		q.pop();
		mp[now.ans] = 1;
		int len = strlen(now.s + 1);
		NODE nex;
		/*0*/nex.s[len + 1] = '0';
			 nex.s[len + 2] = '\0';
			 for(int i = 1; i <= len; i++) nex.s[i] = now.s[i];
			 nex.ans = now.ans * 10 % x;
			 if(nex.ans == 0){
				 printf("%s\n", nex.s + 1);
				 return;
			 }
			 if(!mp[nex.ans]) q.push(nex);
		/*1*/nex.s[len + 1] = '1';
			 nex.s[len + 2] = '\0';
			 for(int i = 1; i <= len; i++) nex.s[i] = now.s[i];
			 nex.ans = (now.ans * 10 + 1) % x;
			 if(nex.ans == 0){
				 printf("%s\n", nex.s + 1);
				 return;
			 }
			 if(!mp[nex.ans]) q.push(nex);
	}
}

int main(){
	scanf("%d", &x);
	bfs();
	return 0;
}

剩余的两题有点不太明白，暂时不补了，以后要是想起来了再回来填坑qwq。